Измерение тесноты связи между атрибутивными признаками.

Коэффициент взаимной сопряженности Чупрова.

Для измерения тесноты связи согласованного варьирования атрибутивных варьирующих признаков применяются различные показатели, наиболее общим из них является коэффициент взаимной сопряженности Чупрова. Он применяется для сопряжения связи двух атрибутивных признаков, когда это варьирование образует 3 и более группы.

Пример, распределение 500 студентов заочников по оценкам на экзамене и характеру работы.

Характер работы Оценки	По специальности	Не по специальности	Итого
Отлично
(в квадрате)			0,15
(делим на итог)	7,1429	4,1666	11,3095
Хорошо
(в квадрате)			0,30
(делим на итог)	34,5714	10,6666	45,238
Удовлетворительно
(в квадрате)			0,492
(делим на итог)	92,5714	28,1666	120,738
Неудовлетворит.
(в квадрате)			0,0984
(делим на итог)	0,2857	2,6666	2,9523
Итого

1,0436 – эта сумма за вычетом единицы называется показателем взаимной сопряженности и обозначается 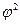, тогда коэффициент Чупрова рассчитывается:

,

где m – число групп по каждому признаку.

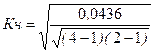=0.1587

Кч изменяется от 1 до 0, но уже при значении 0,3 можно судить о тесной связи между вариацией изучаемых признаков.

Коэффициент ассоциации.

Если вариация обоих атрибутивных признаков ограничена двумя группами, то коэффициент Чупрова может быть определен проще, в виде коэффициента ассоциации. Для этого исходные данные сводятся в комбинированную четырех клеточную таблицу.

	a	b	a + b
	c	d	c + d
	a + c	b + d

Ка рассчитывается по формуле:

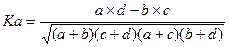
Пример, распределение населения на городское и сельское по переписям.

Место жительства	39 г.	70 г.	89 г.
г	н/г		г	н/г		г	н/г
Город	80,9	19,1		93,8	6,2		99,8	0,2
Село	50,6	49,4					99,5	0,5
	131,5	68,5		177,8	22,2		199,3	0,7

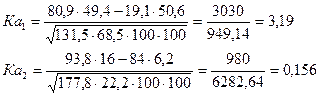
Ка изменяется от –1 до +1. Чем ближе он к крайним значениям, тем сильнее связаны между собой изучаемые признаки.