Вероятностный подход к определению риска
Вероятностные задачи характеризуются тем, что эффективность принимаемых решений зависит не только от детерминированных факторов, но и от вероятности их появления, то есть известен закон распределения управляемых факторов х в виде:
х1 х2 хn
p1 p2 pn
p – вероятность возникновения случайной величины.
Этой паре соответствует функция эффективности, выраженная через E(xi, pi).
В качестве функции эффективности может выступать математическое ожидание Е, дисперсия, СКО и коэффициент вариации.
Эффективность или математическое ожидание определяется по формуле: Е = S(xi × pi).
Дисперсия: Д = S(xi - Е)2 × pi
Сигма: 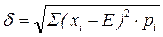
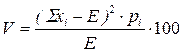
Величина Е представляет собой обобщенную количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала.
Чаще всего оценка рискованности производится с помощью СКО d2 (сигмы), означающей абсолютный риск.
Требуется сравнить по риску вложения в акции 3-х типов А, В, С. Если каждый из них по своему откликается на возможные рыночные ситуации, достигая с известными вероятностями определенных значений доходности.
| Тип акции | Ситуация 1 | Ситуация 2 | |||
| вероятность pi | доходность x | вероятность | доходность | ||
| А В С | 0,5 0,99 0,7 | 15,01 | 0,5 0,01 0,3 | 5,1 |
ЕА = 0,5×20 ± 10 + (0,5×10) = 15
ЕВ = 0,99×15,1 = 14,95 + (0,01×5,1) = 15
ЕС = 0,7×13 + 0,3×7 = 9,1 + 2,1 = 11,2
ДА = (20-15)2 ×0,5 + (10-15) ×0,5 = 12,5 + 12,5 = 25
ДВ = (15,1-15)2×0,99 + (5,1-15)2×0,01 = 0,01 + 0,98 = 0,99
ДС = (13-11,2)2×0,7 + (7-11,2)2×0,3 = 2,268 + 5,292 = 3
хА = 20 + 10 / 2 = 15 хВ = 15,1 +5,1 / 2 = 10,1 хС = 13 + 7 / 2 = 10
dА = Ö25 = 5 dВ = Ö0,99 = 0,99 dС = Ö3 = 1,75
VА = 167% VВ = 6,6% VС = 67,5%
Вывод:
По среднему значению доходности доминирующее выражение у акции А (15%), но по показателям абсолютной величины риска и коэффициент вариации доминирующее положение у В.
Дата добавления: 2015-12-26; просмотров: 995;
