Основные положения теории прочности деталей авиационных ГТД

Работоспособность элементов конструкции (деталей) авиационных ГТД (как и любых других инженерных конструкций) определяется:

- прочностью;

- жесткостью;

- устойчивостью.

Прочность конструкции или ее элементов – способность работать без разрушения под действием расчетных нагрузок.

Жесткость конструкции – свойство конструкции сопротивляться деформированию, т. е. изменению размеров и формы под действием нагрузок.

Устойчивость – способность конструкции сохранять свою первоначальную форму под действием расчетных нагрузок.

Для рассмотрения свойств конструкционных материалов в классической теории прочности используется модель твердого деформируемого тела, для которой считаются справедливыми следующие основные гипотезы:

1. Сплошность;

2. Однородность;

3. Изотропность;

4. Упругая деформируемость.

Ни одна из приведенных гипотез в чистом виде, строго говоря, не выполняется. Тем не менее, на базе такой сравнительно простой модели, которая явно чрезмерно идеализирует реальность, удалось разработать надежные методы расчета инженерных конструкций, испытывающих статические нагрузки. Любое твердое тело под действием внешней нагрузки деформируется. Если деформация полностью исчезает после устранения нагрузки – то она называется упругой, а соответствующие свойства тела восстанавливают свои размеры и формы – упругостью.

Если после снятия нагрузки деформация исчезает не полностью, то ее называют пластической, а соответствующие свойства тела – пластичностью.

Понятие напряжения

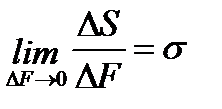
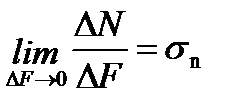– нормальное напряжение

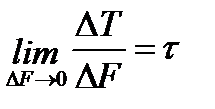– касательное напряжение

[σ_n] = Н/м² = Па

[τ_n] = Н/м² = Па

Для того чтобы иметь полное представление о напряжениях, действующих в окрестности рассматриваемой точки, необходимо выделить вокруг нее бесконечно малый объем, увязав его формулу с принятой системой координат.

Для декартовой системы координат это будет куб с гранями, параллельный координатным плоскостям. Напряженное состояние выбранной точки тела исчерпывающим образом характеризуется нормальными и касательными напряжениями σ_x, σ_y, σ_z – нормальные напряжения в направлении осей x, y, z. Касательное напряжение, вектор которого находится в плоскости, перпендикулярной оси обозначенной первой буквой индекса и направленная в сторону оси, обозначенной второй буквой индекса.

Касательные напряжения обладают свойством парности:

τ_xz = τ_zx ; τ_yx = τ_xy ; τ_zy = τ_yz.

Как правило, прочностной расчет детали стремятся построить так, чтобы одна из осей системы координат совпадала с направлением действия максимальных напряжений. Если это удастся, то напряжениями, действующими по другим осям – пренебрегают, и закон Роберта Гука приобретает простейшую формулу:

σ = Е ∙ ε,

где Е – модуль упругости первого рода (модуль Юнга), [Н/м²],

ε – относительная деформация. ε = ∆L / L₀.

Если напряжениями, действующими по другим осям пренебречь нельзя, то закон Гука усложняется.

Для двумерного напряженного состояния (тонкий диск, вращающийся с большой угловой скоростью) нужно записать:

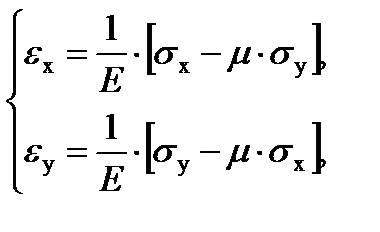
где ε_x, ε_y – относительные деформации в направлении осей

σ_x, σ_y – нормальные напряжения в направлении осей x, y;

Е – модуль Юнга;

μ – коэффициент Пуассона (коэффициент поперечной деформации). μ ≈ 0,3.

Закон Гука для трехмерного напряженного состояния:

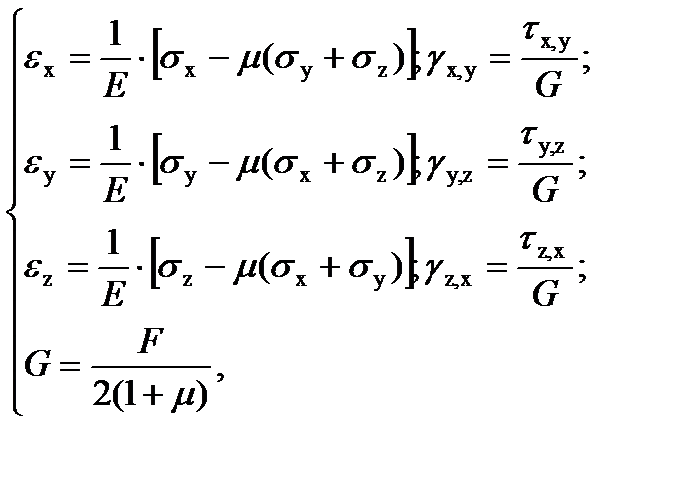
где ε_x, ε_y, ε_z – относительные деформации в направлении осей x, y, z;

γ_x,y, γ_y,z, γ_z,x – деформации сдвига в плоскостях, параллельных плоскостям xy, yz, zx;

τ_xy, τ_yz, τ_zx – касательные напряжения в соответствующих плоскостях;

Е – модуль Юнга, характеризующий способность материала сопротивляться растяжению (сжатию);

G – модуль упругости второго рода (модуль сдвига), характеризующий жесткость материала при сдвиге;

μ – коэффициент поперечной деформации.