Спектральные характеристики сигнала изображения

Известно, что любой периодический сигнал можно представить в виде суммы гармонических составляющих с частотами, кратными частоте повторения сигнала:

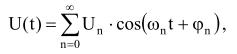
где U n – амплитуда, ω n – частота; ϕ n – начальная фаза «n» – гармонической составляющей; ω n = 2π n/Т, где Т – период повторения сигнала.

Гармонические составляющие называются спектральными составляющими, а само представление сигнала называется спектральным разложением сигнала U(t) (спектром сигнала). Отметим основные особенности спектра сигнала черно-белого изображения при чересстрочной развертке (рис. 1.8).

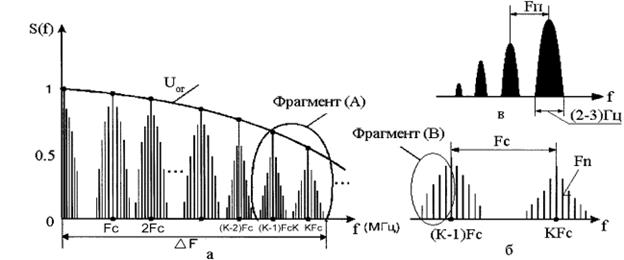
Рис. 1.8. Спектр сигнала черно-белого изображения: а – общий вид; б – фрагмент А в увеличенном масштабе; в – фрагмент В в увеличенном масштабе при движущемся объекте; U ог – огибающая спектра.

Величина спектральных составляющих сигнала убывает с ростом частоты.

Спектр сигнала изображения дискретный. Он содержит гармоники кF c

(где к = 1, 2, 3, …; Fс – частота повторения строк). Вокруг каждой гармоники кFс справа и слева группируются составляющие с частотами, отстоящими от нее на величину ± mFп (где m = 1, 2, 3,..; Fп – частота повторения полей).

Таким образом, спектр сигнала изображения состоит как бы из «сгустков» энергии на частотах, кратных частоте строк. Описанная структура обусловлена периодичностью сигнала изображения с частотой строк и полей.

Спектр сигнала изображения имеет составляющую на нулевой частоте.

4. Для воспроизведения формы сигнала изображения достаточно передать составляющие спектра от нулевой частоты до f max = ΔF.

При передаче движущегося объекта содержание каждого последующего изображения от кадра к кадру мало отличается от предыдущего, т.к. скорость смены кадров значительно больше скорости передвижения объекта по экрану. Однако перемещение объекта изменяет во времени амплитуды и фазы спектральных составляющих. Это приводит к тому, что вокруг каждой спектральной линии появляются составляющие настолько близко расположенные друг к другу, что спектральная линия вместе с этими составляющими образует непрерывный спектр, форма которого похожа на лепесток (рис. 1.8, в). Ширина таких

«лепестков» составляет единицы Герц и определяется скоростью движения изображения по экрану.