ПЛОСКАЯ СИСТЕМА СИЛ
Плоской называется такая система сил, линии действий которых расположены в одной плоскости. При рассмотрении плоской системы сил введем определения для нагрузок. Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело
(рис. 8).
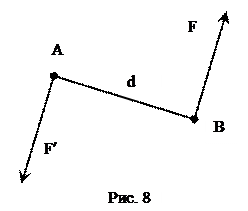 Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
действия другой называется плечом пары (d). Действие пары сил определяется моментом пары. Численное значение момента пары определяется как произведение модуля одной из сил на плечо этой пары.
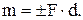
Приведем следующие два свойства пар сил:
1. Данную пару, не изменяя её действия на тело, можно переносить как угодно в плоскости её действия.
2. Не изменяя действия данной пары на тело, можно изменять модуль сил и плечо этой пары, сохраняя неизменным модуль и направление вращения пары.
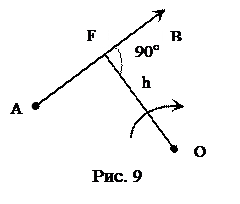 Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Mo(F)=±F∙h.
Момент силы считается положительным, если тело под действием данной силы стремится вращаться относительно точки О против часовой стрелки.
Отметим следующие свойства момента силы:
1. Момент силы относительно данной точки не изменяется при переносе точки приложения силы вдоль линии действия силы.
2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку.
При решении задач на плоскую систему сил пользуются уравнениями равновесия. Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма проекций этих сил на две координатные оси и сумма моментов относительно произвольно выбранной точки равнялись нулю
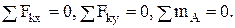
Существуют и две другие формы условий равновесия, но они используются гораздо реже.
Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось, не перпендикулярную к прямой АВ, были равны нулю.
Третья форма: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительной любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю.
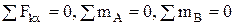 ;
;
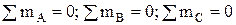 .
.
Задача 2
Лестница АВ длиной 2а и весом Р опирается на гладкий горизонтальный пол и 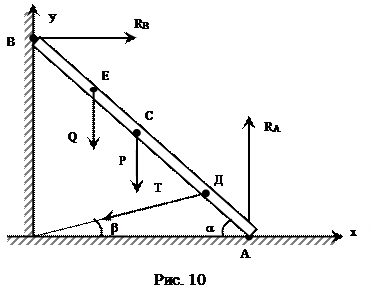 гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние
гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние 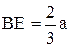 . Центр тяжести C лестницы находится в её середине (рис. 10).
. Центр тяжести C лестницы находится в её середине (рис. 10).
Решение: Используя принцип освобождаемости от связей, убираем связи, а их действие заменяем соответствующими реакциями. Составляем уравнения равновесия. Оси координат указаны на рис. 10.
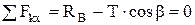 , (1)
, (1)
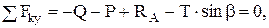 (2)
(2)
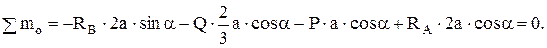 (3)
(3)
Из первого уравнения получаем: 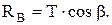
Из второго уравнения получаем: 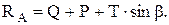
Подставляем значения для RA и RB в уравнение (3) и находим значение для
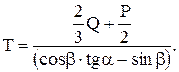
Задача 3
Определить опорные реакции в балочной конструкции, приведенной на
рис. 11, если Р=2 кН, q = 3 кН/м, m = 5 кНм. Размеры приведены на рис.11.
Решение: Используем принцип освобождаемости от связей, для чего вместо связей укажем их реакции (рис. 11, а). Указав оси координат для расчетной схемы, составляем уравнения равновесия. В данной задаче имеется три составляющих неизвестных опорных реакций, следовательно, необходимо составить три уравнения равновесия.
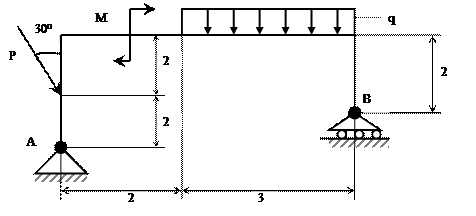

Рис. 11
Распределенная нагрузка, т.е. нагрузка приходящаяся на единицу длины, задается интенсивностью q= Н/см. Грузовая нагрузка, которая представляется как сосредоточенная сила равна Q=q∙ℓ, прикладывается в центре тяжести фигуры, образованной распределенной нагрузкой.
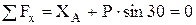 , (1)
, (1)
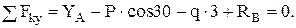 (2)
(2)
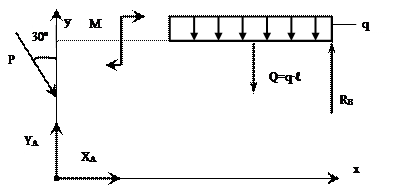

Рис. 11, а
При составлении третьего уравнения нужно учесть следующие два правила:
1. Момент от распределенной нагрузки равен, взятой с соответствующим знаком, площади грузовой нагрузки, умноженной на расстояние от центра тяжести грузовой нагрузки до рассматриваемой точки, относительно которой берется момент.
2. Если сила расположена под углом к координатным осям, то её необходимо разложить по проекциям на эти оси, а затем определять момент от каждой проекции в отдельности
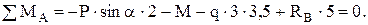 (3)
(3)
Момент следует брать относительно той точки, в которой сходятся большее количество неизвестных опорных реакций. Из полученных уравнений определяем неизвестные опорные реакции в следующем порядке:
из уравнения (3): 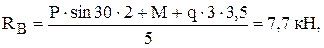
из уравнения (1): 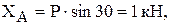
из уравнения (2): 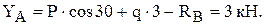
Следует отметить, что если при решении задач опорная реакция получилась со знаком минус, то, следовательно, её направление первоначально было выбрано неверно и его следует сменить на противоположное.
Дата добавления: 2015-12-26; просмотров: 6001;
