СИСТЕМА СХОДЯЩИХСЯ СИЛ
Сходящимися называются силы, если их линии действия пересекаются в одной точке. При решении задач на систему, сходящихся сил используются два способа: геометрический и аналитический. Геометрический метод основан на определении, что для уравновешенной системы сходящихся сил силовой многоугольник должен быть замкнутым.
В основу аналитического метода положено понятие проекции силы на ось. Проекцией силы на ось будем называть длину отрезка оси, заключенную между проекциями начала и конца данной силы на ось, взятую с соответствующим знаком (рис. 6).
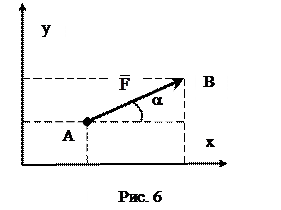 Из рис. 6 видно, что Fx = F∙ cos a,
Из рис. 6 видно, что Fx = F∙ cos a,
Fy = F∙sin a. Принимая во внимание, что для системы сходящихся сил, находящихся в равновесии, проекции равнодействующей на соответствующие координатные оси будут равны нулю, получаем аналитические условия равновесия системы:
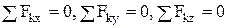 .
.
Задача 1
Однородная балка длины 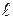 и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если
и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если 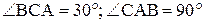 (рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
(рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
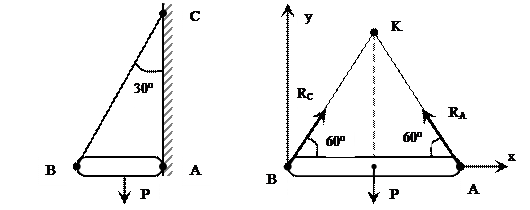

Рис. 7 Рис. 7, а
Геометрический метод.
Из сил, действующих на тело, строим силовой треугольник, который должен быть замкнутым, т.к. под действием этих сил тело находится в равновесии
(рис. 7, б). Для этого откладываем силы по известным направлениям, в любом выбранном масштабе.
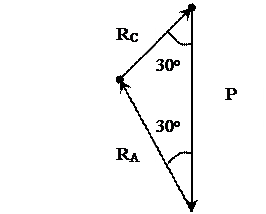 Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
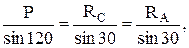
откуда получаем 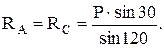
Рис. 7, б
Аналитический метод.
Для решения задачи составляются уравнения равновесия в виде суммы проекций всех сил на оси координат. Направления осей показаны на рис.7, а.
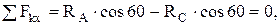 (1)
(1)
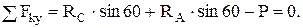 (2)
(2)
Из первого уравнения получаем RC =RA. Из второго находим 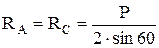 .
.
Дата добавления: 2015-12-26; просмотров: 839;
