Способы детальной разбивки закруглений
 Способ прямоугольных координат является наиболее точным и простым; он применяется в открытой равнинной местности. В этом способе положение точек на кривой через равные промежутки k определяется прямоугольными координатами х и y; за ось абсцисс принимают линию тангенса (касательной), а за начало координат — начало (НК) или конец кривой (КК).
Способ прямоугольных координат является наиболее точным и простым; он применяется в открытой равнинной местности. В этом способе положение точек на кривой через равные промежутки k определяется прямоугольными координатами х и y; за ось абсцисс принимают линию тангенса (касательной), а за начало координат — начало (НК) или конец кривой (КК).
Для вычисления координат х, у точек детальной разбивки предварительно вычисляют центральный угол θ, соответствующий заданной дуге k,
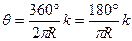
Далее, решая прямоугольный треугольник ОС1, получают:
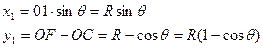
или 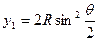
Аналогичным образом вычисляют координаты последующих точек, расположенных на первой половине кривой, через расстояние k по дуге кривой:
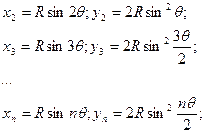
Определение положения точек 1, 2, 3, ... кривой на местности сводится к откладыванию рулеткой от НК (или КК) по направлению тангенса отрезков х1, х2, х3 …, построению при помощи эккера (теодолита) перпендикуляров из концов этих отрезков и откладыванию по ним отрезков у1, у2, у3 …,
 Разбивку ведут от начала кривой (НК) до середины, а затем от конца кривой (КК) также до середины кривой (СК). Обе половины кривой должны сомкнуться в точке СК, что контролирует точность детальной разбивки. Достоинством данного способа является то, что положение каждой точки кривой определяется независимыми промерами и при переходе от одной точки к другой погрешности не накапливаются.
Разбивку ведут от начала кривой (НК) до середины, а затем от конца кривой (КК) также до середины кривой (СК). Обе половины кривой должны сомкнуться в точке СК, что контролирует точность детальной разбивки. Достоинством данного способа является то, что положение каждой точки кривой определяется независимыми промерами и при переходе от одной точки к другой погрешности не накапливаются.
Полярный способ (способ углов) целесообразно применять на косогорах, насыпях и в полузакрытой равнинной местности. Способ базируется на положении геометрии о том, что угол с вершиной в какой-либо точке кривой, образованный касательной и секущей, равен половине соответствующего центрального угла. Как видно из рисунка, хорда 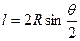 . Отсюда
. Отсюда 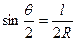 .
.
Положение точек кривой на местности определяют линейно-угловыми засечками. Для этого теодолит устанавливают в точке НК (или КК) и от направления тангенса откладывают последовательно углы 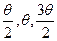 и т. д. Отложив рулеткой по направлению первого визирного луча отрезок l, закрепляют на местности точку 1. Из точки1 протягивают рулетку до пересечения отрезка l со вторым визирным лучом и закрепляют точку 2 и т. д.
и т. д. Отложив рулеткой по направлению первого визирного луча отрезок l, закрепляют на местности точку 1. Из точки1 протягивают рулетку до пересечения отрезка l со вторым визирным лучом и закрепляют точку 2 и т. д.
Недостатком способа является снижение точности детальной разбивки с увеличением числа точек, так как положение каждой последующей точки находится относительно предыдущей.
Способ продолженных хорд применяют при разбивке кривых на застроенных и залесенных участках, в выемках и тоннелях.
Разбивку кривой ведут с помощью мерной ленты и рулетки. По радиусу кривой R и принятой длине хорды l вычисляют длину отрезка d, называемого промежуточным перемещением.
 Значение величины d находят из подобия треугольников 0—1—2 и 1—2—2':
Значение величины d находят из подобия треугольников 0—1—2 и 1—2—2':
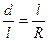 отсюда
отсюда 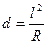
Положение первой точки кривой находят способом прямоугольных координат; при этом значения координат х1 и у1 вычисляют по формулам (1) и (2). Закрепив на местности точку 1, на продолжении створа линии НК—1 откладывают длину хорды l и отмечают временную точку 2'. Затем находят положение точки 2 на кривой линейной засечкой отрезками I из точки 1 и d из точки 2''. Положение остальных точек детальной разбивки до середины кривой находится аналогичным образом.
Данный способ имеет тот же недостаток, что и полярный способ.
Дата добавления: 2015-12-22; просмотров: 1159;
