Эквивалент реактивной мощности

Потери активной мощности в линии выражаются формулой

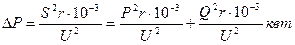, (2)

где S, Р, Q – кажущаяся, активная и реактивная нагрузки линии, ква, квт и квар; U – линейное напряжение, кв; r –активное сопротивление линии, ом.

Таким образом, суммарная потеря мощности может быть разбита на две составляющие:

потерю от активной нагрузки

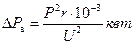(3)

и потерю от реактивной нагрузки

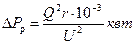. (4)

При уменьшении реактивной нагрузки – подключении у потребителя конденсаторов мощностью Q_С – активная нагрузка, а, следовательно, и DР_а практически остаются постоянными, потеря же от реактивной нагрузки уменьшается и становится равной:

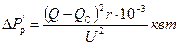. (5)

Снижение потери мощности, полученное в результате компенсации, равно:

. (6)

Наибольшее снижение потерь получается при Q_С=Q, т. е. при cosj₂=1. При дальнейшем увеличении Q_С снижение потерь уменьшается. Снижение потерь, приходящееся в среднем на 1 квар мощности конденсаторов, составит:

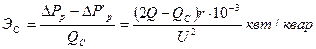. (7)

Э_С принято называть средним экономическим эквивалентом реактивной мощности.

Так как Q_С=cQ, то последнее выражение может быть представлено в следующем виде:

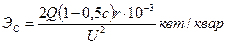.(8)

При увеличении степени компенсации от с=0 до c=1 абсолютная величина снижения потерь увеличивается, но одновременно уменьшается величина Э_С. При с ® 0 она достигает максимальной величины

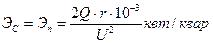, (9)

Э_п принято называть предельным экономическим эквивалентом, и им обычно пользуются для определения эффективности компенсации в различных звеньях электрической сети.

Заменив в уравнении (8) r на rl, получим следующее выражение Э_п для линий:

, (10)

где 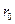- удельное сопротивление материала проводов ом×мм²/км;

l - длина линии, км;

s - сечение проводов линии, мм².

Обозначая 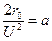, получаем:

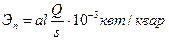. (11)

Для трансформаторов

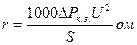, (12)

где DР_к.з. - потери короткого замыкания, квт;

S - номинальная мощность трансформатора, ква.

Подставив это выражение в уравнение (8), получим после преобразования:

, (13)

где b - степень загрузки трансформатора реактивной мощностью.