Гидродинамика течения

Поскольку интенсивность конвективного теплообмена напрямую зависит от гидродинамической обстановки вблизи поверхности, обсудим более подробно физику обтекания поверхности жидкостью не вникая в математические и физические подробности, т. к. эти вопросы относятся к компетенции таких дисциплин, как гидромеханика, аэродинамика, гидравлика и проч.

Во-первых, различают два режима течения жидкости: ламинарный и турбулентный; во-вторых, гидродинамическая обстановка зависит от побудительной причины течения. Одна из причин течения обусловлена силой Архимеда, возникающей в жидкости в поле массовых сил (в частности, в поле тяжести) в неизотермических условиях, когда более нагретые объёмы жидкости, имея мèньшую плотность, движутся вверх, а более холодные опускаются вниз. Возникающие при этом конвективные потоки носят название естественной (натуральной, свободной) конвекции. Вторая побудительная причина течения обусловлена действием внешних по отношению к потоку сил, создаваемых вентилятором, компрессором, насосом и т. д., и носит название вынужденной конвекции. Исходя из физического смысла критериев подобия легко видеть, что в случае естественной конвекции определяющим критерием будет критерий Грасгофа Gr, а в случае вынужденной конвекции, при которой скорости обтекания поверхности сравнительно велики, – критерий Рейнольдса Re. Это не значит, конечно, что критерий Грасгофа совершенно не играет роли в процессе вынужденной конвекции, так же как критерий Рейнольдса в процессе естественной конвекции, однако естественно считать, что в режиме развитой турбулентности естественная конвекция перестаёт играть какую-либо заметную роль, и наоборот, в отсутствие вынужденной конвекции, например, при малой скорости ветра, вынужденная конвекция как фактор интенсификации теплообмена пренебрежимо мала.

Как показали экспериментальные исследования течения (Осборн Рейнольдс, Англия) переход от ламинарного (lamina – пластинка) течения к турбулентному (turbulentus – бурный, беспорядочный) происходит практически мгновенно при практически одинаковых значениях безразмерного критерия для данной геометрии течения, получившего название критерия Рейнольдса. Такая ситуация представлена качественно на рис. II.I.1.

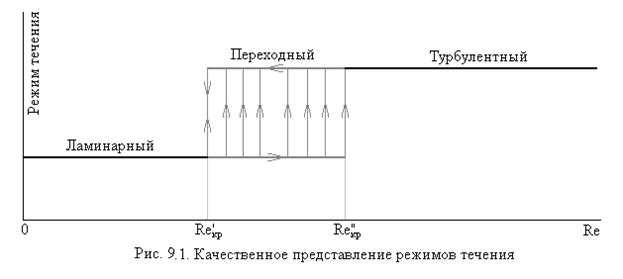
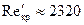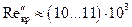В частности, при течении газов и жидкостей внутри труб и каналов и при продольном обтекании пучков труб критические числа Рейнольдса принимают приблизительные значения и . При других геометриях течения критические значения критерия Рейнольдса принимают другие значения.

Заметим, что представленная на рис.9.1 фигура по характеру своему напоминает петлю гистерезиса, известную в практике ферромагнетизма.

Приведём для справок некоторые результаты экспериментальных и теоретических исследований, касающихся чистой гидро- и аэродинамики обтекания твёрдых поверхностей в изотермическом и неизотермическом потоке жидкости.

Формула Пуазейля

При стабилизированном ламинарном течении в круглой трубе справедлив параболический закон распределения скоростей при течении несжимаемой вязкой жидкости с постоянными теплофизическими свойствами, а именно

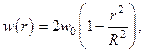
где w – расходная скорость жидкости; R – внутренний радиус трубы.

Расход жидкости в трубе цилиндрического сечения диаметром d при заданном перепаде давлений 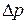на входе и на выходе из трубы при ламинарном режиме течения жидкости определяется формулой Пуазейля

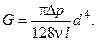
Формула Стокса

Сила гидродинамического сопротивления, оказываемого равномерному движению твёрдой сферы в несжимаемой жидкости описывается в первом приближении формулой Стокса

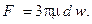
Гидродинамический пограничный слой

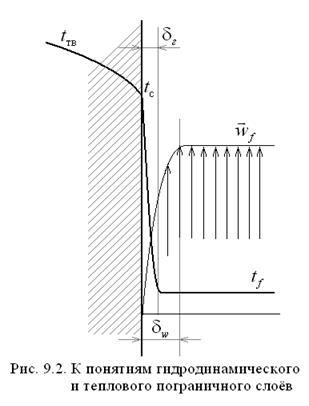
Визуальные наблюдения и приборные исследования показывают, что в боль-шинстве случаев обтекания жидкостью твёрдой поверхности (особенно если вяз-кость жидкости невелика) скорость потока существенно меняется в относительно тонком слое около поверхности, называ-емом гидродинамическим пограничным слоем 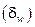(см. рис. 9.2).