Естественная конвекция в прослойках

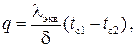
где

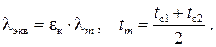
Здесь 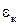– коэффициент конвекции, вычисляемый по критериальной формуле

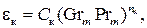
где значения множителя C_ки показателя степени n_кприведены в нижеследующей таблице. В качестве линейного размера выбирается толщина прослойки .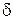

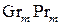
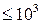
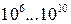
Cк		0.105	0.4
nк		0.3	0.2

Теплообмен при кипении жидкости в большом объёме

Кипением называется процесс парообразования при температуре, соответствующей температуре насыщения при заданном давлении, зависимость которой даётся уравнением Клапейрона–Клаузиуса в дифференциальной форме

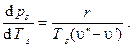
Здесь r – скрытая теплота парообразования, т. е. теплота, необходимая для превращения единицы массы кипящей жидкости в сухой насыщенный пар при постоянном давлении (температуре); 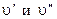– удельные объёмы кипящей жидкости и сухого насыщенного пара соответственно.

Для поддержания процесса кипения необходимо подводить непрерывно теплоту к жидкости в количестве M r, т.е. кипение всегда связано с теплообменом, При кипении паровая фаза образуется в виде пузырей. Так как подвод тепла осуществляется через поверхность теплообмена, то и пузыри возникают на этой поверхности. Если поверхность погружена в большой объём жидкости, вынужденное движение которой отсутствует, то такой процесс называют кипением в большом объёме.

Для возникновения кипения необходимо и достаточно два условия: наличие перегрева жидкости по сравнению с температурой насыщения при заданном давлении жидкости и наличие центров парообразования, в качестве которых могут выступать включения в жидкости (пыль, ионы, пузырьки газа), а также углубления и впадины на поверхности теплообмена, что связано с шероховатостью.

Пусть жидкость находится в сосуде с обогреваемым дном. Если жидкость кипит, то температура пара над жидкостью равна 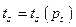. Температура в самой жидкости всегда несколько выше 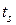. По мере приближения к обогреваемому дну температура t_ж практически не меняется.. Лишь в непосредственной близости от дна происходит её резкое увеличение до 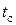. Здесь же находятся центры парообразования, т.е. пузыри образуются на поверхности теплообмена.

Если в образовавшемся пузыре давление пара больше давления, обусловленного наличием окружающей жидкости и силой поверхностного натяжения, то такой пузырь будет развиваться, т.е. увеличиваться в объёме за счёт испарения жидкости внутрь него. Объём пузыря будет увеличиваться до тех пор, пока подъёмные силы не превысят сил, удерживающих его на поверхности.

Размер пузыря в момент его отрыва характеризуется его отрывным диаметром d_s . Оторвавшийся пузырь перемещается кверху и, если жидкость перегрета, продолжает увеличиваться в объёме. На поверхности раздела «жидкость – пар» пузырь лопается. Так как пузыри возникают, растут и отрываются вблизи поверхности теплообмена, то они тем самым разрушают пограничный слой, который является основным термическим сопротивлением. Поэтому теплоотдача при кипении является высокоэффективным процессом. Для воды, например, коэффициент теплоотдачи α достигает значений 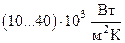. 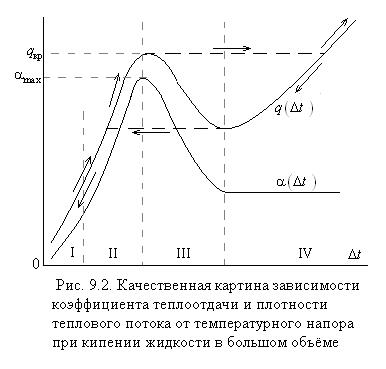В процессе кипения поверхность теплообмена контактирует частично с паровой, частично с жидкой фазами. Но поскольку теплопроводность жидкости значительно выше теплопроводности пара, т.е. 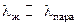, поэтому тепло передаётся в основном жидкой фазе, т.е. идёт на её перегрев, и лишь затем перегретая жидкость испаряется с поверхности пузырей внутрь их. С ростом перегрева жидкости всё меньшая шероховатость может служить центрами парообразования, а это приводит к увеличению их числа, и кроме того увеличивается частота отрыва пузырей в каждом центре парообразования. Это ведёт к возрастанию теплоотдачи. На рис. 9.2 приведена зависимость коэффициента теплоотдачи α и плотности теплового потока q от степени перегрева 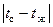. При этом можно выделить следующие режимы кипения. При небольших температурных напорах Δt теплоотдача определяется в основном условиями свободной конвекции, так как количество образующихся пузырей невелико и они не оказывают существенного влияния на пограничный слой (область конвективного кипения I). В области II наблюдается увеличение темпа роста коэффициента теплоотдачи α в связи с увеличением числа пузырей (область пузырькового кипения II ). С дальнейшим ростом температурного напора, т.е. разности температур между греющей поверхностью и нагреваемой жидкостью, число пузырей увеличивается настолько, что они начинают сливаться в паровую плёнку, что ухудшает условия теплообмена между греющей поверхностью и нагреваемой жидкостью (переходная область III). Далее возникает плёночный режим кипения (IV), в котором коэффициент теплоотдачи практически не зависит от температурного напора 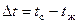, а тепловой поток линейно возрастает с увеличением в соответствии с определением . Чаще всего в энергетической практике режим кипения является пузырьковым. Расчёт теплоотдачи в этом режиме производится с помощью критериальных (эмпирических) уравнений. Несмотря на большое число факторов, влияющих на теплообмен при кипении в большом объёме, плотность теплового потока, а значит и коэффициент теплоотдачи α зависит в основном от физических свойств жидкости. Для воды (H₂O) эмпирические зависимости представляются в размерном виде

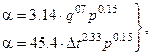
где входящие в эти выражения величины должны быть представлены в строго определённых размерностях, а именно

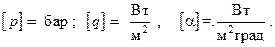
На рис.9.2 можно выделить так называемую петлю теплового гистерезиса, которая наблюдается, если тепловой поток q обусловлен только внешними причинами (например, электронагрев). Здесь имеет место так называемый кризис кипения.

Теплообмен при кипении жидкости, движущейся внутри труб

Этот процесс по сравнению с процессом кипения в большом объёме осложняется двумя факторами: ограниченностью объёма, в результате чего паровая фаза остаётся вблизи поверхности, и наличием вынужденного движения. Исследования показали, что если объёмное паросодержание не превышает 70…80 %, то его влиянием на теплопередачу можно пренебречь. Воздействие скорости вынужденного движения жидкости w проявляется по двум направлениям: во-первых, на возмущения в пограничном слое, вызванные процессом кипения, накладываются турбулентные вихри, связанные с вынужденным движением жидкости; во-вторых, в движущемся потоке отрыв пузырей происходит раньше, поэтому оба фактора приводят к увеличению теплоотдачи.

Теплообмен при конденсации пара на охлаждаемых поверхностях

Конденсацией называется процесс перехода вещества из парообразного состояния в жидкое.

Конденсация может происходить либо в объёме пара (в случае переохлаждения пара и наличия центров конденсации – пыли, ионов и т.д.), либо на поверхности с температурой ниже температуры насыщения пара при заданном давлении.

Известно, что конденсация пара, т. е. фазовый переход, происходит при постоянной температуре, если давление постоянно. Соотношение между температурой и давлением при фазовых переходах даётся формулой Клапейрона – Клаузиуса .

В теплообменных аппаратах – конденсаторах конденсация происходит на поверхностях, температура которых как правило ниже температуры пара в объёме. При этом конденсирующаяся жидкость покрывает поверхность, что в большой мере влияет на условия теплопереноса от пара к поверхности. Это влияние зависит также от картины течения конденсата на поверхности. Экспериментально наблюдаются два вида распределения конденсирующейся жидкости на поверхности: плёночная конденсация и капельная конденсация.

Плёночная конденсация наблюдает-ся тогда, когда жидкость смачивает твёр-дую поверхность (угол смачивания θ < 90^о), а капельная конденсация имеет место при угле смачивания θ > 90^о. Смачиваемость или несмачиваемость поверхности жидкостью зависит от рода, температуры и чистоты жидкости и от материала поверхности, её чистоты и обработки. В большинстве теплообменных аппаратов, если в них теплоносители не являются парами металлов, режим конденсации является плёночным, поэтому мы им займёмся подробно.

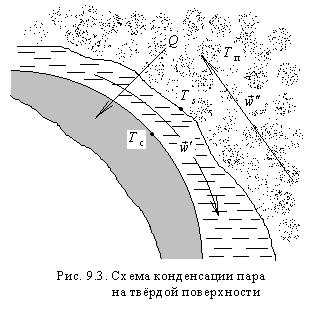
Плёнка конденсата, образующаяся на теплообменной поверхности, представляет собой термическое сопротивление, величина которого, кроме теплофизических свойств жидкости, зависит также от толщины плёнки, которая в свою очередь зависит от скорости конденсации и от возможности отвода конденсата с поверхности, что определяется её геометрией и ориентацией относительно направления поля тяжести или полей массовых сил. Схема задачи представлена на рис. 9.3.

Таким образом, тепловой поток, передаваемый от конденсирующегося пара к стенке, будет определяться тремя последовательно включёнными термическими сопротивлениями: а) от пара к поверхности плёнки конденсата; б) в плёнке конденсата; в) от конденсата к стенке. При этом температура пара T_п может быть выше температуры насыщения при данном давлении. Тогда температура стенки T_с должна быть меньше температуры насыщения T_s, чтобы конденсация имела место, т. е. T_п > T_s, T_с < T_s . С другой стороны, пар может содержать неконденсирующиеся примеси, которые затрудняют конденсацию. Далее, плёнка конденсата может течь со скоростью , а пар двигаться со скоростью 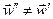, что будет приводить к их гидродинамическому воздействию и к возникновению пульсаций поверхности плёнки и т. д.

Подробный анализ экспериментальных данных показывает, что в широком диапазоне конструктивных и теплофизических параметров термическим сопротивлением от пара к поверхности конденсата и от конденсата к стенке можно пренебречь по сравнению с термическим сопротивлением плёнки конденсата, т. е. можно записать

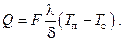
Поскольку толщина плёнки δ и температура стенки T_с являются в общем случае переменными на поверхности, более корректной будет запись в интегральной форме

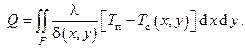
Задача вычисления этого интеграла в общем случае является безнадёжно сложной. Обычно её ставят следующим упрощённым способом (Нуссельт):

1) поверхность теплообмена является плоской, расположенной вертикально;

2) температура поверхности T_с постоянна;

3) теплофизические свойства пара и конденсата постоянны;

4) температура пара равна его температуре насыщения, т. е. T_п = T_s;

5) стекающая под действием силы тяжести плёнка конденсата движется ламинарно;

6) силы инерции в плёнке конденсата малы по сравнению с силами вязкого трения и тяжести;

7) вектор плотности теплового потока в плёнке направлен перпендикулярно к поверхности;

8) трение плёнки о пар отсутствует.

Тогда вектор плотности теплового потока будет иметь одну проекцию

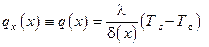
Величина 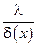при малой толщине плёнки 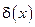может рассматриваться как коэффициент теплоотдачи

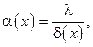
т. е.

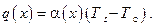
Таким образом, для расчёта теплового потока при конденсации пара необходимо знать толщину плёнки 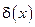. Расчёт толщины плёнки при принятых выше допущениях был дан в 1916 году Нуссельтом. Рассмотрим подробно классическую задачу Нуссельта (см. рис. 9.4). Через поперечное сечение плёнки с размером l = 1 м в направлении, перпендикулярном плоскости чертежа, протекает в единицу времени количество жидкости , где 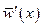– средняя по поперечному сечению плёнки скорость жидкости.

Пусть 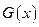– количество жидкости, образующееся на единичной поверхности в единицу времени на расстоянии x вследствие конденсации. Тогда баланс массы конденсата запишется следующим образом

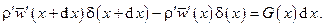
Разлагая функции 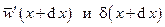в ряд Тейлора и ограничиваясь линейными членами разложения, получим

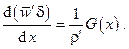
Причиной притока массы является конденсация пара, т. е. 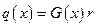, тогда с учётом получаем и принимает вид

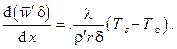
Это дифференциальное уравнение содержит две искомые функции 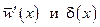. Средняя по сечению плёнки скорость конденсата может быть найдена с использованием уравнения Навье – Стокса

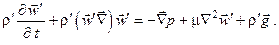
В стационарном случае в пренебрежении силами инерции и давления имеем для одномерного движения жидкости вдоль поверхности

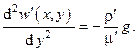
Здесь координата x, параллельная поверхности, выступает в роли параметра.

Граничные условия для этой задачи в принятых допущениях следующие:

Имеем тогда

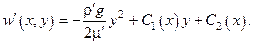
Из граничных условий получаем

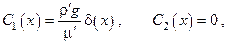
т. е.

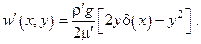
Средняя скорость в сечении x может быть рассчитана интегрированием

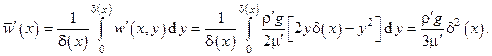
Уравнение для 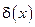принимает тогда вид

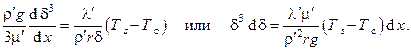
Решение этого уравнения есть

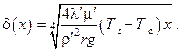
Для локального коэффициента теплоотдачи на расстоянии x от верхней кромки стенки получаем

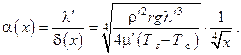
Средний по высоте H стенки коэффициент теплоотдачи

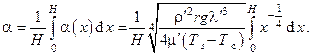
В результате интегрирования получаем

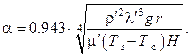
В этом выражении величины со штрихом представляют собой теплофизические свойства конденсата, которые следует брать по средней температуре плёнки 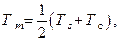а теплоту парообразования – по температуре насыщения пара.

Полученный результат может быть обобщён на наклонную стенку заменой

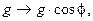
где 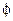– угол наклона стенки по отношению к вертикали. В связи с этим результат для α может быть перенесён на горизонтальную трубу усреднением по переменному углу 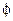, принимающему в этом случае значения от 0 до π. В результате получаем для горизонтальной круглой трубы

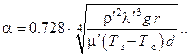
Влияние различных факторов на коэффициент теплоотдачи при конденсации пара

1. Полученные формулы для вычисления коэффициента теплоот-дачи при конденсации пара справедливы в случае неподвижного или медленно движущегося пара (< 10 м/с).

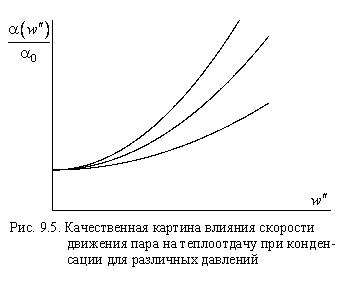Движение пара вызывает срыв плёнки, что приводит к уменьшению её толщины. Влияние скорости пара обычно даётся графически и качест-венно имеет вид, показанный на рис.9.5.

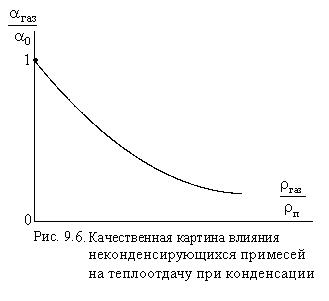
1. Неконденсирующиеся газы в паровой фазе, затрудняя подход пара к жидкой плёнке, уменьшают теплоотдачу, причём весьма сильно. Например, содержание газа в паре, равное по объёму 1 %, может снизить коэффициент теплоотдачи на 60 %. Обычно влияние неконденсирующихся газов в паре на коэффициент теплоотдачи задаётся также в виде графика (см. рис. 9.6).

2. Влияниеориентации и компоновкитеплообменных поверхностей конденсатора. Из уже полученных результатов ясно, что при горизонтальном расположении труб теплообменника коэффициент теплоотдачи выше, чем при вертикальном их расположении.

В самом деле, как следует из и 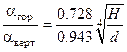, т. е. при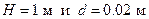 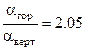. Увеличение коэффициента теплоотдачи объясняется тем, что эффективная (средняя) толщина плёнки при горизонтальном расположении труб меньше, чем при вертикальном. В 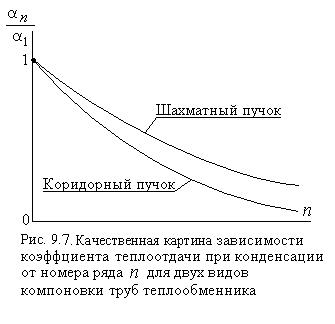случае же пучков труб более благо-приятным расположением является шахматное, так как при этом трубы в вертикальном ряду расположены реже, чем в коридорном пучке, и в среднем верхние ряды труб влияют меньше. Это влияние вызвано стеканием конденсата с верхних труб на нижние и представляется графически в виде, показанном качественно на рис. 9.7.

В заключение отметим, что на теплоотдачу при конденсации влияют также:

– перегрев пара;

– шероховатость поверхности;

– смесь различных конденсирующихся паров вместо чистого пара.

[1] В современной научной и технической литературе жидкости (в обычном понимании этого слова) и газы объединяют одним понятием «жидкость» в смысле сплошной текучей среды (флюид – fluide). При этом истинную жидкость называют «капельная жидкость», а газы (и пары) – «некапельная жидкость».