Общие сведения о приборах СВЧ. Виды приборов

Общие сведения о приборах СВЧ. Электронные приборы диапа­зона сверхвысоких частот имеют ряд особенностей, отличающих их от обычных электронно-управляемых ламп. Как известно, исполь­зование обычных ламп в диапазоне сантиметровых и тем более мил­лиметровых длин волн затруднено влиянием инерции электронов и распределенных реактивных проводимостей.

В электронных приборах, специально предназначенных для ис­пользования в диапазоне СВЧ, устранение влияния реактивностей достигается тем, что сам прибор составляет единое целое с коле­бательной системой. В связи с этим при рассмотрении принципа действия и характеристик прибора приходится учитывать и свойст­ва колебательной системы, а также влияние нагрузки, связанной с ней. Конечное время пролета электронов в междуэлектродном пространстве, значительно превышающее период сверхвысокочастот­ных колебаний, в электронных приборах диапазона СВЧ использует­ся для формирования модулированного по плотности электронного потока и взаимодействия сформированного потока с высокочастот­ным полем. Формирование потока по плотности происходит обычно в результате модуляции электронов по скорости.

Виды приборов. Процессы модуляции по скорости, группирования электронов в сгустки (модуляции по плотности) и передачи энергии высокочас­тотному полю могут происходить либо одновременно на всем про­тяжении активной части прибора, либо разновременно на опреде­ленных участках пространства.

Приборы, использующие первый принцип, можно назвать приборами с непрерывным взаимодействием или приборами типа ламп бегущей волны. Второй принцип лежит в основе работы приборов с прерывистым взаимодействием, или при­боров клистронного типа (пролетный и отражательный клистроны).

Следует особо подчеркнуть, что природа основных физических процессов, происходящих в обеих группах приборов, одинакова. Более того, между двумя группами приборов не существует резкой границы, что позволяет все указанные приборы рассматривать на основе общих представлений об отмечавшихся ранее процессах не­зависимо от того, совершаются ли они одновременно или разновременно и на определенных участках междуэлектродного пространст­ва или на всей его длине.

Наиболее отчетливо все эти процессы проявляются в клистро­нах - приборах с прерывистым (дискретным) взаимодействием электронного потока с переменными электрическими полями резонаторов

2. Модель прибора клистронного типа

Модель прибора. Простейшая модель прибора клистронного типа (рис.1) представляет собой последовательно расположенные электронную пушку, модулятор, пространство дрейфа, устройство для отбора энергии от сгруппированного в сгустки электронного потока и коллектор

Электронная пушка предназначена для создания потока электронов, модулятор – для модуляции электронов по скорости, пространство дрейфа электронов – для группирования электронного потока в сгустки и коллектор – для сбора «отработавших» электронов. Такая модель находит воплощение в двухрезонаторном пролетном клистроне

Устройство клистрона. Пролетный клистрон представляет со­бой электронный прибор, предназначенный для усиления или гене­рирования СВЧ колебаний.

Схема устройства двухрезонаторного клистрона показана на рис.2.

В состав клист­рона входят: электронная пушка,

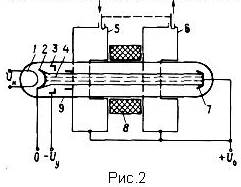
состоящая из ка­тода 2 с подогревателем 1 и управляющего электро­да 3 и создающая поток электронов 4; входной резонатор (модулятор) 5.; выходной резонатор (устройство для отбора энергии) 6; коллектор 7 для сбора «отработавших» электронов, вылетающих из выходного резонатора, и баллон 9 для сохранения высокого вакуума.

Пространство между резонаторами клистрона представляет собой пространство дрейфа. Конструкция резонаторов может быть различной, но наиболее часто используются резонаторы тороидального типа, представляю­щие собой полые цилиндры, длина образующей которых в централь­ной части значительно меньше длины образующей на периферии.То­роидальные резонаторы позволяют получить в центральной части сильное практически однородное электрическое поле, направленное перпендикулярно торцевым стенкам резонатора, т.е. вдоль линии движения электронного потока в приборе. Для того чтобы обеспе­чить прохождение электронного потока, в стенках центральной час­ти резонатора имеются отверстия, которые часто с целью получе­ния большей однородности поля делаются сетчатыми. Пространство между стенками, в котором может осуществляться взаимодействие электронного потока с полем резонатора, обычно называют зазо­ром. Степень взаимодействия потока с полем определяется как

свойствами потока, так и свойствами резонатора. Связь резонато­ров с внешней нагрузкой может осуществляться либо с помощью ок­на связи (в случае волноводной нагрузки), либо с помощью штыря связи, расположенного в пуч-

ности электрического поля, либо с помощью петли связи.

Резонаторы, как правило, соединяются между собой электри­чески, и на них подается высокий положительный потенциал отно­сительно катода - от сотен вольт до сотен киловольт. В простей­шем случае этот же потенциал имеет и коллектор.

Если в состав электронной пушки входит управляющий элект­род, то на него подается отрицательный потенциал относительно катода. Изменение этого потенциала позволяет управлять током луча.

Фокусировка луча в клистроне обычно осуществляется с помо­щью внешнего магнитного поля, создаваемого электромагнитом 8 или постоянным магнитом. В маломощных клистронах непрерывного действия часто используется фокусировка луча только за счет по­ложительных ионов, образующихся в рабочем пространстве прибора.

Принцип действия. Принцип действия пролетного клистрона ос­новывается на физических процессах: модуляции электронов по скорости, группировании их в плотные сгустки и взаимодействии электронов с электромагнитным полем резонатора.

Пусть в пролетном двухрезонаторном клистроне (см. рис.2) в первый резонатор (модулятор) вводятся электромагнитные коле­бания. При этом между сетками резонатора создается высокочас­тотное напряжение, модулирующее электроны в луче по скорости.

Электроны, заторможенные в модуляторе, в пространстве дрей­фа будут иметь скорость, меньшую постоянной скорости потока v₀ , обусловленной постоянным напряжением резонатора U₀ , а ус­коренные электроны - скорость, большую скорости v₀ . Поэтому электроны, вышедшие из модулятора во время действия в нем тормозящего поля, будут двигаться медленнее электронов, не получивших никакого приращения скорости, но вышедших позже.

В последующие моменты времени, когда переменное поле в мо­дуляторе станет ускоряющим, электроны, вышедшие из модулятора позже предыдущих, в пространстве дрейфа будут двигаться уско­ренно по сравнению с электронами, не получившими приращений скорости, т.е. будут догонять эти электроны, сближаясь с ними. С другой стороны, заторможенные электроны, вышедшие раньше, двигаясь медленнее всех других электронов потока, также будут сближаться в относительном движении с электронами, имеющими скорость v₀ . В результате около последних образуются области с повышенной плотностью электронов - электронные сгустки, при­чем они образуются около электронов, во время пребывания кото­рых в модуляторе переменное поле изменялось с тормозящего на ускоряющее. Около электронов, не получивших приращения скорос­ти и находившихся в модуляторе при переходе поля от ускоряюще­го к тормозящему, наоборот, образуются разрежения, т.е. облас­ти с пониженной плотностью электронов. Действительно, в этом случае электроны, вышедшие из модулятора раньше, ускоряются, а вышедшие позже, замедляются, т.е. в пространстве дрейфа ус­коренные электроны уходят от электронов, двигающихся со ско­ростью v₀ , а замедленные отстают от последних.

Таким образом, в пространстве дрейфа электронный поток оказывается модулированным по плотности.

Группирование электронов в сгустки в пространстве дрейфа можно проиллюстрировать с помощью пространственно-временной диаграммы движения электронов (рис.3). На этой диаграмме по оси абсцисс отложено время, а по оси ординат - расстояние, на которое удалился электрон от середины модулятора. Здесь же вдоль оси абсцисс показано переменное напряжение u , действующее в модуляторе и оказывающее неодинаковое влияние на электроны по­тока.

Выделим из всего потока электронов только те электроны, ко­торые соответствуют экстремальным и нулевым значениям напряже­ния модулятора.

Если бы переменное напряжение отсутствовало, то пространст­венно-временные кривые, определяющие положение электронов, про­шедших середину модулятора во время t₁ , t₂ и т.д., пред­ставляли бы собой параллельные прямые линии, наклон которых оп­ределялся бы значением скорости v₀ , так как производная dx/dt характеризует скорость электронов.

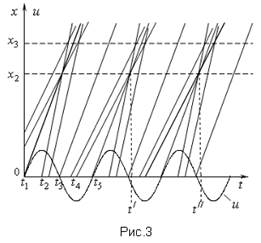
При наличии переменного напряжения на сетках модулятора выделенные электроны получают различные приращения скорости, вследствие чего наклон прямых линий к оси абсцисс для ускорен­ных электронов уменьшится (производная dx/dt увеличится), для замедленных - увеличится (производная dx/dt уменьшится), а для электронов с неизменной скоростью останется прежним. Вследствие этого прямые линии будут пересекаться на некотором расстоянии x₂ от середины модулятора. Точки пересечения со­ответствуют сгусткам электронов, так как они свидетельствуют о наличии в окрестности точки х₂ в моменты времени t^’ , t^’’ и т.д. большого количества электронов. Наоборот, около электрона, вылетевшего в момент времени t₃ , образуется раз­режение. В дальнейшем на расстоянии х₃ > х₂ образуются два фокуса.

Картина получится более наглядной, если помимо выделенных на оси абсцисс электронов рассмотреть еще ряд промежуточных. Это не сделано лишь с целью сохранения ясности рисунка.

Следующие друг за другом сгустки электронов попадают во второй резонатор и наводят в нем высокочастотный ток. Связанное с этим током высокочастотное поле взаимодействует с электронным потоком и отбирает у него энергию. Для эффективного отбора энергии необходимо, чтобы сгустки электронов входили во второй резона

тор во время действия тормозящего полупериода электро­магнитного поля. Это обеспечивается автоматически, так как при­чиной появления поля являются сгустки электронов, отдающие свою энергию полю. Следовательно, сгустки электронов вызывают появ­ление поля с необходимой фазой и взаимодействуют с этим полем, увеличивая его энергию. Увеличенная (усиленная) энергия отво­дится из второго резонатора во внешнюю нагрузку.

Виды пролетных клистронов. Взаимодействие сгустка электро­нов с полем резонатора приводит к уменьшению средней скорости сгустка. С другой стороны, электроны, находящиеся на участке разрежения, попадают в резонатор во время действия ускоряюще­го полупериода поля, а поэтому ускоряются и, выйдя из резона­тора, догоняют сгусток и уплотняют его. Если на пути электрон­ного луча поместить еще один резонатор, то можно добиться еще большего уплотнения сгустка, а значит, и большего усиления мощ­ности за счет лучшего группирования электронного потока. При этом энергия отводится из третьего резонатора. На описанном принципе основана работа многорезонаторных клистронов.

Пролетный клистрон может использоваться не только в усили­тельном режиме, но и в автогенераторном, т.е. для генерирования колебаний. В этом режиме второй (или любой последующий в многорезонаторном 'клистроне) резонатор связывается с первым по внеш­ней цепи, как показано на рис.2 штриховой линией. В любых элементах схемы имеются флюктуационные колебания многих частот. Есть они и в резонаторах, причем наибольшая их амплитуда соот­ветствует резонансной частоте. Первоначально небольшие колеба­ния могут вызвать формирование слабо выраженных сгустков элект­ронов в луче, которые будут способствовать увеличению амплиту­ды поля во втором (или последующих) резонаторе. Если длина внешней линии связи выбрана правильно, то усиленные колебания будут поступать в первый резонатор в такой фазе, что возникаю­щее в резонаторе электрическое поле приведет к модуляции луча по скорости, последующему его группированию в сгустки и прохож­дению сгустков во втором резонаторе в тормозящий полупериод по­ля (условие баланса фаз). А это, в свою очередь, вызовет даль­нейшее увеличение энергии во втором резонаторе. Если энергия, теряемая в резонаторах и во внешних цепях (в том числе и в на­грузке), меньше энергии, поставляемой сгруппированным электрон­ным потоком, то этот процесс будет развиваться до тех пор, по­ка не установится некоторая величина поля в обоих резонаторах, определяемая равенством указанных энергий (условие баланса амп­литуд).

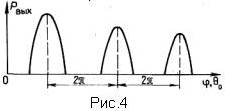
Изменение длины внешней линии связи приводит к срыву авто­колебаний, так как не соблюдается описанное ранее условие не­обходимого соответствия фаз напряжений в первом и. втором резо­наторах. Путем изменения ускоряющего (постоянного) напряжения также можно прекратить автоколебания, так как при этом наруша­ется условие баланса фаз внутри самого прибора за счет времени пролета электронов. Как в том, так и в другом случае появление и срыв автоколебаний (а значит, наличие или отсутствие мощности Р_вых на выходе клистрона) носит периодический характер, т.е. при изменении либо длины внешней линии связи (угла j), ли­бо ускоряющего напряжения (угла пролета θ₀) образуются зоны генерации клистрона (рис.4).

Наряду с усилительны­ми и автогенераторными пролетными клистронами ши­роко используются умножительные клистроны, принцип действия которых мало отличается от рассмотренного ранее. Возможность умноже­ния частоты в клистроне основывается на присутствии в конвекционном токе высших гармонических составляющих со зна­чительными по величине амплитудами. Так, например, амплитуда десятой гармоники всего лишь в два раза меньше амплитуды пер­вой гармоники. Выходной резонатор умножительного клистрона на­страивается на n - ую гармонику возбуждающих колебаний.

Электронные сгустки в умножительном клистроне по-прежнему поступают в выходной резонатор с частотой возбуждающих колеба­ний, т.е. возбуждение выходного резонатора производится один раз за n периодов колебаний в нем. Умножительные клистроны позволяют получить колебания весьма высоких частот (порядка нескольких десятков и даже сотен гигагерц).

3. Анализ основных процессов

Модуляция электронного потока по скорости. Вернемся к модели прибора клистронного типа, изображенной на рис.1. Здесь показаны, в частности, две сетки, на которые может быть подано высокочастотное напряжение, изменяющееся по закону u = U_msinwt.

Потенциал сеток и коллектора относительно катода одинаков и равен U₀ , так что электроны, эмитированные катодом, при отсутствии переменного напряжения на сетках летят в пространстве между сетками и в пространстве за сетками с постоянной скоростью v₀= (2eU₀/m)^1/2.

Предположим вначале, что время пролета электронов между сетками намного меньше периода высокочастотного напряжения, тогда можно считать, что движение каждого электрона между сетками происходит при постоянном (мгновенном) значении переменно­го напряжении.

Скорость электронов, вышедших из модулятора, определяется выражением

v = v₀+Dv =( 2e/m) (U₀+U_msinwt).(1)

Закон модуляции скорости электронов в общем случае отлича­ется от синусоидального, как это видно из выражения (1).Од­нако если амплитуда U_m мала по сравнению с постоянным напря­жением U₀ (малые сигналы), то выражение (1) может быть с достаточной степенью точности представлено первыми двумя чле­нами разложения в ряд, т.е.

v=v₀ (1+ 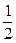x sinwt), (2)

где x=U_m/U₀ ; v₀ = (2eU₀/m)^1/2.

Тогда можно считать скорость электронов, вылетающих из мо­дулятора, модулированной по синусоидальному закону.

Если время пролета электронов соизмеримо с периодом высо­кочастотного напряжения, то амплитуда изменения скорости элект­ронов уменьшается по сравнению с амплитудой, определяемой выра­жением (2). Снижение амплитуды скорости можно учесть путем усреднения напряжения, действующего на электрон за время про­лета в модуляторе. Для облегчения этой операции примем во вни­мание, что x<<1 , а поэтому время нахождения в модуляторе любого электрона практически неизменно и равно среднему време­ни пролета

τ₁=d₁ /v₁ , (3)

где d₁. - расстояние между сетками модулятора.

Кроме того, будем отсчитывать время t₁ от момента нахожде­ния электронов в середине модулятора. Тогда время влета элект­ронов в модулятор будет равно t₁ - τ₁/2а время вылета из не­го равно t₁+τ₁/2

Среднее значение высокочастотного напряжения, действующего на электроны за время пролета их в модуляторе, определяется интегралом

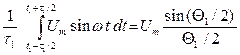
(4) (15.4)

где θ₁=wτ₁- средний угол пролета электронов в пространстве модулятора.

Таким образом, в формуле (1) теперь следует учесть из­менение амплитуды из-за конечного времени пролета электронов в соответствии с выражением (4). Уменьшение амплитуды учитыва­ется коэффициентом

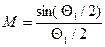(5)

называемым коэффициентом эффективности модуляции, коэффициен­том электронного взаимодействия или коэффициентом связи элект­ронного потока с полем модулятора.

Результирующее выражение для скорости электронов после мо­дулятора с учетом конечного времени пролета электронов в моду­ляторе будет иметь вид

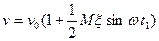(6)

Группирование электронов в пространстве дрейфа. Электронный поток, модулированный по скорости в модуляторе, при дальнейшем движении в пространстве дрейфа становится неоднородным по плот­ности. Иными словами, конвекционный ток зависит как от коорди­наты х, так и от времени t . Для выяснения этой зависимости используем закон сохранения заряда. Выделим в электронном потоке два тонких слоя, вылетаю­щих из модулятора в моменты времени, различающиеся на величи­ну dt₁ . В пространстве дрейфа эти слои сближаются (или расхо­дятся) и на некотором расстоянии ходин слой отстает от друго­го уже на меньшее (или большее) время dt .Из закона сохране­ния заряда следует

i (x,t) dt = I₀ dt₁. (7)

где i (x,t) - конвекционный ток в плоскости х ; I₀ - конвекци­онный ток в плоскости х = 0, т.е. в модуляторе. При этом пред­полагается, что конвекционный ток в середине модулятора такой же, как и до модулятора, т.е. постоянный.

Из выражения (7) можно определить конвекционный ток в пространстве дрейфа:

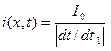(8)

Абсолютная величина производной в выражении (8) принята по той причине, что направление конвекционного тока в прост­ранстве дрейфа не зависит от знака производной. Иными словами, опережение первого слоя вторым не говорит об изменении направ­ления тока, так как электроны движутся в одном и том же направ­лении и в сгустке лишь перераспределяются заряды одного и того же знака.

Выражение для конвекционного тока (8) неудобно для ана­лиза, так как производная текущего времени по времени вылета задана в общем виде. Поэтому предварительно следует определить указанную производную.

Время t прихода в точку х электрона, прошедшего середи­ну модулятора (х =0) во время t , можно найти, если извест­на скорость электрона v и приращение скорости, полученное электроном в модуляторе:

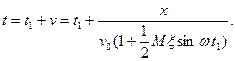(9)

С учетом принятого ранее допущения о малости ξ равенство (9) можно приближенно записать в виде

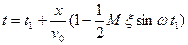(10)

Отсюда непосредственно можно получить интересующую нас произ­водную

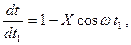(11)

где

(12)

Величина X носит название параметра группирования, а θ₀ –“невозмущенного” угла пролета в пространстве дрейфа, т.е. угла пролета электрона с неизменной скоростью.

Таким образом, выражение (8) теперь можно записать в яв­ной форме:

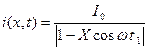. (13)

Полученное выражение говорит о том, что изменение тока как в пространстве, так и во времени имеет явно несинусоидальный характер. Правда, при Х<<1 можно считать приближенно, что конвекционный ток изменяется во времени по синусоидальному за­кону относительно постоянной составляющей I₀ , однако такие режимы практически не используются из-за малой плотности кон­векционного тока.

Зависимость i(t) на различном расстоянии от модулятора (при различных значениях X ) показана на рис. 5.

При построе­нии этой зависимости использовано соотношение (10) с учетом того, что второй член в скобках значительно меньше первого, а поэтому можно принять t = t₁+ θ₀ /ω .

Рассмотрение зависимости конвекционного тока от расстояния и времени позволяет представить общую картину группирования сгустков в пространстве дрейфа.

По вылете из модулятора электроны группируются в сгустки с малой плотностью, и изменение конвекционного тока в пространст­ве и во времени имеет синусоидальный характер. При дальнейшем движении сгустки уплотняются и форма их постепенно трансформируется, так что конвекционный ток и во времени и в пространст­ве изменяется по явно выраженному несинусоидальному закону.

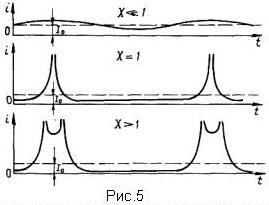
На расстоянии x , соответствующем параметру X =1, сгуст­ки приобретают наибольшую плотность и конвекционный ток стано­вится бесконечно большим (практически из-за действия растал­кивающих сил пространственного заряда пик тока конечен).

При дальнейшем движении в пространстве дрейфа сгустки "раз­дваиваются", т.е. в каждом сгустке образуется два пика, причем эти пики в дальнейшем расходятся, двигаясь в направлении оси х с разными скоростями. Физически образование двух пиков конвек­ционного тока объясняется обгоном электронами, вышедшими позже из модулятора при действии ускоряющего поля, электронов, вышед­ших раньше из модулятора при тормозящем поле. Обгоняющие элект­роны вместе с электронами, заторможенными в модуляторе, но вы­шедшими более чем на полпериода раньше, и образуют новый пик тока.

Спектр конвекционного тока. Рассмотрение зависимости кон­векционного тока от времени показывает, что этот ток богат спектральными составляющими высших порядков особенно при зна­чениях параметра X , близких к единице и больших единицы. Для выяснения спектра конвекционного тока функцию, определяемую вы­ражением (13), нужно разложить в тригонометрический ряд по аргументу ωt . Однако более удобным оказывается разложение ее в ряд по аргументу ωt - θ₀ , так как при этом отпадает необ­ходимость в проведении нескольких промежуточных преобразований.

Разложение функции i(x,t) в тригонометрический ряд позволяет получить

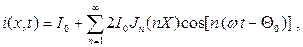(14)

где J_n(nX)—функция Бесселя первого рода n-го порядка.

Таким образом, конвекционный ток в пространстве дрейфа сос­тоит из постоянной составляющей тока I₀ и суммы гармонических составляющих, амплитуда, частота и фаза которых определяются выражением (14).

Амплитуда любой гармоники определяется зависимостью соот­ветствующей бесселевой функции от параметра пХ

Для бесселевых функций первого рода зависимость эта тако­ва, что при увеличе- нии параметра пХ функция вначале, возраста­ет, затем достигает максимума, уменьшается и при больших зна­чениях пХ осциллирует вдоль

оси пХ.На рис.6 изобра­жены кривые,выражающие зависимость относитель­ных амплитуд гармоник от параметра X .

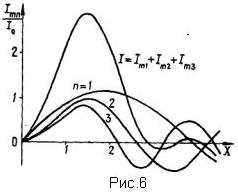
Рассмотрение рисунка показывает, что наиболь­шей амплитудой обладает первая гармоника конвекционного тока при значении параметра X = 1,84.Максимальные значения гармоник более высокого порядка получаются при меньших значениях X , приближающихся к единице. Физически это можно объяснить с помощью рис.6. Бо­лее короткий импульс конвекционного тока с крутыми фронтами, естественно, более богат гармоническими составляющими высших порядков, чем импульс широкий с "расходящимися" пиками.

Амплитуда первой гармоники тока при Х= 1,84 составляет 1,16 I₀ , так как значение бесселевой функции первого рода первого порядка J(I,84) = 0,58. Значение параметра X = 1,84 можно считать оптимальным, так как при этом значении наблюда­ется максимум амплитуды первой гармоники, а следовательно, и оптимальное группирование электронного потока. Это означает, что если, например, уменьшить амплитуду напряжения на сетках модулятора U_m , то в данную точку пространства поток будет приходить "недогруппированным" и амплитуда конвекционного то­ка будет меньше максимальной. При увеличении напряжения U_m амплитуда тока снова уменьшится, но уже из-за того, что поток будет "перегруппирован". Те же результаты для данной точки пространства можно получить изменением любой другой величины, определяющей значение параметра группирования X в соответ­ствии с выражениями (12).

Рассмотрим механизм взаимодействия переменного по плотности электронного потока с возбужденным этим же потоком полем резонатора. Вначале рассмотрим механизм возбуждения коле­баний в резонаторе. Сгруппиро

ванный электронный поток, проходя через зазор резонатора, вызывает в последнем наведенный ток, а на зазоре резонатора - напряжение, тормозящее движение элект­ронных сгустков. В результате этого торможения электронный по­ток отдает резонатору часть энергии, идущую на компенсацию по­терь в резонаторе, т.е. на поддержание в нем колебаний. Предпо­лагается, что конвекционный ток содержит гармонику с частотой, равной собственной частоте резонатора. Такой гармоникой может быть любая, в том числе и первая, которую и будем использовать в дальнейшем для определенности рассуждений. Составляющие кон­векционного тока с частотами, отличающимися от собственной час­тоты резонатора, не будут вызывать заметного напряжения на ре­зонаторе, поэтому их можно не рассматривать.

Первая гармоника наведенного тока во внешней цепи i_н1 связана с первой гармоникой конвекционного тока i_к1 соотношением

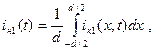
(15)

где d—ширина зазора резонатора, а ток i_к1 определяется формулой

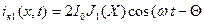) (16)

в которой 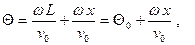(17)

где L—расстояние от середины модулятора (зазора первого резонатора) до середины зазора рассматриваемого резонатора.

Для выполнения интегрирования необходимо уяснить значение функции J₁(X), входящей в выражение (16). Учитывая то об­стоятельство, что угол пролета в зазоре мало изменяется отно­сительно своего среднего значения, а значит, мало изменяется и параметр X , будем считать функцию J₁ (X) постоянной и соот­ветствующей значению X для середины зазора резонатора. Тогда, подставив выражения (16) и (17) в (15) и учтя уменьшение катодного тока в рассматриваемом резонаторе в k раз (из-за “перехвата” резонаторами электронов потока), получим

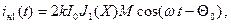
где

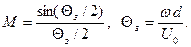
Коэффициент М ранее уже встречался. Он представляет собой коэффициент связи электронного потока с полем резонатора. Фи­зический смысл его в данном случае состоит в том, что он пока­зывает, насколько уменьшается амплитуда наведенного тока по сравнению с амплитудой конвекционного тока. Кроме того, коэф­фициент М указывает на наличие модуляции уже сгруппированного потока по скорости в зазоре рассматриваемого резонатора.

Наведенный ток вызывает появление переменного напряжения на зазоре резонатора с амплитудой

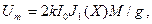
где g - полная активная проводимость резонатора.