Модели деформирования оболочек

ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ И СОПРОТИВЛЕНИЕ ОБОЛОЧЕК

Модели деформирования оболочек

При проектировании зданий и сооружений с несущими конструкциями из оболочек, при конструировании технологического оборудования с включением оболочек крайне важно знать их реальную несущую способность, запас прочности оболочек. Этим обеспечивается гарантия надёжности и безопасности оболочек.

Вопросам определения несущей способности конструкций посвящён один из разделов строительной механики – теория предельного равновесия. Решение задач динамики конструкций с учётом пластических и вязких свойств материалов рассматривается в другом разделе - теории предельного сопротивления [8].

Следует напомнить ряд основных понятий теории пластичности. В частности, на­пряженно-деформированное состояние стержня при растяжении, характеризуется диаграммой напряжений-деформаций 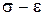. Действитель­ные кривые, иллюстрирующие связи 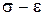, которые получены в экспериментах над стержнями в за­висимости от вида материала (мягкие малоуглеродистые стали и алюминиевые сплавы, железобетон, полимеры и др.), как правило, имеют сложный вид (рис. 13.1,а). Напряжение 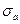, соответствующее точке a графика, приведенного на рис. 13.1,а, называется пределом пропорциональности. Предел пропорциональности – максимальное напряжение, при котором справедлив закон Гука. Обычно этот предел и принимают за предел упругости.

Пределом текучести 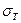называется напряжение, при достижении которого появляется площадка текучести bc.

Ис­пользование в исследованиях действитель­ных кривых, а также в приложениях к расчету кон­струкций, встречает порой непреодолимые трудности. Поэтому на прак­тике эти диаграммы аппроксимируют, огрубляют, выделяя ха­рак­терные участки и принимая их в виде прямых. Таким образом, получают основные моде­ли деформирования одно­мер­ных и многомерных пла­стических систем, таких как: модель жестко­плас­­тической а) и жесткоупрочняющейся б) системы (рис. 13.2,а, б). Если при­нимают во внимание также упругие деформации, возникающие в стержне на начальной стадии нагружения, то приходят ещё к двум мо­делям упругопластических систем: а) упругопластического и б) уп­ругоупрочняющегося деформирования (рис. 13.3,а, б). Пунктиром на схе­­мах показаны участки диаграммы, соответствующие разгрузке стерж­ня. Эти диаграммы достаточно полно характеризуют плас­тические деформации при статическом нагружении. Пластичность - свойство твердых тел приобретать остаточные деформации.

а б

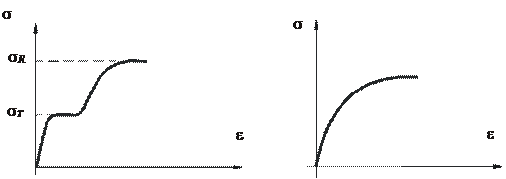Рис. 13.1

а б

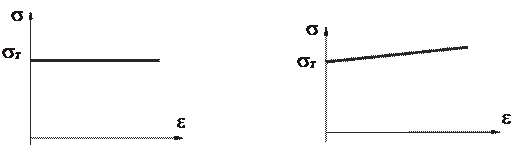Рис. 13.2

а б

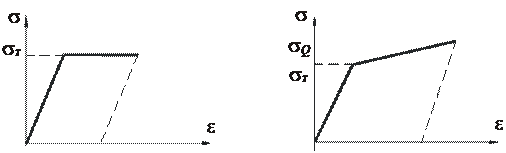Рис. 13.3

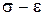От изучения поведения материалов в терминах при рас­смо­трении стержней и систем из них нетрудно перейти к определению обобщенных усилий и соответствующих им деформаций. Например, диаграмме Прандтля (рис. 13.3, а) в переменных соответствует по­добная схема в терминах М и i для изгибаемых элементов (М – из­­­­гибающие моменты, i– кривизна стержня) [12]. Ус­ловием текучести в этом слу­чае служит равенство

М = М_T, (13.1)

где М_T – пластический момент.

При действии динамических нагрузок большое влияние на по­веде­ние пластических систем оказывают эффекты вязкости. Вязкость может проявлять себякак в упругой, так и в пластической стадии де­формирования или только в пластической. В первом случае механические системы называют вязкоупруго­плас­тическими, во втором – вязкопластическими. Наибольшее рас­про­стра­нение в динамике конструкций получила схема жестко­вязко­плас­тического тела, когда упругими деформациями пренебрегают вов­се. Широко используется также модель, где зависимость напря­жений от скорости деформаций при динамическом нагружении при­ни­мается в виде

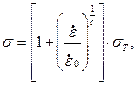(13.2)

где 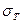- предел текучести при статическом растяжении (рис. 13.4); 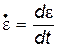- скорость деформаций; c, 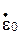- константы материала [8].

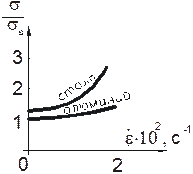Рис. 13.5

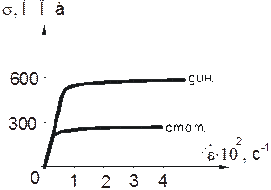Рис. 13.4

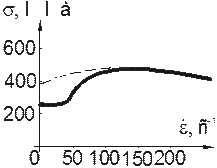Рис. 13.6

Как известно, динамические и ста­тические характеристики ме­тал­­лов раз­­личны – для мягких сталей они пред­­ставлены на рис. 13.4. При дина­ми­ческом нагружении проис­хо­дит уве­­личение предела теку­чес­ти ма­те­риала. В экспериментах об­наружено, что металлы, имеющие хоро­шо вы­ра­женный предел те­кучести, особенно чувствительны к скорости дефор­ма­ции. Например, для мягких сталей установлено, что вместе с ростом скорости деформации предел текучести рас­тет от значения 276 МПа (статический предел те­ку­чести) до 587 МПа при скорости дефор­мации 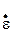» 200 с^-1. Предел текучести рас­тет до того момента, пока не достигнет кривой условного пре­дела проч­ности (пунк­­тирная линия на рис. 13.6). Ус­ловный предел проч­­­ности воз­рас­тает в области скоростей де­формаций от 0 до 200 с^-1.