НАПРЯЖЁННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ПЛАСТИН

Пластиной (плитой)называется тело призматической или цилиндрической формы, высота (толщина) которого намного меньше других размеров (рис. 1.1).

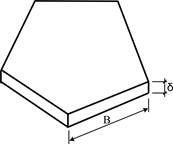
Рис. 1.1

Плоскость, параллельная основанию пластинки и разделяющая её высоту пополам, называется срединной плоскостью. Линия пересечения срединной плоскости с боковой поверхностью пластины называется контуром.

В пособии рассматривается теория расчёта тонких пластин, для которых отношение толщины 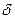к наименьшему другому размеру пластины находится в пределах

.

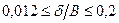Возможные прогибы пластины также малы по сравнению с толщиной; верхний предел величины прогиба составляет 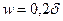. Если соотношения в размерах плиты не отвечают указанным условиям, то она относится к разряду плит средней толщины или толстых плит.

1. 1. Основные предпосылки теории расчёта тонких пластин

Техническая теория расчёта пластин основана на двух допущениях, упрощающих исследование:

I. Статическая гипотеза – нормальные напряжения, возникающие при деформировании вследствие взаимного нажатия горизонтальных слоёв пластинки друг на друга, на площадках, параллельных срединной плоскости, считаются нулевыми .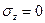

Это означает, что бесконечно тонкий слой находится в условиях плоского напряжённого состояния. К тому же и касательные напряжения 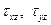относятся к второстепенным. Они также принимаются равными нулю.

II. Кинематическая гипотеза – прямая, перпендикулярная срединной поверхности в начальном положении, остаётся перпендикулярной к поверхности и в деформированном состоянии (гипотеза прямых нормалей Кирхгофа) (рис. 1.2).

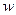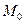На рис. 1.2 показаны прогиб точки срединной плоскости в сечении, параллельном оси Ох, и перемещение 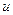произвольной точки 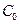, отстоящей на расстоянии 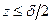; угол наклона нормали, обусловленный изгибом пластинки, обозначен через .

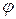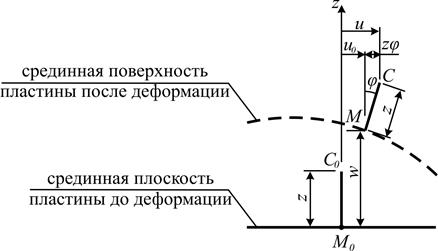
Рис. 1.2

Данная гипотеза, по существу, вытекает из первого предположения. Действительно, из условия отсутствия касательных напряжений 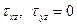следует, что деформации сдвига 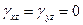. Как известно, в технической теории изгиба балок принята аналогичная гипотеза плоских сечений [5].

Поскольку нормальные напряжения 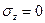, то деформации срединной плоскости согласно физическим соотношениям теории упругости находят по формулам [3]:

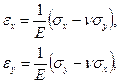(1.1)

,

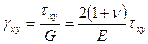где 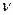- коэффициент Пуассона (для стали 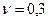), 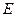- модуль упругости материала (для стали 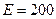ГПа),

Отсюда нетрудно установить обратную зависимость напряжений от деформаций:

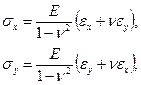(1.2)

.

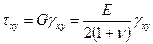На основании первой гипотезы

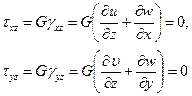
можно утверждать, что

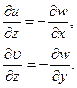
Интегрируя последние соотношения с учётом граничных условий на срединной поверхности пластинк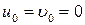и ( при 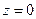), легко установить характер изменения перемещений точки 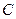, взятой на некотором удалении 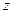от срединной плоскости, а именно:

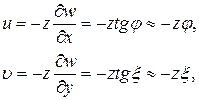(1.3)

где 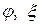- углы наклона нормали с осями координат[*].

1.2. Распределение напряжений и моментов при изгибе пластин

Деформации (1.1) элемента срединной плоскости пластинки в направлении осей координат (рис. 1.3) с учётом (1.3) можно найти по формулам:

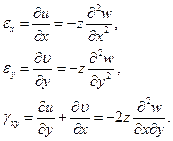(1.4)

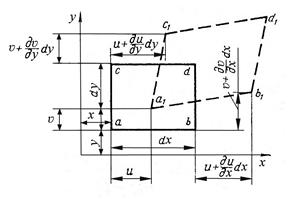
Рис. 1.3

Приравнивая правые части выражений (1.1) и (1.4), в результате решения полученной системы нетрудно установить распределение нормальных и касательных напряжений по высоте пластинки (рис. 1.4):

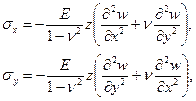(1.5)

.

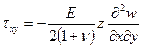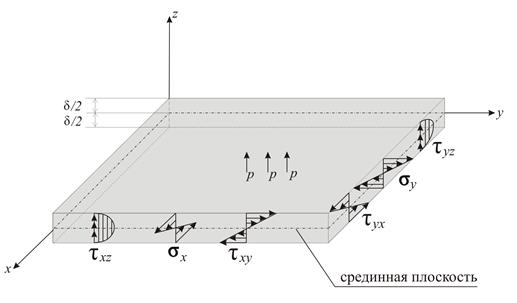
Рис. 1.4

Величины изгибающих моментов и поперечных сил, действующих на боковых гранях элемента пластинки, определяют путём интегрирования функций напряжений по толщине пластинки, т. е.

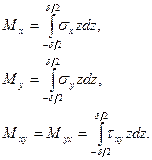
Подставив сюда выражения для напряжений (1.5), легко найти:

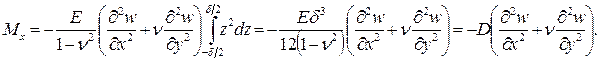(1.6,а)

Аналогично находят и величины:

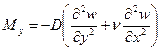, (1.6,б)

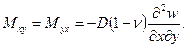(1.6,в)

Здесь 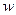- прогиб произвольной точки; 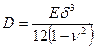- цилиндрическая жёсткость пластинки, - её толщина, 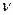- коэффициент Пуассона (рис. 1.5).

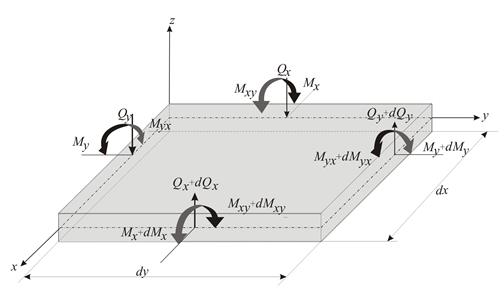
Рис. 1.5

1.3. Вывод дифференциального уравнения изгиба пластинки

При рассмотрении равновесия элемента тонкой пластинки, подверженной действию внешней распределённой нагрузки 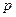, нормальной к срединной плоскости, кроме изгибающих моментов следует учитывать также поперечные силы

.

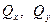Несмотря на то, что в соответствии с первой предпосылкой теории расчёта пластинок деформации 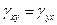пренебрежимо малы, поперечные силы 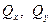имеют тот же порядок малости, что и величина нагрузки 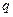. Иначе, как тогда объяснить возможность сохранения условия равновесия элемента в направлении оси Оz в виде :

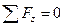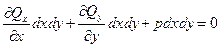
или

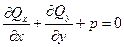. (1.7)

Условие равновесия элемента 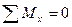после отбрасывания слагаемых высшего порядка имеет вид

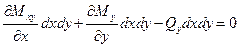
или

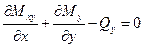. (1.8,а)

Аналогично, из условия 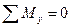следует, что

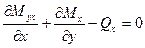. (1.8,б)

В результате исключения поперечных сил из приведенных условий равновесия приходят к одному условию

.

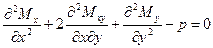Подставив сюда величины моментов согласно (1.6), условие равновесия пластинки можно выразить через прогибы

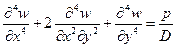. (1.9,а)

Это условие называется уравнением изогнутой поверхности тонкой пластинки. С использованием оператора Лапласа

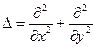
оно записывается намного короче в виде

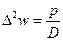. (1.9,а)

Здесь 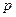- интенсивность поверхностной нагрузки.

Дифференциальное уравнение изгиба пластинки (1.9) установлено Лагранжем в связи с обсуждением статьи Софи - Жермен в 1811 г. [16].

Величины поперечных сил несложно выразить через прогибы пластинки, воспользовавшись их определением из формул (1.8) с привлечением (1.6):

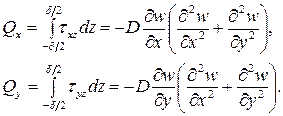(1.10)

1.4 Процедура анализа НДС пластин.

Аналогии с решением плоской задачи теории упругости

Процесс анализа НДС пластин заключается в интегрировании дифференциального уравнения изгиба (1.9) с учётом граничных условий, т. е. условий опирания на контуре пластины. Действительно, если будет найдено решение уравнения, т. е. поле прогибов срединной плоскости 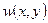, то с помощью формул (1.6) и (1.10) можно без труда найти значения изгибающих моментов и поперечных сил в любой точке пластинки.

Очевидно, уравнение изогнутой поверхности пластинки при нулевой правой части, как и бигармоническое уравнение функции напряжений в плоской задаче теории упругости, является разрешающим уравнением при анализе изгиба пластинок [5]. Следовательно, функция напряжений характеризует изогнутую поверхность пластинки при её нагружении моментами или (и) поперечными силами, прикладываемыми на контуре.

Ещё одна аналогия наблюдается и в самих граничных условиях, а именно: статическим граничным условиям плоской задачи теории упругости соответствуют кинематические граничные условия фиктивного поперечного изгиба пластинки, и наоборот.

1.5 Формулировка граничных условий пластинки

Граничные условия пластинки можно формулировать в терминах перемещений или усилий.

Описание граничных условий можно начать с составления условий для прямоугольной пластинки с различным характером опирания кромок:

а) жёстким защемлением, б) шарнирным прикреплением и в) свободным краем (рис. 1.6).

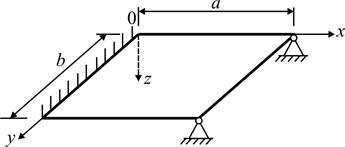
Рис. 1.6

а) Обращаясь к жёсткой кромке, легко установить, что вдоль неё (при 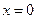) прогибы как и уголы наклона касательной к срединной плоскости по отношению к оси Ох равны нулю, т.е.

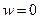и 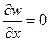. (1.11,а)

б) Для шарнирной кромки характерно отсутствие прогиба и нормальных напряжений по опорному сечению и касательных напряжений 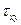, имеющих направление, параллельное оси Ох. Касательные напряжения, параллельные оси 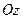, уравновешивают опорные реакции. В аналитической форме граничные условия

при ,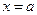

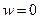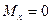
на основе определения 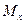по (1.6,а) можно представить только через перемещения:

при 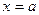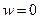, , 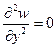, 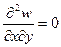(1.11,б)

т. к. вторая производная по этой же кромке заведомо нулевая, т. е. 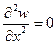. Аналогично,

при 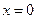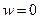, , 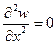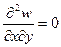. (1.11,в)

Данные условия можно несколько смягчить, отказавшись от последнего из них и принять граничное условие в интегральной форме, получив его путём суммирования касательных напряжений по толщине пластинки и приведения их к системе взаимно уравновешенных усилий на кромке (см. подраздел1.6).

в) На свободном крае напряжения 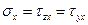и соответствующие им усилия 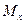, , 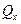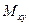равны нулю. На основе формул (1.6), (1.10) можно составить три условия:

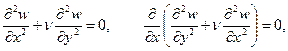
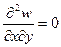. (1.12)

Однако для интегрирования уравнения (1.9) достаточно иметь всего по два условия на каждой кромке. Оставив без изменения первое, два других можно свести к одному путём объединения касательных напряжений 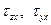, точнее, путём сложения соответствующих им поперечной силы 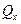и силы F 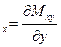, отвечающей крутящему моменту 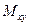(рис. 1.7):

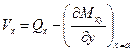. (1.13)

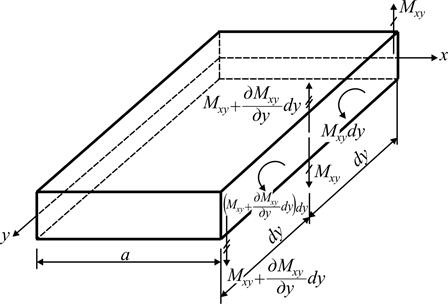
Рис. 1.7

Действительно, действие крутящего момента 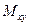на элементарном отрезке длиной 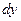эквивалентно паре сил с модулем, равным 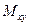. На соседнем участке момент получает приращение и становится равным

.

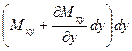Ему соответствует пара сил

.

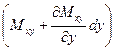Складывая полученные силы в пределах каждого элементарного отрезка, можно утверждать, что на единицу длины кромки в направлении оси у действует сила 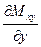. В итоге по всей длине кромки в каждой её точке, кроме поперечной силы 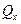, следует принимать во внимание действие дополнительной силы 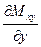, направление которой противоположно 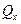. В совокупности они составляют так называемую приведенную поперечную силу 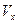. После дифференцирования момента (1.6,в) с учётом определения 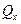по (1.10) выражение приведенной поперечной силы 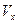на кромке 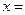const принимает вид

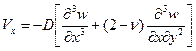. (1.14,а)

Аналогично, по краю 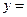const

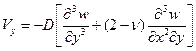. (1.14,б)

Очевидно, на свободной кромке момент и приведенная сила отсутствуют; следовательно,

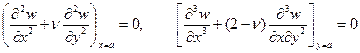. (1.15)

При шарнирном опирании на кромке приведенная сила уравновешивается реакциями опоры. А поскольку в составе приведенной силы имеется часть, соответствующая крутящему моменту на кромке, то это приводит к появлению в углах пластинки дополнительных ответных сосредоточенных сил реакций 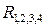,причем

.

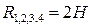Таким образом, приведенные поперечные силы 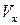и 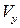представляют собой распределенные опорные реакции пластины, а силы 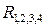- сосредоточенные реакции в угловых точках (рис. 1.8).

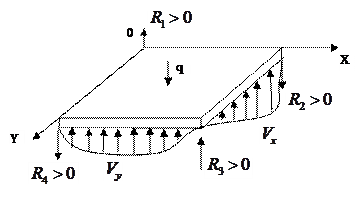
Рис. 1.8

Граничные условия для круглых или эллиптических пластинок рассматриваются в разделе 2 п . 2.2.

1.6 Принцип возможных перемещений

Потенциальная энергия изогнутой пластинки, отнесённая к единице объёма

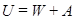, (1.16)

складывается из энергии упругих деформаций

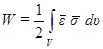(1.17,а)

и потенциала поверхностной нагрузки р

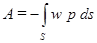. (1.18)

Здесь 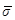- вектор напряжений, распределённых в объёме 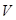пластинки; 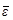- вектор деформаций, в общем случае связанный с перемещениями 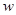дифференциальными соотношениями (1.4); 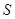– площадь поверхности, на которой распределена нагрузка р.

Принимая во внимание компоненты вектора напряжений согласно (1.5),

нетрудно подсчитать энергию упругих деформаций, отнесённую к единице объёма:

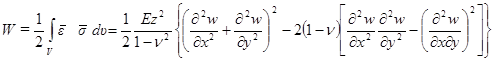. (1.17,б)

Потенциальная энергия всей пластинки находится путём интегрирования выражения (1.17,б) по всему объёму пластинки с учётом того, что переменная 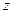меняется в пределах от 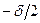до 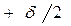, а также суммирования внешнего воздействия по поверхности т. е. .

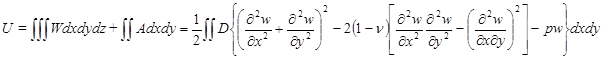(1.18)

Потенциальную энергию пластинки можно выразить и через усилия 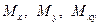, воспользовавшись их определением по (1.6).

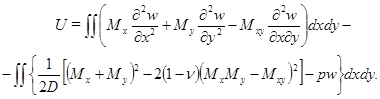(1.19

В соответствии с вариационным принципом Лагранжа в состоянии равновесия элемента пластинки величина потенциальной энергии принимает стационарное значение, причём в положении устойчивого равновесия этот экстремум является минимумом.

Условие минимума функционала энергии

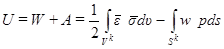
имеет вид

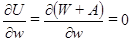. (1.20)

Следовательно, из всех кинематически возможных перемещений 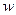элемента состоянию равновесия отвечают те, которые сообщают минимум величине полной потенциальной энергии .

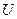Кинематически возможные перемещения, непрерывно изменяющиеся по полю пластинки, можно задать в виде некоторого приближения к истинному или действительному распределению перемещений. При этом возможные перемещения должны удовлетворять граничным условиям.

Выражение энергии (1.19) используется в лекции № 3 для обоснования связи вариационного принципа Лагранжа и метода Бубнова - Галёркина. В лекции № 4 вариационный принцип Лагранжа служит основанием для вывода разрешающего уравнения метода конечных элементов.

1.7 Методы интегрирования уравнения изгиба

прямоугольных пластин

Как правило, интегрирование уравнения изгиба пластин, осуществляется обратным способом. В таком случае задаются ожидаемым распределением прогибов срединной плоскости.

Например, для прямоугольной пластинки, шарнирно опёртой по всему контуру, в качестве возможного распределения прогибов Навье (1820) было предложено воспользоваться двойным тригонометрическим рядом [16]

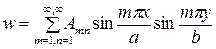, (1.21)

который автоматически удовлетворяет указанным краевым условиям

,

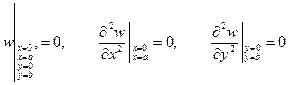а неизвестные коэффициенты ряда 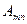искать на основе решения уравнения (1.10).

Подставив выражение прогиба (1.21) в уравнение, после небольших преобразований можно установить, что

.

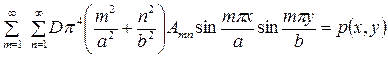Умножив полученное равенство на 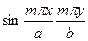и проинтегрировав его по х от нуля до а и по у от нуля до b, приходят к соотношению

,

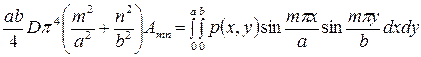из которого легко установить коэффициенты

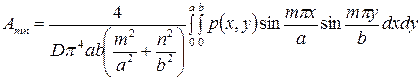. (1.22)

При интегрировании левой части были использованы известные интегралы произведений тригонометрических функций

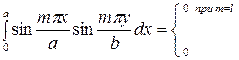
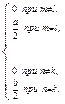
Зная коэффициенты 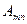, можно вычислить прогибы согласно (1.21). Например, при действии равномерной нагрузки постоянной интенсивности р, нетрудно определить величину интеграла

,

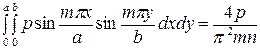где 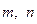- нечётные числа. Благодаря этому становится известным поле прогибов пластинки

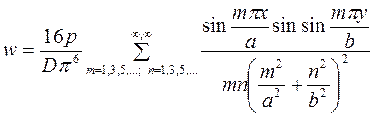. (1.23)

Максимальный прогиб пластинки имеет место в центре

.

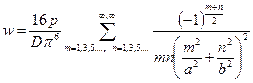Значения изгибающих моментов и поперечных сил в сечениях пластинки определяют по формулам (1.6)- (1.7). Полученное решение можно использовать для анализа состояния пластинки при действии сосредоточенной силы, приложенной в точке .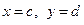

Ещё один аналитический метод интегрирования уравнения изгиба пластинок разработал М. Леви (1899) [6]. В качестве допустимого поля прогибов он принял выражение прогиба на основе одинарного тригонометрического ряда

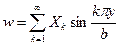, (1.24)

где 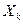- неизвестные коэффициенты ряда, являющиеся функциями только координаты х. Для ихопределения следует найти производные выражения (1.24) и подставить в уравнение (1.10). В результате приходят к равенству

.

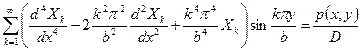Умножив обе части равенства на 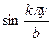и выполнив интегрирование по у в пределах от 0 до b, выводят уравнение

.

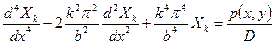Общее решение данного дифференциального уравнения

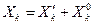(1.25)

складывается из частного решения 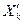, соответствующего правой части, и решения однородного дифференциального уравнения

.

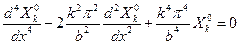Решение последнего уравнения находят с помощью подстановки

,

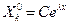где С - постоянная интегрирования. Соответствующее характеристическое уравнение имеет вид

.

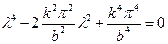Корни этого уравнения

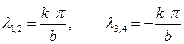
указывают на существование решения однородного уравнения в виде

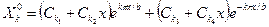. (1.26)

Частное решение

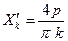
при действии равномерной нагрузки постоянной интенсивности р определяется по аналогии с решением Навье. При вычислении прогибов пластинки следует принимать во внимание также характер опирания кромок. Например, при шарнирном опирании контура постоянные интегрирования в (1.26) должны быть установлены из краевых условий на сторонах :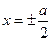

,

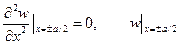или

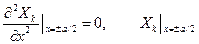
С учётом их соблюдения в результате несложных преобразований можно получить функцию

,

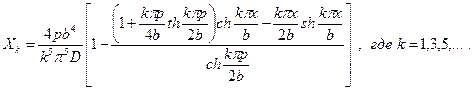которая служит коэффициентами ряда (1.24).

Данный ряд обладает удивительной сходимостью, свидетельством чего служит следующий факт. Если ограничиться только одним членом ряда (k=1), то прогиб в центре определяется по формуле

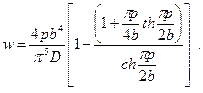(1.27)

Для квадратной пластинки согласно этой формуле

,

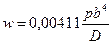что лишь на 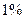отличается от точного значения.

Изгибающие и крутящие моменты определяют на основе формул (1.6) и (1.25):

.

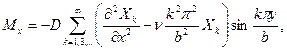
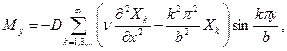
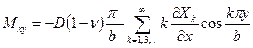[*] На рис. 1.2 показан случай, соответствующий граничному условию .