Основные типы задач на растяжение- сжатие

При растяжении сжатии в поперечных сечениях возникает только нормальное напряжение:

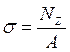
где, А – площадь поперечного сечения.

Условие прочности при растяжении (сжатии):

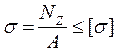
Пользуясь этим условием, можно решать следующие задачи:

1. Проверять прочность стержня 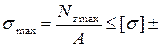5%;

2. Определять размеры поперечного сечения стержня (основная задача СМ):

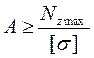
3. Определять величину допускаемой продольной силы:

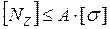
Расчеты на прочность.

В некоторых случаях работоспособность конструкции определяется величиной предельной деформации [Δl]:

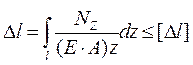
где: Е – модуль продольной упругости.

Это неравенство называют условием жесткости, а расчеты – расчетами на жесткость.

Сдвиг

Сдвигомназывается такое напряженное состояние, при котором в поперечном сечении возникает только один ВСФ – поперечная силаF_y (Q_y).

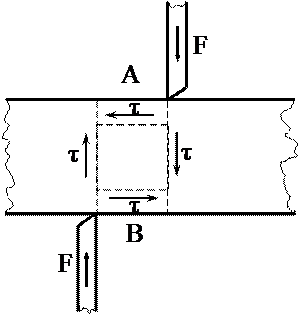
Если нагрузить брус, как показано на рисунке, то при определенной величине сил F произойдет срез – разделение бруса на 2 части по сечению АВ.

Касательные напряжения при срезе определяются соотношением:

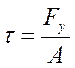
где А – площадь поперечного сечения.

Условие прочности при срезе:

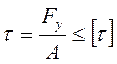
где [t] - допускаемое напряжение при срезе принимается:

[t] = (0,5÷0,6)·[σ]_Р - для пластичных материалов;

[t] = (0,7÷0,9)·[σ]_Р - для хрупких материалов.

На срез рассчитываются заклепочные, сварные, шпоночные и шлицевые соединения.

Кручение

Стержень, работающий на кручение называется валом.

Кручением называется такое напряженное состояние, при котором в поперечном сечении возникает только один ВСФ – крутящий момент M_Z (Т_К). Его величину определяют методом сечений. Крутящий момент является моментом внутренних сил упругости и численно равен моменту внешних сил, действующих по одну сторону сечения.

Правило знаков для крутящих моментов представлено на плакате.

Наглядное представление о величине M_Z в любом сечении вала дают эпюры крутящих моментов.

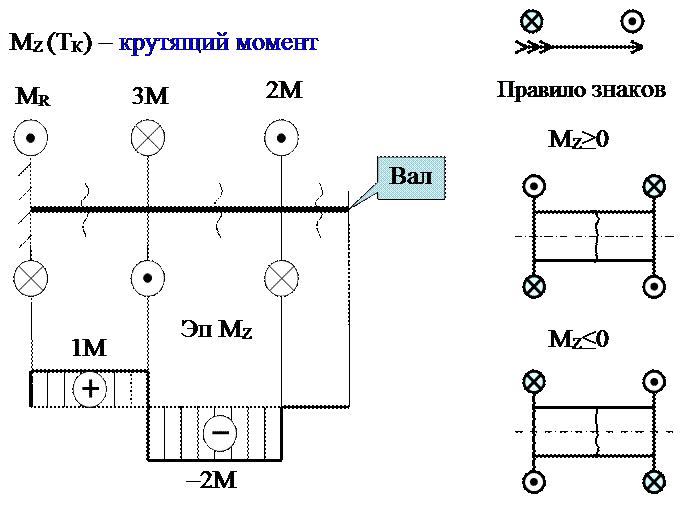
Определим крутящие моменты в нашем примере методом сечений от свободного конца:

- делаем сечение на первом участке, отбрасываем левую часть, крутящий момент равен моменту внешних сил справа от сечения. Справа внешних моментов нет следовательно крутящий момент равен нулю.

- делаем сечение на втором участке, отбрасываем левую часть, крутящий момент равен моменту внешних сил справа от сечения. Справа приложен момент 2М. Следовательно крутящий момент в сечении на втором участке равен 2М, со знаком минус, согласно правила знаков

М_Z = – 2М.

- делаем сечение на третьем участке, отбрасываем левую часть, крутящий момент равен моменту внешних сил справа от сечения. Справа приложен момент –2М и +3М. Следовательно крутящий момент в сечении на третьем участке равен 1М, со знаком плюс М_Z = +М.

По полученным результатам строим эпюру М_Z – график изменения крутящего момента вдоль вала.

На эпюрах моментов в местах приложения сосредоточенных моментов имеются скачки равные этим моментам.

Величина M_Z в сечении заделки равна M_R – моменту реакции заделки.

При кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.

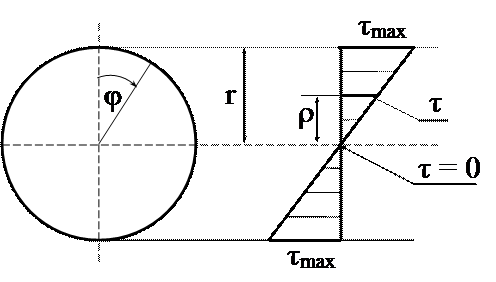
В центре тяжести τ = 0 и Наибольшие напряжения в точках у контура сечения равны:

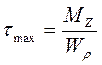
где 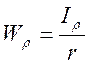- полярный момент момент сопротивления при кручении:

для круга: W_ρ ≈ 0,2·d³

для кольца: W_ρ ≈ 0,2·D³(1-с⁴), где с=d/D;

для квадрата:W_К = 0,208 f, где f – сторона квадрата.

Условие прочности при кручении:

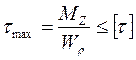
Допускаемые напряжения при кручении:

[τ] = (0,5…0,7)·[σ]р.

Допускаемый крутящий момент:

[M_Z]=W_ρ·[τ]

Определение размеров сечения при кручении:

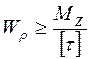
Диаметр круглого вала:

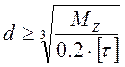
Изгиб

Изгибом называется такое напряженно-деформированное состояние стержня, при котором происходит искривление продольной оси стержня под действием внешних сил.

Стержень, работающий на изгиб, называют балкой. Балка, заделанная одним концом, называется консолью.

Если в поперечном сечении возникает только один ВСФ – изгибающий момент М_И (М_Х или M_Y) – изгиб называют чистым. Если вместе с изгибающим моментом возникает поперечная сила F_y (Q_X или Q_Y) – изгиб называют поперечным.

При изгибе к внешним силам относят: сосредоточенные и распределенные по длине силы, пары сил – моменты и силы реакции опор.

Последние находят из уравнений статики. Исходная схема заменяется расчетной, где опоры заменены силами – реакциями опор.

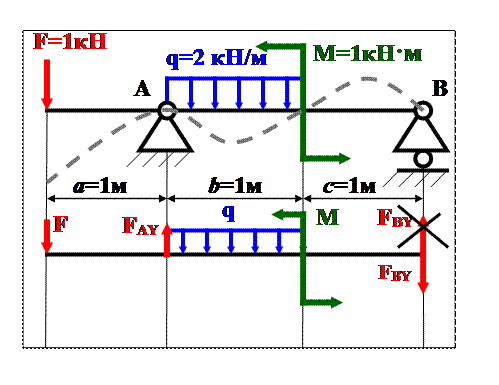
Для расчетной схемы составляются уравнения равновесия, из которых находят силы реакций опор. Рассмотрим пример.

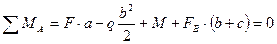
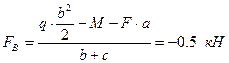
Знак y означает, что реакция в точке В направлена в противоположную сторону. Меняем направление реакции в

точке В. F_B= 0.5 кН

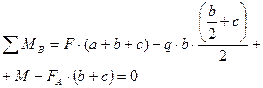
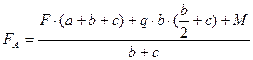
Направление реакции верно.

Обязательная проверка:

∑F_у= – F+ F_А- q·b – F_B=0

-1+3,5+2·1- 0,5=0 0=0

Реакции опор определены верно.

Внутренние силовые факторы при изгибе – изгибающий моментМ_И (М_Х) и поперечную силу Q (F_y) определяют методом сечений.

Поперечная сила Fx,Fy(Q) есть равнодействующая внутренних сил упругости действующих в плоскости поперечного сечения. Она равна алгебраической сумме внешних сил, приложенных перпендикулярно к балке по одну сторону сечения.

Изгибающий момент М_Х, М_У есть момент внутренних сил упругости. Он численно равен алгебраической сумме моментов внешних сил относительно центра тяжести сечения, действующих по одну сторону от данного сечения. Он считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, и отрицательным, если балка изгибается выпуклостью вверх.

Правило знаков.

Наглядное представление о характере изменения ВСФ по длине балки дают эпюры поперечных сил и изгибающих моментов.

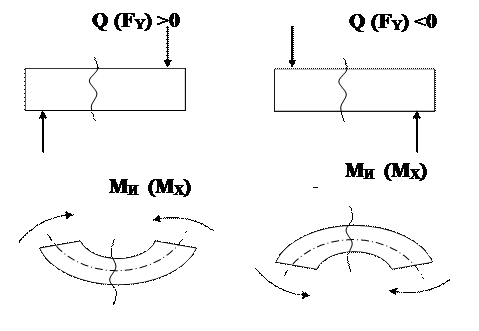
Определим F_y и М_Х в нашем примере и построим их эпюры. Балка имеет 3 характерных участка:

Первый участок: 0≤Z₁≤ a

F_y= - F = - 1 кН

M_X= - F·Z₁

Z₁=0 M_X=0

Z₁=a M_X= – F·a= – 1 кН·м.

Второй участок: а≤Z₂≤ a+в

F_y= - F+ F_А – q·(Z₂ - a);

M_X= - F·Z₂ +F_A·( Z₂ - a) – q·(Z₂ - a)²/2;

Z₂=а F_y= – F+ F_А =2,5 кН;

M_X= – F_A ·a= – 1 кН·м;

Z₂=а+в F_y= – F+ F_А – q·в=0,5 кН;

M_X= – F·(а + в) +F_A·в – q·в²/2=0,5 кН·м.

Третий участок рассмотрим справа налево, т.к. метод сечений рекомендует рассматривать ту часть стержня, к которой приложено меньше внешних сил.

Третий участок: 0≤Z₃≤ с (оси сил расположены противоположно)

F_y= F_В = 0,5 кН;

M_X= - F_В·Z₃

Z₃=0 M_X=0

Z₃=с M_X= - F_В·с= - 0,5 кН·м.

По полученным значениям строим эпюры F_y и М_Х.

Построение эпюр F_y и М_Х позволяет определить напряжения в любом сечении балки. Поперечная сила складывается из элементарных касательных напряжений, а изгибающий момент – из элементарных нормальных напряжений.

Наиболее опасными являются нормальные напряжения при изгибе.

ПЛАКАТ 21

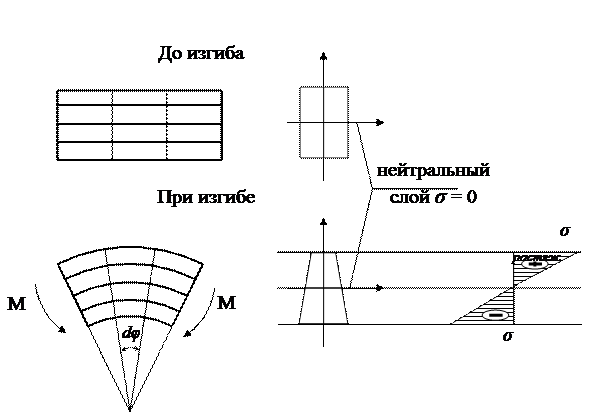
При изгибе волокна на вогнутой стороне укорачиваются – сжимаются, а на выпуклой стороне удлиняются – растягиваются. Между ними существует слой который остается исходной длины – его называют нейтральным слоем;

На нейтральном слое σ = 0. Наибольшие напряжения будут в поверхностных слоях:

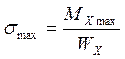
где 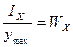– осевой момент сопротивления или момент сопротивления сечения изгибу.

Для круга: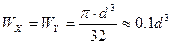

Для прямоугольника: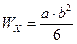

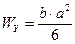
Для прокатных сечений значение W_X дано в сортаменте.

Условие прочности при изгибе:

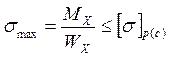
При проектном расчете на прочность при изгибе определяют необходимые размеры сечения через момент сопротивления:

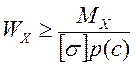
Для круглого сечения W_X=0,1·d³.

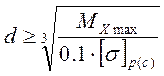
Теории прочности

При объемном напряженном состоянии существуют площадки, по которым действуют только нормальные напряжения. Эти напряжения называют главными:

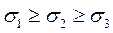
При объемном напряженном состоянии, опыт не может дать однозначный ответ на вопрос «Какое из трех главных напряжений, или какое их сочетание вызывает нарушение прочности – разрушение или текучесть».

Поэтому для составления условий прочности приходится прибегать к гипотезам о причинах нарушения прочности.

Суть применения теорий прочности для оценки прочности материала, заключается в замене фактического напряженного состояния равноопасным (эквивалентным) ему линейным напряженным состоянием.

I теория прочности – теория наибольших нормальных напряжений.

Предполагают, что причиной нарушения прочности является наибольшее из главных напряжений:

σ_max = σ₁ ≤ [σ]

II теория прочности – теория наибольших линейных деформаций.

Предполагают, что причиной нарушения прочности является наибольшая относительная деформация.

ε_max ≤ [ε]

Учитывая, что 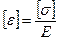, получаем:

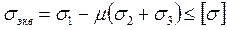
III теория прочности – теория наибольших касательных напряжений.

Предполагают, что причиной нарушения прочности является сдвиг, вызванный касательными напряжениями, при этом условие прочности:

τ_max ≤ [τ]

учитывая что:

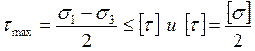
получим:

σ_экв = σ₁ – σ₃ ≤ [σ]

Для плоского напряженного состояния :

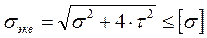
ПЛАКАТ 24

IV теория прочности – энергетическая теория прочности.

Предполагают, что причиной нарушения прочности является потенциальная энергия упругой деформации, накапливающаяся в единице объема материала. Условие прочности имеет вид:

U ≤ [U]

Выразив U и [U] через главные напряжения, получим:

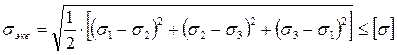
Для плоского напряженного состояния: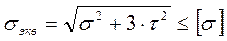

V теория прочности – теория прочности Мора.

Условие прочности:

σ_экв=σ₁ – k·σ₃≤[σ]

где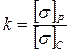

В настоящее время, в практических расчетах используют:

для пластичных материалов – III и IV теории прочности;

для хрупких материалов – теорию прочности Мора.