Метод сечений, внутренние силовые факторы

Сопротивление тел внешним нагрузкам, обуславливается наличием в них внутренних сил, природа которых объясняется теорией атомно-молекулярного строения материи. В СМ не принимаются во внимание внутренние силы, действующие в ненагруженном теле, а рассматриваются только те дополнительные внутренние силы упругости, которые появляются при нагружении тела. Эти силы называют внутренними усилиями или внутренними силовыми факторами (ВСФ).

Для определения ВСФ применяют метод сечений.

Для тела находящегося в равновесии, в интересующем нас месте мысленно делается разрез, например а-а. Затем одна из частей отбрасывается (та, к которой приложено больше сил). Взаимодействие частей друг на друга заменяется равнодействующими внутренними усилиями, которые уравновешивают внешние силы, действующие на отсеченную часть. Если внешние силы лежат в одной плоскости, то для их уравновешивания необходимо, в общем случае, приложить в сечении три внутренних усилия: силу N_Z, направленную вдоль оси стержня, называемую продольной силой, силу Q_Y действующую в плоскости поперечного сечения называемую поперечной силой, и момент М_X называемый изгибающим моментом.

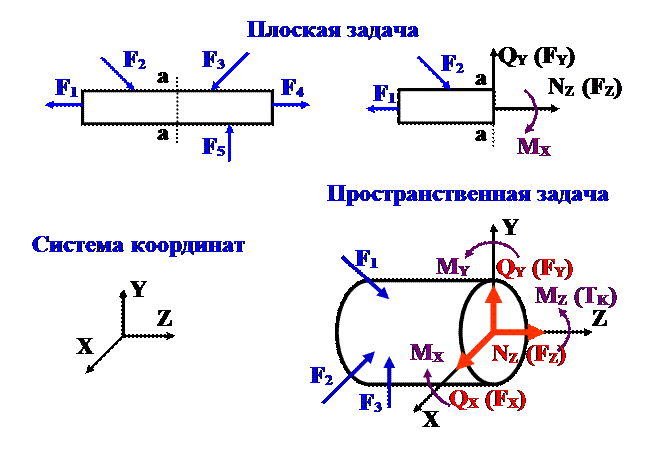
После этого из уравнения равновесия определяют N_Z, Q_Y и М_X .

Для пространственной задачи, когда внешние силы не лежат в одной плоскости, в общем случае могут возникать шесть внутренних усилий:

N_Z ( F_Z) – продольная сила;

Q_X ( F_X) – поперечная сила;

Q_Y ( F_Y) – поперечная сила;

M_Z (T_K) – крутящий момент;

M_X, M_Y – изгибающие моменты.

Они определяются из шести уравнений равновесия.

Алгоритм метода сечений:

1) Разрезать стержень или систему стержней (мысленно);

2) Отбросить одну часть (мысленно);

3) Приложить в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть;

4) Найти значения усилий из уравнений равновесия.

Каждому ВСФ соответствуют свой вид деформации:

1) Растяжение, сжатие – в поперечных сечениях только продольная сила - N_Z ( F_Z);

2) Сдвиг – в поперечных сечениях только поперечные силы Q_X ( F_X), Q_Y ( F_Y);

3) Кручение - в поперечных сечениях только крутящий момент M_Z (T_K);

4) Изгиб - в поперечных сечениях только изгибающие моменты M_X, M_Y;

5) Появление в поперечных сечениях сразу нескольких ВСФ приводит к сложным видам деформации (сложному напряженно-деформированному состоянию).

Напряжения

Внутренние усилия представляют собой статический эквивалент внутренних усилий, распределенных по всей площади сечения.

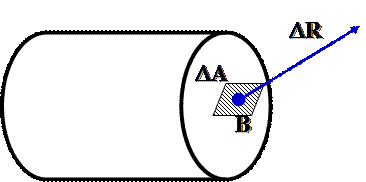
Для определения интенсивности внутренних усилий в данной точке сечения, выделим вокруг точки В малую площадку –. Равнодействующая внутренних усилий, действующих на эту площадку – ΔR, тогда средняя величина внутренних усилий, приходящаяся на единицу площади ΔА рассматриваемой площадки будет равна:

p_ср = ΔR/ ΔА,

уменьшая размеры площадки в пределе получим:

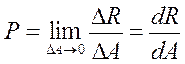
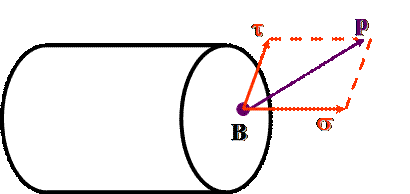
Величина Р называется полным напряжением в точке В.

Его можно разложить на две составляющие:

1) нормальную (перпендикулярную) к плоскости сечения, которая обозначается буквой σ и называется нормальным напряжением;

2) составляющую, лежащую в плоскости сечения, обозначаемую буквой τ и называемую касательным напряжением.

Для удобства τ представляют в виде составляющих по направлению координатных осей τ_X, τ_Y.