Передачи зацеплением с непосредственным контактом
К данному классу передач относятся:
1. Цилиндрические передачи: прямозубые, косозубые и шевронные.
2. Конические передачи с прямыми, косыми и круговыми зубьями.
3. Червячныепередачи с цилиндрическим и глобоидным червяками.
4. Планетарные передачи.
5. Волновыепередачи.
6. Реечныепередачи.
 Наибольшее распространение имеют первые три типа: цилиндрические, конические и червячные. Их используют в большинстве машин для согласования движения при мощностях до 100 МВт и окружных скоростях до 200 м/с.
Наибольшее распространение имеют первые три типа: цилиндрические, конические и червячные. Их используют в большинстве машин для согласования движения при мощностях до 100 МВт и окружных скоростях до 200 м/с.
Достоинства передач зацеплением:
1. Высокий КПД: цилиндрические – (0,96÷0,98); конические – (0,95÷0,97); червячные – (0,7÷0,9);
2. Надежность и долговечность;
3. Компактность и простота в обслуживании.
Недостатки:
1. Шум при работе с большими скоростями.
2. Высокие требования к точности изготовления и монтажа.
3.
Существует два метода нарезания зубьев:
1. Копирование - при котором копируется форма профиля инструмента – дисковой или пальцевой модульной фрезы;
2. Обкатка – при котором воспроизводится зацепление зубчатой пары, одним из элементов которой является режущий инструмент – долбяк, гребенка, червячная фреза.
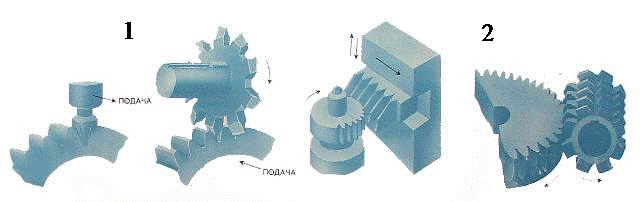
При изготовлении зубчатых колес неизбежны погрешности, которые приводят к повышенному шуму во время работы З.П. и ее преждевременному разрушению.
Стандартом регламентируется 12 степеней точности З.П.: 1, 2…12 в порядке ее убывания.
Наибольшее распространение имеют 6, 7, 8 и 9 степени точности:
| Степень точности ГОСТ 1643-81 | Окружная скорость колес, м/с, не более | Область применения | ||
| Прямозубые | Косозубые | |||
| Скоростные передачи, длительные механизмы | ||||
| Передачи с повышенными скоростями или нагрузками | ||||
| Передачи общего машиностроения | ||||
| Тихоходные передачи низкой точности | ||||
Основные геометрические параметры зубчатого зацепления
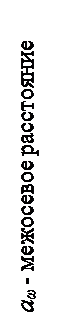

Окружность, на которой шаг Р и угол зацепления соответствуют шагу и углу профиля α инструментальной рейки, называется делительной d. Шаг зубьев Р – расстояние между одноименными профилями соседних зубьев, взятое по дуге делительной окружности P= s + e (толщина зуба + ширина впадины).
s =e - на делительной окружности.
Длина делительной окружности должна соответствовать целому числу зубьев:
π·d=z·P,
следовательно, делительный диаметр равен:
d= z·P /π = m·z
Линейная величина в π раз меньшая шага называется модулем зацепления. Модуль зацепления m – основной параметр зубчатого зацепления, который стандартизирован по ГОСТ 9563-81 (m = 0,05 – 100 мм ).
d1=m·z1 d2=m·z2 – диаметры делительных окружностей;
aω=(d1+d2)/2 = m (z1+ z2)/2 – межосевое расстояние.
Делительная окружность делит зуб по высоте на
головку ha и ножку hf.
ha = m hf =1,25·m
Радиальный зазор с = 0,25·m.
Диаметры окружностей вершин:
da1 = d1 +2·ha= d1 +2·m;
da2 = d2 +2·ha= d2 +2·m.
Окружности впадин:
df1 = d1 - 2·hf= d1 – 2,5·m;
df2 = d2 - 2·hf= d2 – 2,5·m.
У косозубых передач зубья расположены по винтовым линиям, в результате чего зубья входят в зацепления не сразу по всей длине, а постепенно, что значительно снижает шум и динамические нагрузки, повышая нагрузочную способность передачи.
Для нарезания косых зубьев используют тот же инструмент что и для прямых. Наклон зубьев образуют поворотом инструмента относительно заготовки на угол β – угол наклона зубьев (8…15˚).
В этих передачах различают нормальный стандартный модуль mn – модуль в нормальном сечении зубьев и торцевой (окружной) модуль – mt который определяют с точностью до 3-х знаков.

Дата добавления: 2015-12-16; просмотров: 2756;
