Резьбовое соединение группой болтов нагружено

центрально приложенной отрывающей силой N,

перпендикулярной плоскости стыка (рис.43)

Центрально приложенной называют силу N, линия действия которой проходит через центр масс (ц.м.) стыка (опорной части) резьбового соединения.

Сила N равномерно распределяется между всеми предварительно затянутыми болтами соединения, нагружая каждый из них внешней осевой силой 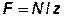, здесь z – число болтов (см. рис. 43).

Рис. 43. Резьбовое соединение группой болтов нагружено центрально приложенной отрывающей силой N, перпендикулярной плоскости стыка

Далее рассматривают единичный болт, предварительно затянутый при сборке силой затяжки F_зат и нагруженный внешней осевой отрывающей силой, перпендикулярной плоскости стыка, как это было рассмотрено в п. 10. 4.

Расчетная сила F_расчна один болт определяется по формуле (31), а внутренний диаметр резьбы d₁ стержня болта по формуле (32).

12. 2. Резьбовое соединение группой болтов нагружено центрально приложенной силой N в плоскости стыка соединяемых деталей (рис. 44)

Сдвигающая сила, нагружающая соединение в районе одного болта:

.

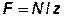Дальнейший расчет проводят по формулам п. 10.3 для единичного болта, установленного с зазором или без зазора.

Рис. 44. Резьбовое соединение группой болтов нагружено центрально приложенной силой N в плоскости стыка соединяемых деталей

12.3. Резьбовое соединение группой болтов нагружено моментом Т в плоскости стыка соединяемых деталей (рис. 45)

Рис. 45. Резьбовое соединение группой болтов нагружено моментом Т в плоскости стыка соединяемых деталей [5]

При решении этой задачи принимают два допущения [5].

Первое. Под действием момента Т соединяемые детали стремятся повернуться друг относительно друга, вращаясь вокруг центра масс (ц. м.) болтового соединения. Такое допущение справедливо для жестких деталей.

Из первого допущения следует условие равновесия:

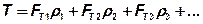. (36)

Второе. Сила, нагружающая соединение в районе каждого болта, пропорциональна расстоянию этого болта от центра масс (ц. м.) болтового соединения – по аналогии с распределением напряжений при кручении круглых цилиндров. При некотором угловом повороте радиуса – вектора перемещение в окружном направлении тем больше, чем дальше от центра масс расположено рассматриваемое сечение. По закону Гука сила пропорциональна перемещению: большему перемещению соответствует большая сила.

Отсюда следует:

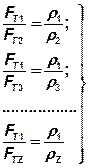(37)

или

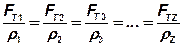. (38)

Для примера на рис. 45:

Для нахождения этих сил на основании условий (36) и (37) запишем:

Таким образом, в групповом соединении под воздействием момента Т в плоскости стыка наиболее нагруженной оказывается зона болта, находящегося на наибольшем расстоянии от центра масс соединения. Дальнейший расчет проводят по формулам п. 10.3 для единичного болта, нагруженного наибольшей сдвигающей силой F_T, в зависимости от того, как установлен болт: с зазором или без зазора.

12.4. Резьбовое соединение группой болтов нагружено комбинацией сил и моментов в плоскости стыка соединяемых деталей (рис. 46)

Исходное условие – групповое болтовое соединение нагружено консольной силой N, действующей в плоскости стыка соединяемых деталей (рис. 46).

Приложим силу N к центру масс (ц. м.) болтового соединения и уравновесим ее равной по величине силой N' противоположного направления. Заменим пару сил, отмеченных двумя черточками, моментом .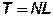

Таким образом, после приведения силы к центру масс соединения, выяснилось, что оно нагружено центрально приложенной сдвигающей силой N и моментом T в плоскости стыка.

Рис. 46. Резьбовое соединение группой болтов нагружено комбинацией сил и моментов в плоскости стыка соединяемых деталей [5]

Далее в соответствии с принципом независимости действия сил от каждого силового фактора находят составляющие с последующим их геометрическим суммированием.

Составляющая F_Т от момента Т перпендикулярна радиусу 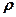, проведенному из центра масс (ц. м.) к оси болта. Момент, создаваемый силой F_Т направлен навстречу моменту Т.

Для определения F_Т составляется система уравнений (36) и (37) (см. п. 12.3).

Для примера на рис. 46:

Для нахождения составляющих F_Т от момента Т на основании условий (36) и (37) запишем:

Решение данной системы с двумя неизвестными позволяет определить составляющие F_Т1 и F_Т2 , а затем и остальные F_Т3, F_Т4, F_Т5 и F_Т6.

Составляющая от центрально приложенной сдвигающей силы N:

,

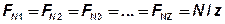здесь z – число болтов.

Направление составляющей F_N противоположно направлению силы N.

Суммарная сила, нагружающая соединение в районе каждого болта:

.

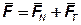В рассматриваемом на рис. 46 случае наиболее нагружены соединения в районе болтов 1 и 3 (F_Т1 и F_Т3 – максимальные, углы между векторами составляющих сил – острые) или болта 2 (меньшее значение F_Т2 , но угол между векторами сил равен нулю).

Дальнейший расчет проводят по формулам п. 10.3 для единичного болта, нагруженного сдвигающей силой F, в зависимости от того, как установлен болт: с зазором или без зазора.

12.5.Резьбовое соединение группой болтов нагружено отрывающей и сдвигающей силами, а также опрокидывающим моментом (на примере крепления кронштейна к плите или раме) (рис. 47) [5]

На рис. 47, а показана схема нагружения кронштейна, на рис. 47, б – форма опорной поверхности кронштейна (форма стыка), на рис. 47, в – эпюры напряжений на стыке.

Рис. 47. Резьбовое соединение группой болтов нагружено отрывающей и сдвигающей силами, а также опрокидывающим моментом [5]

Первоначально кронштейн закреплен на основании четырьмя (в общем случае z) болтами, а затем нагружен внешней силой N.

Центр масс (ц. м.) болтового соединения расположен в плоскости стыка на пересечении осей x, y симметрии опорной поверхности. Для удобства дальнейшего рассмотрения разложим силу N на составляющие: вертикальную отрывающую 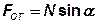и горизонтальную сдвигающую 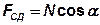. Приведем полученные составляющие к центру масс (ц. м.) болтового соединения. В соответствии с правилами теоретической механики сила 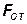может быть перенесена вдоль линии своего действия до центра масс. Приложим силу 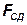к центру масс и уравновесим ее равной по величине силой 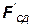противоположного направления. Отмеченную черточками пару сил заменяем моментом: .

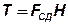После приведения сил в центр масс болтового соединения выяснилось, что кронштейн нагружен центральной отрывающей силой 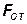, сдвигающей силой 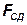и опрокидывающим моментом Т.

Действие отрывающей силы 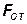и опрокидывающего момента T уменьшает напряжения на стыке от предварительной затяжки – может произойти раскрытие стыка.

Под действием сдвигающей силы 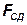может произойти сдвиг деталей.

Таким образом сила затяжки болтов в данном случае должна обеспечить выполнение двух условий: нераскрытие стыка и несдвигаемость стыка.

Определение силы затяжки F_зат болтов из условия нераскрытия стыка.Рассмотрим напряжения на стыке от действующих силовых факторов F_зат, F_oт и Т.

Каждый из z болтов предварительно затянут с силой F_зат, т.е. кронштейн предварительно нагружен суммарной силой zF_зат. Предполагаем, что напряжения σ_зат сжатия на стыке деталей от силы затяжки распределены равномерно (рис. 47, в):

,

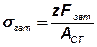где 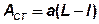- площадь стыка (рис. 47, б).

Отрывающая сила 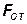разгружает стык на 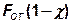(см. п.10.4). Значит, напряжения сжатия на стыке от действия силы 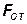уменьшаются на

,

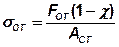где 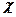- коэффициент внешней нагрузки, определяемый по формуле (27).

При достаточно большой силе предварительной затяжки F_зат (а именно такая сила может обеспечить нераскрытие стыка) и жестких фланцах поворот опорной поверхности кронштейна под действием опрокидывающего момента T происходит относительно оси y симметрии стыка, так как относительно этой оси наименьший момент сопротивления повороту (наименьший момент инерции площади стыка). Пока стык не раскрылся, кронштейн и основание можно рассматривать как единое целое.

Поворот кронштейна вызывает изменение напряжений пропорционально расстоянию от нейтральной оси y, т.е. по закону изгиба. В соответствии с законом изгиба наибольшие напряжения σ_МОМ действуют на наиболее удаленном волокне, т.е. в точках А и В.

С учетом того, что на стык приходится только часть внешнего опрокидывающего момента (согласно п.10.4 ) 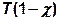, то напряжения σ_МОМ:

,

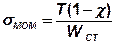где 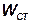- момент сопротивления стыка:

.

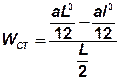Действие опрокидывающего момента Т изменяет напряжения сжатия на стыке (рис. 47, в): в одной части стыка увеличивает эти напряжения, в другой уменьшает.

О выполнении условия нераскрытия стыка судят по наименьшим напряжениям сжатия на суммарной эпюре в точке А:

.

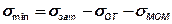При 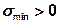условие нераскрытия стыка выполнено. В практических расчетах обычно вводят некоторый запас, принимая значения 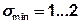Н/мм² для пары сталь (чугун) – сталь (например, крепление редуктора на раме) или 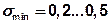Н/мм² для пары сталь (чугун) – бетон (например, крепление узлов на бетонном полу цеха).

По задаваемому таким образом значению минимальных допускаемых напряжений на стыке 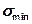находят необходимые напряжения от силы затяжки:

.

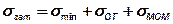Полученное значение 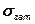позволяет рассчитать предварительную силу затяжки F_зат каждого болта, обеспечивающую нераскрытие стыка:

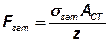. (39)

Следует отметить, что форма стыка оказывает влияние на нагруженность болта. Оптимальной является форма стыка с малой площадью опорной поверхности и большим моментом инерции относительно оси y. Иначе говоря, опорную поверхность кронштейна желательно выполнять в виде отдельных платиков в районе установки болтов, а сами болты располагать в пределах габаритов изделия на возможно большем расстоянии от оси y.

Так как в точке В возникают наибольшие напряжения сжатия на стыке, то в этой точке следует проверить прочность основания по напряжениям смятия:

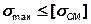
или

.

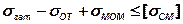Для бетона 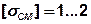Н/мм².

Определение силы затяжки болтов F_зат из условия несдвигаемости стыка.Как и в предыдущем случае, кронштейн нагружен предварительной суммарной силой затяжки zF_зат.

Условие несдвигаемости выполнено, если сила трения F_тр больше сдвигающей силы F_СД . С учетом коэффициента 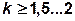запаса по несдвигаемости имеем

.

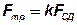По общему определению сила трения – произведение нормальной к поверхности контакта силы F_n и коэффициента трения :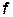

.

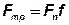В рассматриваемом случае крепления кронштейна сила F_n равна:

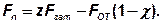
Тогда условие несдвигаемости стыка принимает вид:

.

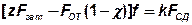Отсюда получаем зависимость для определения силы затяжки F_зат , обеспечивающей несдвигаемость стыка:

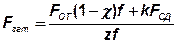. (40)

Для обеспечения работоспособности соединения одновременно по двум критериям необходимо принять силу затяжки F_зат одного болта, равную большему значению из двух, полученных по формуле (39) и (40). При этом будет обеспечено выполнение как условия нераскрытия, так и несдвигаемости стыка.

Для определения расчетной силы на болт F_расч, кроме силы затяжки F_зат, необходимо знание той части внешней нагрузки, которая дополнительно нагружает каждый болт. Так как внешней нагрузкой для болтов является отрывающая сила F_ОТ и опрокидывающий момент Т, то осевые нагрузки от них на каждый болт равны:

а) от отрывающей силы F_ОТ:

;

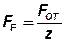б) от опрокидывающего момента Т внешнюю осевую нагрузку на один болт F_Т определяем из условия равновесия:

,

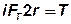где 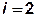- число болтов в поперечном ряду.

Отсюда .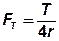

Тогда часть внешней нагрузки, которая дополнительно нагружает каждый болт равна

.

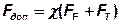Расчетная сила F_расч на каждый болт будет складываться из силы предварительной затяжки F_зат с учетом момента сил трения в резьбе, скручивающего стержень при затяжке (коэффициент 1,3) и части внешней нагрузки F_доп, которая дополнительно нагружает болт:

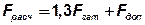
или

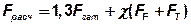
При проектном расчете определяют d₁ резьбы болта

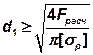
а по нему подбирают резьбу.