Особое внимание следует обратить на построение системы показателей и определение совокупности факторов, влияющих на каждый из показателей.

Множественная регрессия и корреляция

Eравнение множественной регрессии

,

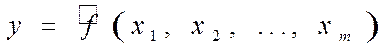где 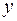– зависимая переменная (результативный признак), 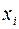– независимые, или объясняющие, переменные (признаки-факторы).

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетахи целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Особое внимание следует обратить на построение системы показателей и определение совокупности факторов, влияющих на каждый из показателей.

- включение каждого фактора в модель должно быть обосновано теоретически;

- целесообразно учитывать только те факторы, которые оказывают существенное влияние на изучаемые показатели, при этом рекомендуется, чтобы количество включаемых в модель факторов не превышало одной трети от числа наблюдений в выборке (длины временного ряда);

- между факторами не должно существовать линейной зависимости, поскольку ее наличие будет означать, что они характеризуют влияние одной и той же по сути причины на показатель.

Например, размер заработной платы работников зависит, в том числе и от роста производительности труда и от объема выпускаемой продукции. Однако эти два фактора могут быть тесно взаимосвязаны, коррелированны, следовательно, в модель целесообразно включить лишь один из них;

- в модель рекомендуется включать только те факторы, которые могут быть измерены количественно;

- в одну модель не следует включать какой-либо фактор одновременно с образующими его частными факторами. Это приведет к не соответствующему реальности увеличению их влияния на зависимые переменные модели и, как следствие, к искажению отображения реальной действительности.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором 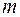факторов, то для нее рассчитывается показатель детерминации 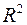, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии 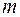факторов. Влияние других, не учтенных в модели факторов, оценивается как 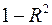с соответствующей остаточной дисперсией .

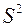При дополнительном включении в регрессию 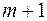фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:

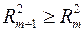и .

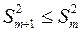Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор 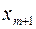не улучшает модель и практически является лишним фактором.

Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 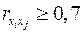. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

1. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл.

2. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 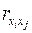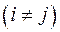были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных

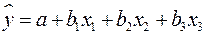
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:

.

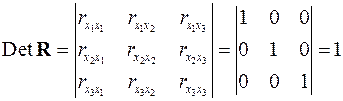Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:

.

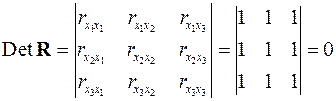Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.

Итак. Имеем функцию 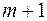аргумента: .

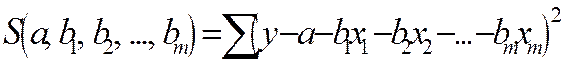Находим частные производные первого порядка:

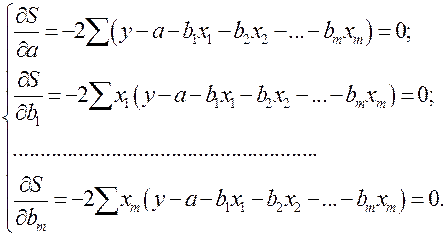
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2.1):

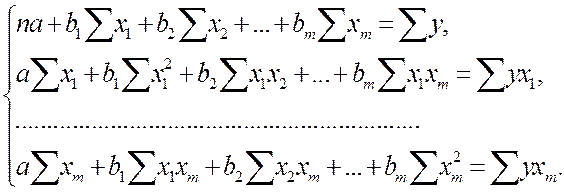
Для двухфакторной модели данная система будет иметь вид:

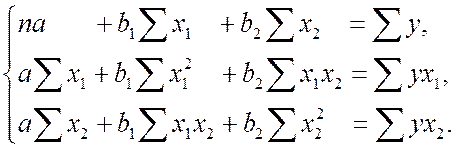
Рассмотрим линейную модель множественной регрессии

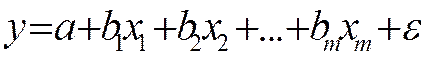
Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 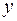от расчетных 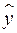минимальна:

.

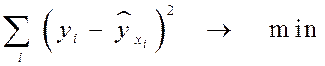Рассмотрим пример[1] (для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего 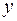(т), мощности пласта 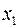(м) и уровне механизации работ 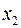(%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 2.2

№	1	2	3	4	5	6	7	8	9	10

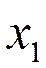
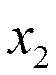
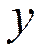
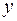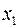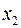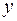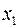Предполагая, что между переменными , , существует линейная корреляционная зависимость, найдем уравнение регрессии по и .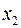

Для удобства дальнейших вычислений составляем таблицу ( ):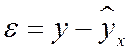

Таблица 2.3

№
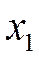
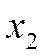
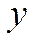
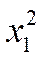
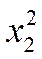
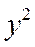
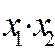
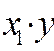
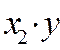
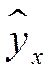
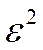
										5,13	0,016
										8,79	1,464
										9,64	0,127
										5,98	1,038
										5,86	0,741
										6,23	0,052
										6,35	0,121
										5,61	0,377
										5,13	0,762
										9,28	1,631
Σ											6,329
Ср. знач.	9,4	6,3	6,8	90,8	41,7	49,6	60,3	66,4	44,5	–	–
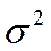
	2,44	2,01	3,36	–	–	–	–	–	–	–	–
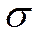
	1,56	1,42	1,83	–	–	–	–	–	–	–	–

Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:

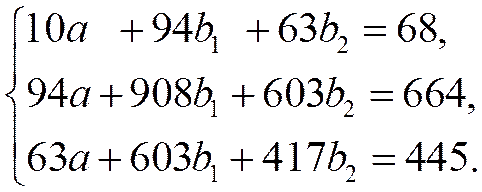
Откуда получаем, что ,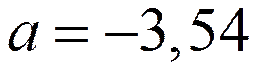

,

.

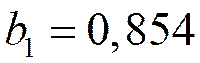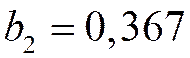Т.е. получили следующее уравнение множественной регрессии:

.

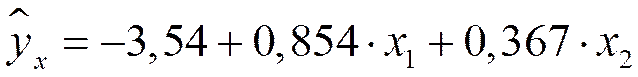Оно показывает, что при увеличении только мощности пласта 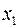(при неизменном 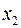) на 1 м добыча угля на одного рабочего 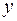увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ 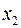(при неизменном 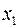) на 1% – в среднем на 0,367 т.

Найдем уравнение множественной регрессии в стандартизованном масштабе:

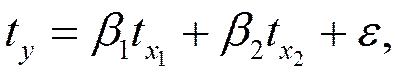
при этом стандартизованные коэффициенты регрессии будут

,

.

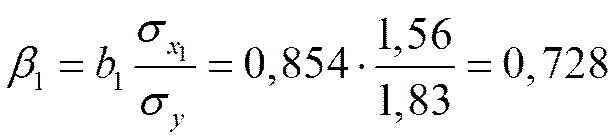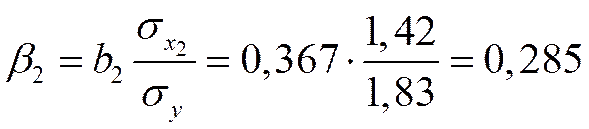Т.е. уравнение будет выглядеть следующим образом:

.

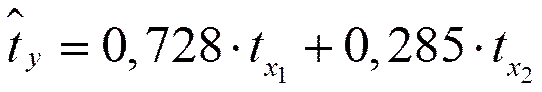Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что мощность пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):

.

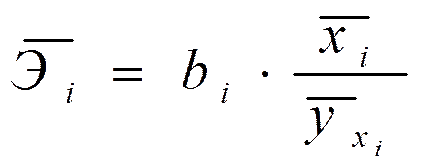Вычисляем:

, .

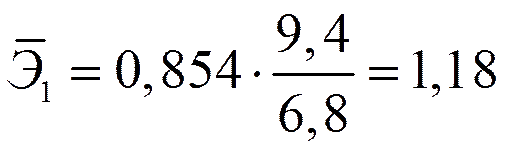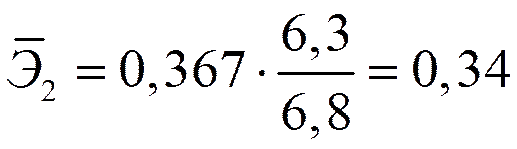Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат 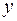фактора 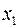, чем фактора .

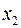[1] Данные примера взяты из [5]