Усиление света в активной среде лазера
Обратимся теперь к вопросу о том, как и при каких условиях возможно усиление света за счет вынужденного излучения. Вычислим изменение интенсивности света при прохождении им слоя вещества.
Рис.5.
Пусть плоская световая волна частоты w, резонансной некоторому квантовому переходу, падает на слой вещества толщиной dz (рис.5а). Выделим некоторую площадку s на поверхности слоя и рассмотрим элемент среды объемом dV=sdz. Обозначим число атомов в единице объема среды через N. Тогда число атомов в рассматриваемом элементе среды составляет dN=NdV. При этом на нижнем энергетическом уровне находится dN1=N1dV атомов, а на верхнем - dN2=N2dV атомов, где Ni - число атомов на соответствующем уровне i, отнесенное к единице объема.
Используя модель Эйнштейна, запишем мощности спонтанного излучения dP21спонт, вынужденного излучения dP21вын для данного элемента среды в виде
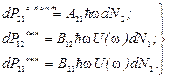(16)
Здесь U(w) - спектральная мощность падающего излучения на частоте w; hw - энергия кванта; А21 - вероятность спонтанного излучения кванта света атомом в единицу времени; В12 - вероятность вынужденного поглощения кванта света атомом в поле излучения единичной спектральной плотности за единицу времени; В21 - вероятность вынужденного испускания кванта света атомов в поле излучения единичной спектральной плотности за единицу времени. По существу, формулы (16) можно рассматривать как определения коэффициентов А21, В12, В21.
Полная мощность излучения данного элемента среды есть
dP = dP21спонт + dP21вын - dP12вын. (17)
Используя, для простоты, прямоугольную аппроксимацию спектра излучения (рис.5б), нетрудно показать, что для плоской волны интенсивность I и спектральная плотность U света связаны между собой соотношением
I=c·U·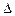 
w , (18)
где 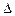w - ширина спектра; с - скорость света.
Из (16) - (18) для приращения интенсивности света dI получаем выражение
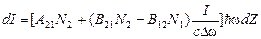. (19)
Теперь предположим, что интенсивность света достаточно велика, чтобы можно было пренебречь спонтанным излучением, и введем обозначение В12=В21=В. Тогда из (19) следует, что
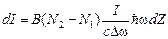(20)
или в более компактной записи:
dI = G·I·dZ, (21)
где
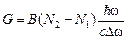. (22)
Из (21) находим закон изменения интенсивности света по мере увеличения расстояния z, пройденного в среде
I(z) = I0·eGz (23)
Вывод: интенсивность света в среде меняется по экспоненциальному закону, причем знак показателя экспоненты зависит от знака разности населенности уровней N2-N1.
Вариант 1. Среда в обычном состоянии теплового равновесия
В соответствии с формулами (1) и (2) отношение населенностей уровней выражается формулой
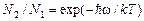. (24)
Оценим величину параметра hw/kT для видимого диапазона частот и комнатной температуры. Полагая Т=300К; w=2pc/l, l=0,5*10-4см; с=3*1010см/с; k=1,38*10-16эрг/К;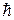 
=1,05*10-27эрг . с - получим:
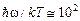(25)
Из (24) и (25) следует, что тепловой заселенностью верхнего рабочего уровня можно пренебречь. Полагая N1=N, N2=0, получим из (22) и (23)
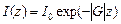, (26)
где
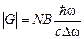. (27)
Очевидно, что формула (26) описывает обычное поглощение света в среде (закон Бугера).
Вариант 2. Квантовая модель неравновесной среды
Квантовая модель предсказывает возможность экспоненциального усиления света в среде. Согласно (22) для этого необходимо, чтобы населенность верхнего рабочего уровня превышала населенность нижнего уровня
N2>N1 (28)
т.е. чтобы имела место инверсия населенностей. Именно этот эффект используется в лазере.
Таким образом, мы видим, что в случае термодинамического равновесия N2<N1. Такая среда поглощает излучение на частоте w, что обычно и происходит. Однако, если удается достигнуть неравновесного состояния, для которого N2>N1, то среда будет действовать как усилитель. В этом случае говорят, что в среде существует инверсия населенностей, имея в виду, что разность населенностей (N2-N1)>0 противоположна по знаку той, которая существует в обычных условиях (N2-N1)<0.
Среду, в которой осуществлена инверсия населенности, называют активной средой.
Дата добавления: 2015-12-16; просмотров: 878;