Ламинарное течение жидкости в трубе. Формула Пуазейля

Рассмотрим стационарный поток жидкости, ламинарно текущей через капилляр круглого сечения (рис. 5)

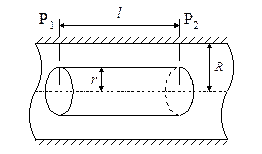
Рис. 5. К выводу формулы Пуазейля.

Мысленно выделим в жидкости цилиндр радиуса r и длины l. Обозначим давление на его торцах через Р₁ и Р₂. При ламинарном течении сила давления (Р₁-Р₂)pr² уравновешивается силой вязкого трения, действующей на цилиндр со стороны наружных слоев жидкости. Эта сила равна 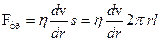, где s=2prl – поверхность цилиндра, h – вязкость, dv/dr – градиент скорости. Приравнивая к нулю сумму сил, действующих на цилиндр, получим

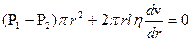. (7)

Интегрируя это равенство и учитывая очевидное граничное условие 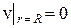, получим

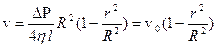, (8)

где v₀ = 2v_ср – осевая, численно максимальная скорость течения, v_ср – средняя по расходу скорость жидкости. Таким образом, скорость жидкости квадратично меняется с радиусом и максимальна на оси трубки (см. рис. 2).

Расход жидкости Q, т.е. объем, ежесекундно протекающий через поперечное сечение трубки, равен

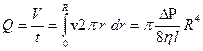. (9)

Формула (9) носит название формулы Пуазейля. Она показывает, что вязкость жидкости можно определить, измеряя ее расход Q, перепад давления DP, длину трубки и ее радиус.

Соотношение (9) используется для определения вязкости жидкостей методом Пуазейля. Пропуская жидкость через капилляр известного радиуса, измеряя перепад давления и поток Q, можно найти h.

Формула Пуазейля применима только к ламинарному течению жидкости. Для определения характера течения жидкости вычислим число Рейнольдса из общей формулы (6)

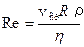, (10)

где r – плотность жидкости. Если Re <Re_кр, то течение в данной трубке можно считать ламинарным. В гладких трубках круглого сечения Re_кр»1100.

Ламинарное движение жидкости при переходе ее из широкого сосуда в капилляр устанавливается не сразу, а после того, как она пройдет расстояние а:

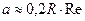. (11)

Формула (9) дает надежные результаты лишь в том случае, если длина капилляра во много раз больше а.