Динамики микрочастиц

Первоначально возникли две отличающиеся по форме квантовые теории. В одной из них - волновой механике Шредингера - состояние микрочастицы описывается не положением и скоростью в какой-то момент времени (как в механике Ньютона), а непрерывной комплексной функцией координат и времени Y (r, t), которую называют «пси-функцией». Физический смысл этой функции состоит в том, что квадрат ее модуля ïY(r, t)½² в каждый момент времени определяет вероятность нахождения микрочастицы вблизи точки пространства с радиус-вектором r (рис. 7.4). Таким образом, в волновой механике с самого начала отказались от наглядного описания движения частиц с помощью траекторий. Более того, волновая механика является не динамической теорией, позволяющей однозначно предсказать положение и скорость микрочастицы в любой момент времени, а статистической теорией, определяющей вероятности, с которыми наблюдаемые величины имеют те или иные значения.

Динамика микрообъектов описывается в волновой механике с помощью так называемого уравнения Шредингера, которое представляет собой дифференциальное уравнение 2-го порядка в частных производных для Y- функции и имеет такое же значение, какое в классической механике имело уравнение F = ma.

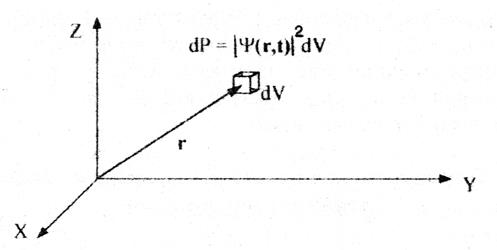
Рис. 7.4. Физический смысл Y-функции.

dP - вероятность обнаружить микрочастицу в малом объеме dV.

В другой квантовой теории - квантовой механике Гейзенберга, Борна и Иордана - состояние микрообъекта описывается упорядоченным набором комплексных чисел (комплексным вектором), а той или иной динамической характеристике (координата, импульс, момент импульса и др.) соответствуют операторы, воздействующие на этот вектор. Математически такие операторы описываются матрицами, поэтому другое название этой теории - матричная механика. Эта механика полностью эквивалентна волновой механике Шредингера, хотя обе теории используют разный математический формализм.

Отличие квантовых, а также релятивистских подходов от классических представлений было настолько велико, что XX в. стал прочно ассоциироваться с новым этапом в естествознании, который сейчас называют неклассическим. Отметим некоторые наиболее важные особенности этого этапа.

1. Если в классическом естествознании статистические закономерности относились к поведению больших ансамблей идентичных объектов, в то время как динамика отдельных объектов оставалась строго детерминированной, то в неклассическом естествознании вероятностный подход «спускается» на уровень индивидуальных объектов. О том, насколько сложным и «болезненным» был переход к неклассическим идеям в этом вопросе, свидетельствуют высказывания самих отцов квантовой теории. Эйнштейн незадолго до своей смерти писал: «Если статистическая квантовая теория не претендует на полное описание индивидуальной системы (и ее поведение во времени), то попытки найти это полное описание где-то еще, провидимому, неизбежны… С учетом этого приходится признать, что указанная схема в принципе не может служить базисом теоретической физики». Луи де Бройль также считал, что «¼возможно, в один прекрасный день окажется, что квантовая теория дает нам лишь статистическое определение аспектов лежащей за ним физической реальности, которую она не в состоянии описать полностью». Однако, впоследствии выяснилось, что индивидуально - статистический подход к поведению микрообъектов является единственно возможным и отражает непосредственную «ненаблюдаемость» их движения.

2. Если для классического объекта в принципе можно измерить все его динамические параметры, то для микрообъектов этого в общем случае сделать нельзя. В методологическом отношении данное обстоятельство привело к формулировке принципа дополнительности Бора, который в настоящее время имеет общекультурное значение. Согласно этому принципу, получение экспериментальной информации об одних физических величинах, описывающих микрообъект, неизбежно связано с потерей информации о некоторых других величинах, дополнительных к первым. Такими взаимно дополнительными величинами являются, например, координата микрочастицы и ее скорость. С физической точки зрения принцип дополнительности часто объясняют (следуя Бору) влиянием «измерительного прибора» (который всегда является макроскопическим объектом) на состояние микрообъекта. При точном измерении одной из дополнительных величин с помощью соответствующего прибора другая величина в результате взаимодействия микрообъекта с прибором претерпевает неконтролируемые изменения. Можно, однако, показать, что даже в отсутствие измерительного прибора дополнительные величины не могут одновременно иметь абсолютно точные значения.

Частным случаем принципа дополнительности является принцип неопределенности Гейзенберга, одна из эквивалентных формулировок которого заключается в следующем: произведение неопределенности координаты микрочастицы Dх и неопределенности соответствующей проекции ее импульса D 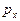не превышает значения постоянной Планка h.

3. Отказ от классических традиций произошел также в том, что в науку стали вводиться величины (например, Y - функция), сами по себе не являющиеся непосредственно измеряемыми. В дальнейшем эта тенденция стала преобладающей.