Поле электрического диполя.

Электрическим диполем называется элементарный электрический вибратор, размеры которого много меньше излучаемой им длдины волны, по которому протекает переменный во времени и постоянный по величине электрический ток и поле которого исследуется на расстоянии z>>e

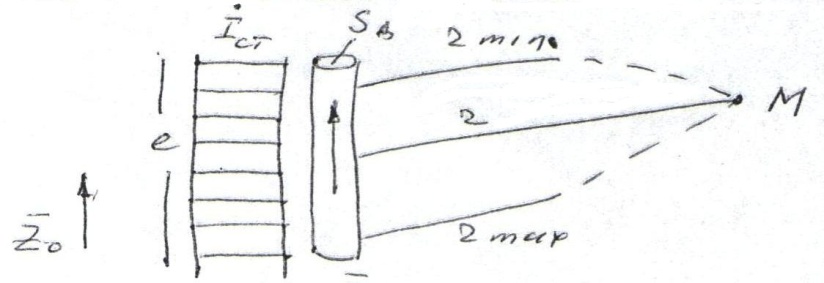
При z>>e δ z_min≈z≈z_max

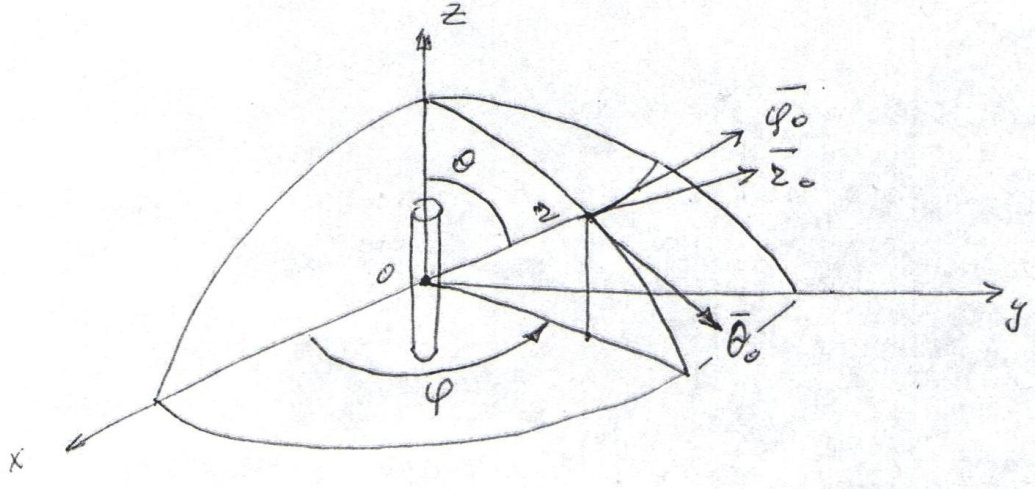
Анализ поля удобно проводить в сферической системе координат. Поставленная задача относится к числу тех, когда целесообразно определить векторный потенциал 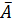, а затем уже найти 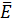и

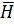
Вычислим векторный потенциал поля в точке М.

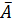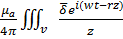= d(esд) (1)

Плотность тока 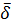неизменна по длине диполя z, z также величина постоянная в силу удаленности точки М.

Тогда

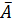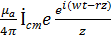
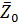= (2) ( )!

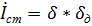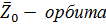
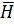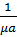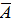На основании известного соотношения = rot и rot 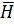= iwԐ_a 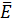запишем

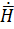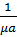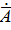
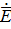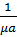= rot

= rot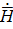

Следовательно напряженность магнитного поля диполя определяется вихрем первого порядка векторного потенциала (rot 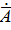), а напряженность электрического поля- вихрем второго порядка (rot rot )

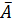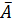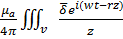= de*sд

Перепишем (2) в сферических координатах

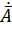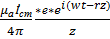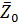= ( cosθ- 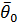sinθ) (3)

Или

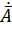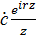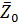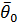= ( cosθ- sinθ)

гд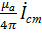е = е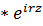

тогда

rot 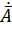=[ 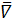* 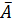] = 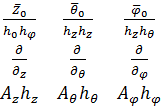(4)

Где 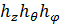- коэффициенты Ламэ для сферической системы координат ( 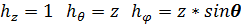), а проекции вектора 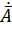равны

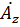=c*cosθ*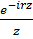

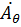=-c*sinθ*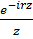

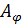=0

Вычисляя определитель (4) и возвращаясь к 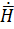= 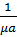rot 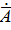получаем

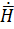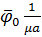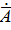= rot (5)

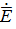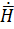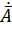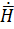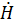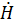С целью нахождения аналитического выражения для напряженности электрического поля необходимо определить rot Для этого следует повторить вычисления определителя (4) , заменив в нем проекции на проекции Из (5) следует, что ₂= ₀=0

Результатом вычислений является выражение

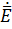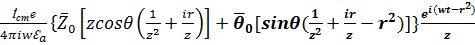= (6)

Выражения (5) и (6) позволяют рассчитать напряженности поля всюду вокруг электрического диполя ( при z>>e)

Анализ выражений (5) и (6) показывает, что 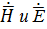содержат слагаемые, по –разному зависящие от z

Поэтому в зависимости от удаленности точки М от диполя определяющий вклад в величины 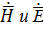будут вносить разные слагаемые. В зависимости с этим принято выделять ближнюю, промежуточную и дальнюю зоны поля диполя.