Элементарная теория активных столкновений для бимолекулярных реакций
В основе теории лежит положение о том, что реакция осуществляется при столкновении молекул, поэтому скорость химической реакции должна быть пропорциональна числу сталкивающихся молекул в единице объема за единицу времени.
Согласно молекулярно-кинетической теории число соударений Zо одинаковых молекул в 1 см3 газа за 1 с равно
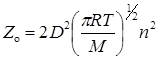 см–3·с–1, (21.1)
см–3·с–1, (21.1)
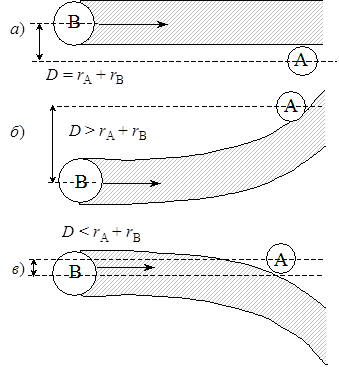 Рис. 21.1. Схема столкновений между двумя молекулами: а) отсутствие взаимодействия; б) притяжение; в) отталкивание
Рис. 21.1. Схема столкновений между двумя молекулами: а) отсутствие взаимодействия; б) притяжение; в) отталкивание
|
где n – концентрация (число молекул в 1 см3), M – молярная масса, D – газокинетический диаметр (диаметр столкновений).
В случае идеального газа, т.е. при отсутствии взаимодействия, D равен сумме радиусов сталкивающихся частиц – D = r1 + r2 или для одинаковых частиц D = 2r. Фактически же в реальных системах, где пренебречь взаимодействием нельзя, для столкновения необходимо, чтобы частицы находились на некотором расстоянии D < 2r, если между ними действуют силы отталкивания, или D > 2r, если действуют силы притяжения (рис. 21.1). В связи с этим величина D представляет эффективный диаметр столкновений.
Число столкновений разных молекул 1 и 2
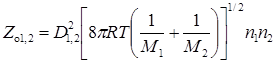 см–3·с–1. (21.2)
см–3·с–1. (21.2)
Если при каждом соударении происходит акт химического взаимодействия, то скорость реакции должна быть равной величине Zo или Zo1,2. Однако экспериментальные данные указывают на то, что действительные скорости реакций на несколько порядков ниже, чем рассчитанные по числу столкновений. Например, в реакции разложения йодистого водорода HI + HI ® H2 + I2 при 556 К и концентрации 1 моль HI в 22,4 л газовой смеси число сталкивающихся молекул равно примерно 1×1029 см–3с–1, число же молекул, которые реагируют, полученное из эксперимента, равно 4×1011 см–3 с–1. Отсюда можно сделать вывод о том, что не всякое столкновение активно, т.е. приводит к акту химического взаимодействия.
Существует несколько причин снижения эффективности соударений. Например, при столкновении простых атомов или радикалов может образоваться колебательно-возбужденная молекула, обладающая избыточной энергией, поэтому такая молекула существует очень короткое время. Наиболее вероятным путем стабилизации является передача избыточной энергии третьему телу – другой молекуле, стенкам сосуда и т.п. Если время до соударения с третьим телом превышает время жизни колебательно-возбужденной молекулы, она распадается на исходные частицы. Другой причиной снижения эффективности является необходимость определенной ориентации в пространстве при реакции между сложными молекулами. Чтобы реакция осуществилась, молекулы должны сближаться своими активными, реакционноспособными группами. В качестве характеристики снижения эффективности за счет пространственной ориентации используется стерический множительР, величина которого может изменяться в пределах примерно от 10–5 до 1. В теории активных соударений нет методов вычисления стерического множителя, и его оценивают при сравнении рассчитанной и определенной из опыта скоростей.
Однако основной причиной, снижающей эффективность соударений, является энергетический фактор. Для того чтобы прошел элементарный акт взаимодействия, необходимо преодолеть силы отталкивания, возникающие при сближении молекул, ослабить или разрушить межатомные связи в молекуле так, чтобы соответствующие атомы могли сблизиться и образовать новые связи. Для этого необходима значительная энергия – энергия активации.
Таким образом, с точки зрения теории столкновений, энергия активации – это минимально необходимая энергия, которой должна обладать молекула в момент столкновения, чтобы прореагировать. Такую энергию могут иметь молекулы с повышенной кинетической энергией поступательного движения или молекулы, атомы которых находятся на более высоких энергетических уровнях – активные молекулы.
В простейшем случае теории для бимолекулярных реакций рассматривается относительная кинетическая энергия молекул вдоль линии, соединяющей их центры. Скорость реакции считается равной числу активных столкновений Z; число таких столкновений между молекулами, кинетическая энергия движения которых вдоль линии центров равна или больше энергии активации E, будет равно в соответствии с законом распределения Больцмана
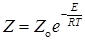 . (21.3)
. (21.3)
С учетом уравнений (21.1) или (21.2) скорость реакции равна
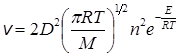 см–3·с–1. (21.4)
см–3·с–1. (21.4)
или
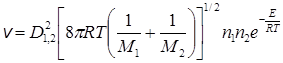 см–3 ·с–1. (21.5)
см–3 ·с–1. (21.5)
Запишем кинетическое уравнение для скорости реакции через константу скорости:
v = kn2 или v = kn1n2. (21.6)
Сравнивая эти уравнения с выражениями (21.4) и (21.5), получим для константы скорости реакции:
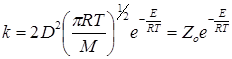 (21.7)
(21.7)
для реакции между одинаковыми молекулами или
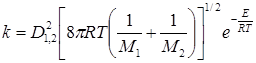 (21.8)
(21.8)
для реакции между разными молекулами.
Таким образом, общее теоретическое уравнение для константы скорости бимолекулярной реакции можно записать в виде произведения предэкспоненциального множителя и экспоненты:
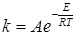 . (21.9)
. (21.9)
которое по форме совпадает с уравнением Аррениуса (20.98). Теория активных соударений не дает возможности вычисления истинной энергии активации E, поэтому при сопоставлении теории с экспериментом можно сравнивать или предэкспоненциальные множители или брать опытную величину энергии активации E при расчете констант скорости.
Установим связь между истинной E и опытной EA энергиями активации. Для этого представим уравнения (21.7) или (21.8) в форме
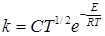 , (21.10)
, (21.10)
где С включает все постоянные, и прологарифмируем его:
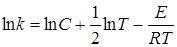 . (21.11)
. (21.11)
Дифференцируя по температуре, получим
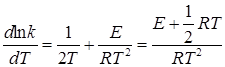 . (21.12)
. (21.12)
Сравнение последнего уравнения с уравнением Аррениуса (20.96) показывает, что опытная и истинная энергии активации связаны соотношением
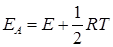 , (21.13)
, (21.13)
т.е. истинная энергия активации зависит от температуры, если считать E постоянной. Однако, поскольку величина 1/2 RT значительно меньше энергии активации, практически можно считать значения EA и E равными и не зависящими от температуры.
Совпадение уравнения Аррениуса с уравнением теории активных соударений позволяет вычислить предэкспоненциальный множительA в предположении, что A= Zo, или более точно Zo = AT1/2. Если принять для газокинетического диаметра величины порядка 10–8 см, то для обычных молекул при не слишком высоких температурах значение Zо 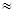 3 1014 см3 моль–1 с–1 = 3 1011 л моль–1 с–1
3 1014 см3 моль–1 с–1 = 3 1011 л моль–1 с–1
Реакции, для которых предэкспоненциальные множители близки к этой величине, называют “нормальными”. Наряду с ними существуют “быстрые” реакции со значениями Zо на 1 – 3 порядка больше. Объяснить их можно участием в процессе активации не только степеней свободы поступательного движения, но также колебательных и других видов движения. Появление быстрых реакций в растворах можно объяснить также каталитическим действием растворителя. В случае "медленных" реакций Zо значительно меньше (на 2 – 4 порядка) "нормального" значения 1014. Формально в этом случае теория вводит стерический факторP в выражение для константы скорости:
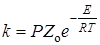 . (21.14)
. (21.14)
В некоторых случаях величина P достигает значений 10–3 – 10–4.
21.2. Мономолекулярные реакции
Мономолекулярная реакция представляет собою самопроизвольный распад единичных молекул, а ее скорость прямо пропорциональна давлению или концентрации в первой степени. Но согласно рассмотренному выше, активация молекул происходит путем столкновений, число которых пропорционально квадрату давления или концентрации. Схема, позволяющая понять механизм мономолекулярных реакций на основании представлений о соударениях молекул, предложена в 1922 г. Линдеманом.
Согласно схеме Линдеманареакция
А 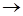 В + С
В + С
состоит из трех стадий:
1) образование возбужденной молекулы А* при столкновении двух нормальных молекул А:
А + А 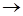 А*+ А k1
А*+ А k1
2) распад А* на продукты реакции:
А* 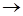 В + С k2
В + С k2
3) наряду с процессом активации (1) происходит дезактивация при соударениях:
А* + А 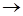 А + А k3
А + А k3
Процесс (2) распада активированной молекулы происходит через некоторый конечный промежуток времени после ее образования. Это время необходимо для перераспределения энергии внутри молекулы и сосредоточении ее на связи, подлежащей разрыву.
Если рассматривать молекулы А* как неустойчивый промежуточный продукт, к ним можно применить принцип стационарности (см. раздел 20.6):
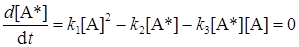 . (21.15)
. (21.15)
Концентрация [А*] отсюда равна:
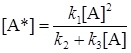 . (21.16)
. (21.16)
Общая скорость реакции определяется скоростью второй реакции:
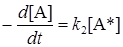 (21.17)
(21.17)
или с учетом (21.16)
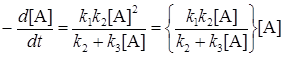 , (21.18)
, (21.18)
т.е. реакция имеет порядок, промежуточный между первым и вторым.
Как было сказано выше, активные молекулы А* имеют определенное время жизни t; сравнивая его со временем между столкновениями молекул t , можно рассмотреть два предельных случая.
При больших концентрациях (давлениях) столкновения происходят очень часто (t >> t) и большая часть молекул А* дезактивируется, не успев прореагировать, т.е. k3[А] >> k2 , и скорость реакции будет представлена уравнением реакции первого порядка:
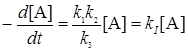 . (21.19)
. (21.19)
В случае малых давлений время между столкновениями молекул может значительно превысить время жизни активных молекул (t >>t), т.e. k2 >> k3[A]. Пренебрегая теперь в знаменателе уравнения (21.16) вторым слагаемым, получим кинетическое уравнение реакции второго порядка:
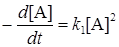 . (21.20)
. (21.20)
Скорость реакции в этом случае определяется скоростью процесса активации.
Таким образом, согласно схеме Линдемана, при уменьшении концентрации возможен переход от реакций первого порядка к реакциям второго порядка. Это заключение было подтверждено экспериментально для многих мономолекулярных реакций. Так, при термическом разложении изопропилхлорида константа скорости, рассчитанная по уравнению реакции первого порядка, остается постоянной при давлениях больше 0,5 кПа, а при более низких давлениях константа уменьшается и реакция не подчиняется этому кинетическому уравнению (рис.21.2, кривая 1). Введение в систему паров хлористого водорода при низких давлениях приводит к установлению постоянного значения константы (рис. 21.2, прямая 2). Аналогичное влияние оказывает введение водорода при разложении диэтилового эфира и изопропилового альдегида, введение азота при разложении нитрометана и т.д. Все эти явления можно объяснить участием и продуктов реакции и добавок в процессе активации (1) схемы Линдемана.
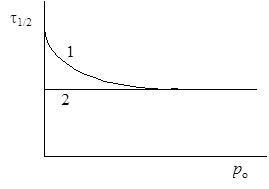 Рис.21.2. Зависимость периода полуреакции мономолекулярной реакции от давления: 1 – без добавок других газов, 2 – с добавками.
Рис.21.2. Зависимость периода полуреакции мономолекулярной реакции от давления: 1 – без добавок других газов, 2 – с добавками.
|
Несмотря на качественное соответствие схемы с экспериментальными наблюдениями, в целом она оказывается неудовлетворительной. Если исходить из схемы Линдемана, то между мономолекулярными и бимолекулярными реакциями нет принципиального различия. Если процесс активации происходит при столкновении двух молекул с относительной кинетической энергией вдоль линии центров, равной или большей E, то скорость мономолекулярной реакции не может превышать скорости активации, т.е. скорости бимолекулярного процесса. В отсутствии дезактивирующих соударений (3) схемы Линдемана теоретически возможная максимальная скорость реакции должна быть равна числу активирующих соударений (уравнение (21.4)):
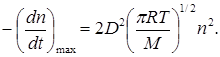 (21.21)
(21.21)
Согласно основному постулату химической кинетики скорость выражается уравнением реакции первого порядка:
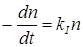 . (21.22)
. (21.22)
Из сравнения уравнений (21.21) и (21.22) определяем максимальную возможную константу скорости
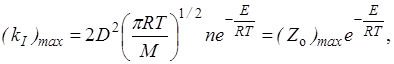 (21.19)
(21.19)
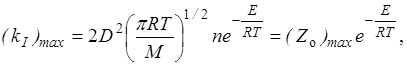 (21.23)
(21.23)
где Zo – частота столкновений одной молекулы:
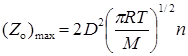 . (21.24)
. (21.24)
Экспериментальное значение Zoможно получить из уравнения Аррениуса, полагая (Zo)max 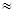 A. Сравнение этой величины с рассчитанной по уравнению (21.24) для многих реакций показывает, что экспериментальное значение Zов некоторых случаях на пять порядков выше “наибольшего” теоретического значения. Таким образом, если даже допустить, что все активные молекулы А реагируют, “максимальное” теоретическое значение Zо оказывается на 5 порядков меньше экспериментального.
A. Сравнение этой величины с рассчитанной по уравнению (21.24) для многих реакций показывает, что экспериментальное значение Zов некоторых случаях на пять порядков выше “наибольшего” теоретического значения. Таким образом, если даже допустить, что все активные молекулы А реагируют, “максимальное” теоретическое значение Zо оказывается на 5 порядков меньше экспериментального.
Путь усовершенствования теории столкновений для мономолекулярных реакций предложен Гиншельвудом, который первым обратил внимание на необходимость учета внутренних степеней свободы молекулы, подвергающейся распаду. Так как в мономолекулярных реакциях участвуют обычно сложные молекулы, в их активировании принимают участие не только степени свободы поступательного движения, но и другие виды, в первую очередь, степени свободы колебательного движения. По Гиншельвуду, молекула рассматривается как совокупность s осцилляторов с энергией e = nhn. Молекула становится способной к молекулярному распаду только в том случае, если на всех колебательных степенях свободы молекулы сосредоточится некоторая критическая энергия eо. Достижение суммарной энергии eо является необходимым и достаточным условием активации. Для определения скорости реакции необходимо вычислить долю молекул, у которых на s осцилляторах энергия имеет значение eо и больше.
Исходя из таких предпосылок, получены выражения для числа активных молекул nА* и скорости реакции при больших давлениях:
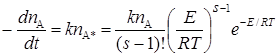 . (21.25)
. (21.25)
Последнее уравнение отличается от выражения, даваемого теорией столкновений, множителем (Е/RT)s–1/(s–1)!. Подбором соответствующих значений s можно согласовать теорию с опытом, однако теория не предсказывает и не объясняет необходимые величины s.
Можно полагать, что активными будут не все молекулы, обладающие энергией eо или большей, а только те из них, у которых избыток энергии сосредоточен на определенных связях. Это учитывается в теориях Касселя (1932 г.) и Слетера (1939 г.).
По Касселю, молекула представляет собою совокупность s гармонических осцилляторов с одинаковой частотой колебаний n, которые могут передавать друг другу энергию, кратную энергии кванта hn. Число осцилляторов принимается равным числу колебательных степеней свободы; для N-атомной нелинейной молекулы оно равно s = 3N – 6. Реагировать будет та молекула, у которой на одном определенном осцилляторе сосредоточено некоторое число квантов m. Для определения числа активных молекул необходимо найти вероятность такого распределения, при котором на одном из осцилляторов сосредоточено m квантов энергии, т.е. e = em = mhn, если молекула в целом обладает i квантами.
Согласно теории Касселя, предельное значение константы скорости мономолекулярной реакции (при больших давлениях) выражается уравнением:
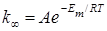 , (21.26)
, (21.26)
где энергия активации Em = Nm hn, а множитель A по смыслу представляет собою константу скорости перераспределения энергии от наиболее вероятного к такому, при котором один осциллятор обладает m квантами. При малых давлениях энергия активации становится равной
Еакт = Em – (s – 1)RT. (21.27)
Теория Касселя явилась значительным продвижением вперед по сравнению с простой теорией Гиншельвуда, однако и эта теория имеет существенные недостатки. Так, множитель A в основном уравнении (21.26) теоретически не определен, а совпадение расчетных значений с экспериментальными достигается только при подборе числа колебательных степеней свободы s.
В теории Слетерамолекула, состоящая из N атомов, рассматривается как совокупность классических и гармонических осцилляторов. Движение атомов в молекуле описывается изменением ряда внутренних координат (расстояние между атомами, угловые координаты); превращение молекулы происходит, когда соответствующая координата достигает критического значения. В отличие от других теорий, предполагается, что в невзаимодействующей молекуле частоты колебаний осцилляторов независимы, каждый атом в период между столкновениями сохраняет имеющийся у него запас колебательной энергии, которая может перераспределяться только в момент столкновения. Активной становится молекула, у которой на одной или нескольких координатах сосредоточивается энергия, равная или большая некоторой критической величины ea. В целом молекула, у которой i колебательных координат, имеет энергию Eакт = NSei . Предельная константа скорости при высоких давлениях равна
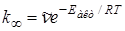 , (21.28)
, (21.28)
где 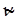 – средневзвешенная частота колебаний молекулы. Она характеризует колебательные движения молекулы в целом и вычисляется из частот нормальных колебаний молекулы n:
– средневзвешенная частота колебаний молекулы. Она характеризует колебательные движения молекулы в целом и вычисляется из частот нормальных колебаний молекулы n:
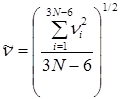 . (21.29)
. (21.29)
Очевидно, что 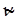 совпадает с множителем A уравнения (21.26) теории Касселя или уравнения Аррениуса, что дает возможность его расчета по данным о частотах колебаний атомов в молекуле. Для малых давлений теория Слетера дает переход к кинетическому уравнению реакции второго порядка и объясняет уменьшение энергии активации. Для некоторых реакций получено удовлетворительное согласие теории с экспериментальными результатами.
совпадает с множителем A уравнения (21.26) теории Касселя или уравнения Аррениуса, что дает возможность его расчета по данным о частотах колебаний атомов в молекуле. Для малых давлений теория Слетера дает переход к кинетическому уравнению реакции второго порядка и объясняет уменьшение энергии активации. Для некоторых реакций получено удовлетворительное согласие теории с экспериментальными результатами.
21.3. Теория активированного комплекса
(переходного состояния)
В основе теории лежит представление о том, что в ходе химической реакции начальная конфигурация атомов в реагирующих молекулах переходит в конечную путем непрерывного изменения межатомных расстояний.
Рассмотрим простой случай реакции между атомом А и двухатомной молекулой ВС:
А + ВС ® АВ + С
Реакция проходит с наименьшей затратой энергии, если атомы расположены на одной линии, а ход реакции можно описать, используя два межатомных расстояния r1 и r2:
А + В–C ® А ------- В --------- C ® А–В + C
| r1 ®| r2 | | 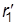 ®|
®| 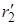 ®| |
®| | 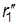 |
| 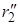 ®|
®|
В процессе реакции расстояние r1 уменьшается, а r2 увеличивается, при этом образуется промежуточная конфигурация А---В---С, в которой связь В–С ослаблена, но окончательно не разорвана, а связь А–В начала образовываться. Такая конфигурация и получила название переходного состояния (Поляни и Эванс), или активированного комплекса (Эйринг, 1935). Активированный комплекс мгновенно разлагается, поэтому нельзя считать, что это хотя и неустойчивая, но все же в принципе доступная для выделения промежуточная форма. В теории постулируется, что активированный комплекс всегда превращается в конечные вещества, т.е. атомы, достигнув конфигурации активированного комплекса, продолжают двигаться по инерции в направлении образования продуктов реакции.
21.3.1. Поверхность потенциальной энергии
При изменении межатомных расстояний изменяется и потенциальная энергия системы U. В принципе возможен полный теоретический расчет функции U = f(r1, r2), однако ввиду очень больших трудностей, применяются полуэмпирические методы с использованием аппарата статистической механики. Вычисленные значения U можно представить в виде поверхности потенциальной энергии (рис. 21.3). Построение таких диаграмм сложно и обычно пользуются изображениями проекций изоэнергетических сечений на плоскость r1 – r2 (рис. 21.4). Каждая линия на графике отвечает определенному уровню энергии в зависимости от межатомных расстояний, числа показывают условные величины этих энергий.
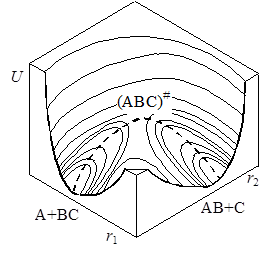 Рис. 21.3. Поверхность потенциальной энергии
Рис. 21.3. Поверхность потенциальной энергии
|
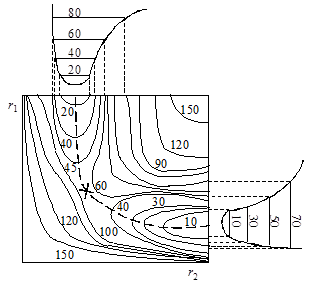 Рис.21.4. Проекция поверхности потенциальной энергии
Рис.21.4. Проекция поверхности потенциальной энергии
|
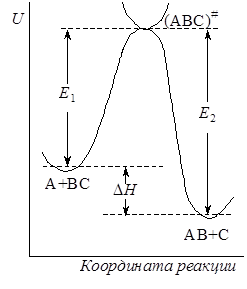 Рис. 21.5. Энергетический профиль пути реакции
Рис. 21.5. Энергетический профиль пути реакции
|
На поверхности можно отметить две “долины” (“ложбины”), сечения которых представлены на рис. 21.4 сверху и справа, разделенные “перевалом” (“седловиной”). Верхняя левая часть диаграммы соответствует исходному состоянию системы (большие r1 и малые r2), нижняя правая – продуктам реакции (малые r1, большие r2). Переход системы из начального в конечное состояние возможен различными путями, но наиболее вероятным будет переход с наименьшей затратой энергии. Таким будет прохождение системы по дну одной “долины” через перевальную точку и по дну другой “долины”. Такая совокупность наиболее вероятных состояний системы называется путем реакции, или координатой реакции. На рис. 21.3 и 21.4 путь реакции изображен пунктиром, отмеченная крестиком высшая точка этого пути соответствует образованию активированного комплекса.
Если разрезать поверхность потенциальной энергии вдоль пути реакции перпендикулярно плоскости r1 – r2 и развернуть поверхность сечения в одну плоскость, то получим кривую сечения, имеющую максимум, которую называют профилем пути реакции(рис. 21.5). Точка максимума, как говорилось выше, отвечает переходному состоянию А--В--С, а высота E представляет энергию активации – разность между потенциальной энергией активированного комплекса и начальных продуктов, т.е. ту энергию, которой должны обладать частицы, чтобы преодолеть потенциальный барьер и образовать продукты реакции.
Для обратной реакции АВ + С ® А + ВС конфигурация активированного комплекса та же, что и для прямой, но путь реакции проходит в противоположном направлении с энергией активации E2. Разность энергий активации прямой и обратной реакции представляет собой тепловой эффект реакции:
DE = E2 – E1 = DH
21.3.2. Основное уравнение теории активированного комплекса
При выводе основного уравнения предполагается, что протекание реакции не нарушает распределения молекул по состояниям и можно использовать статистически равновесное распределение Максвелла–Больцмана.
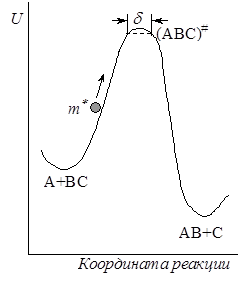 Рис. 21.6.Схема движения частицы по поверхности потенциальной энергии
Рис. 21.6.Схема движения частицы по поверхности потенциальной энергии
|
Движение ядер атомов происходит значительно медленнее, чем движение электронов, поэтому при любой конфигурации ядер электроны успевают перестраиваться. В связи с этим элементарный акт реакции считается протекающим адиабатно, т.е. движение ядер и электронов происходит независимо и потенциальная энергия ядер при движении изменяется непрерывно.
Предположение об адиабатности процесса позволяет прибегнуть к механической аналогии, представив ход реакции как движение некоторой частицы с эффективной массой m* по поверхности потенциальной энергии (рис. 21.6). Если частица обладает достаточной кинетической энергией, то она может достичь перевальной точки и затем скатиться с возрастающей скоростью на другую сторону барьера. Для реакции А + ВС это значит, что относительная кинетическая энергия при сближении частиц достаточна, чтобы преодолеть силы отталкивания и образовать активированный комплекс, который распадается на продукты реакции.
С этой точки зрения скорость протекания элементарного процесса определяется скоростью, с которой частица m* пересекает вершину потенциального барьера, которую можно выразить какой-то средней величиной. Для упрощения расчетов вершина перевала представляется в виде плоского участка пути реакции длиною d. Это соответствует допущению, что переходное состояние существует не в одной точке с фиксированными координатами r1 и r2 , а в некотором интервале этих расстояний. Движение частицы m* на плоском участке d можно считать одномерным, а ее средняя скорость 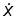 тогда будет равна скорости теплового движения молекулы с массой m* вдоль одной координаты:
тогда будет равна скорости теплового движения молекулы с массой m* вдоль одной координаты:
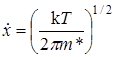 . (21.30)
. (21.30)
Средняя продолжительность жизни активированного комплекса t равна тогда
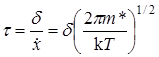 . (21.31)
. (21.31)
Концентрация активированных комплексов c# на интервале d равна числу возникающих активированных комплексов или числу элементарных актов реакции за время t, а скорость реакции – числу элементарных актов за единицу времени:
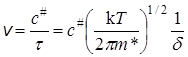 . (21.32)
. (21.32)
Согласно основному постулату химической кинетики скорость бимолекулярной реакции
А + В ® (АВ)# ® С + D
равна
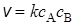 . (21.33)
. (21.33)
Сравнивая два последних уравнения, получим выражение для константы скорости реакции:
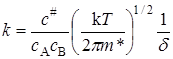 . (21.34)
. (21.34)
Согласно теории, к реагирующей системе применима статистика Максвелла – Больцмана, поэтому константа скорости элементарной реакции А + В ® С + D, протекающей в отсутствии равновесия, мало отличается от константы скорости, вычисленной в предположении существования химического равновесия как с конечными продуктами, так и с промежуточными активными комплексами. При этих условиях уравнение реакции можно представить в виде А + В L (АВ)# ® С + D, а выражение (21.34) для константы скорости записать через концентрации, соответствующие равновесному состоянию:
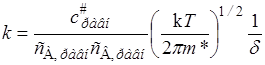 . (21.35)
. (21.35)
Отношение равновесных концентраций заменим константой равновесия
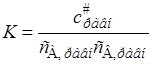 . (21.36)
. (21.36)
Величина K вычисляется методами статистической механики, которые дают возможность выразить константу равновесия через статистические суммы по состоянию Q на единицу объема (см. гл. 14):
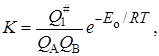 (21.37)
(21.37)
где Eo – энергия активации при абсолютном нуле температуры.
Суммы по состояниям исходных веществ QA и QB обычно определяются на основании молекулярных характеристик. Сумму по состояниям активированного комплекса 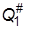 разбивают на два сомножителя, один из которых соответствует одномерному поступательному движению частицы m* через вершину перевала. Статистическая сумма поступательного движения в трехмерном пространстве объема V равна
разбивают на два сомножителя, один из которых соответствует одномерному поступательному движению частицы m* через вершину перевала. Статистическая сумма поступательного движения в трехмерном пространстве объема V равна
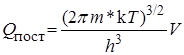 . (21.38)
. (21.38)
Для определения Qпост для одной степени свободы надо извлечь из этого выражения кубический корень, причем в нашем случае V3/2 будет соответствовать пути реакции d:
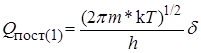 , (21.39)
, (21.39)
и
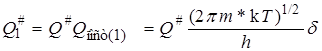 , (21.40)
, (21.40)
где Q# – сумма по состояниям активированного комплекса для всех остальных видов энергии, т.е. двух степеней свободы поступательного движения в обычном пространстве, электронной, колебательной, вращательной энергий.
Подставляя уравнение (21.40) в (21.37), получаем
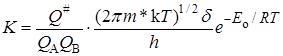 . (21.41)
. (21.41)
Введем обозначение
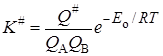 . (21.42)
. (21.42)
K# можно условно назвать константой равновесия между исходными веществами и активированным комплексом, хотя в действительности такого равновесия нет. Тогда константа скорости
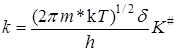 . (21.43)
. (21.43)
Подставляя уравнение (21.43) в (21.34) с учетом выражений (21.36) и (21.35), получим основное уравнение теории активированного комплексадля константы скорости реакции:
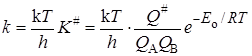 . (21.44)
. (21.44)
Это уравнение получено в предположении адиабатного протекания процесса. При неадиабатных процессах существует возможность “скатывания” частицы с вершины барьера в долину исходных веществ. Эта возможность учитывается введением трансмиссионного коэффициента(коэффициента прохождения) c и в общем случае константа скорости определяется выражением:
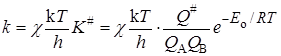 . (21.45)
. (21.45)
Очевидно, что c равен или меньше единицы, но путей его теоретического расчета нет.
21.3.3. Свободная энергия активации
Константа равновесия реакции, протекающей при постоянном давлении, связана с изменением изобарно-изотермического потенциала (энергии Гиббса) уравнением (11.20). В том случае, когда реагирующие вещества находятся в стандартном состоянии, для реакции образования активного комплекса можно записать:
DG# = –RTlnK#, (21.46)
где DG# – изменение энергии Гиббса при переходе системы из исходного состояния в активное.
Так как по уравнению Гиббса – Гельмгольца
DG# = DН# – ТDS#, (21.47)
то для константы равновесия получим:
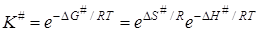 , (21.48)
, (21.48)
а константа скорости реакции (уравнение (21.45)) будет равна
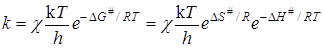 , (21.49)
, (21.49)
где DH# и DS# представляют собой теплоту и энтропию активации.
Уравнение (21.49) показывает, что скорость реакции определяется не теплотой активации, а изменением энергии Гиббса активации DG# (или DF# для реакций при постоянном объеме), т.е. существенное влияние на скорость реакции может оказывать изменение энтропии DS#, увеличение которой способствует повышению скорости.
Сравнение уравнения (21.49) с уравнением Аррениуса (20.98) или уравнением теории соударений (21.14) указывает на их сходство, если положить, что теплота активации DH# соответствует энергии активации E. Связь между ними можно установить следующим образом. Прологарифмируем уравнение (21.44):
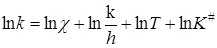 . (21.50)
. (21.50)
Дифференцирование его по температуре и сравнение с уравнением Аррениуса дает:
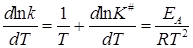 . (21.51)
. (21.51)
Зависимость K# от температуры определяется изобарой Вант-Гоффа (11.26)
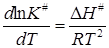 . (21.52)
. (21.52)
Таким образом, мы получаем
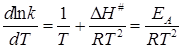 , (21.53)
, (21.53)
откуда следует связь между экспериментальной энергией активации EA и теплотой активации:
EA = DН# + RT. (21.54)
При умеренных температурах RT << DH# и практически можно считать, что EA = DH#.
21.3.4. Сравнение теорий активных столкновений и переходного состояния
При реакции между двумя атомами А и В константа равновесия при образовании активированного комплекса АВ# равна:
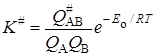 . (21.55)
. (21.55)
Статистические суммы по состояниям атомов с массой mi, которые имеют три степени свободы поступательного движения, равны:
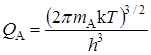 ,
, 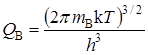 . (21.56)
. (21.56)
Активированный комплекс, образованный из двух атомов, кроме трех поступательных, имеет две вращательные степени свободы и для него
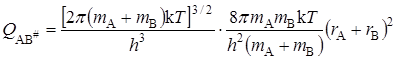 . (21.57)
. (21.57)
Тогда по уравнению (21.45) константа скорости будет равна (если положить c = 1):
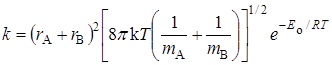 , (21.58)
, (21.58)
что совпадает с уравнением теории активных соударений (21.8).
При реакции между многоатомными молекулами, которые имеют поступательные, вращательные и колебательные степени свободы со статистической суммой по состояниям qi на одну степень свободы, теория активированного комплекса дает в уравнении (21.58) дополнительный множитель (qкол/qвращ)5, который аналогичен стерическому фактору теории соударений и называется иногда вероятностным фактором.
21.4. Реакции в растворах
| |
Первые систематические исследования влияния растворителя на скорость реакций были проведены в конце ХIХ века Н.А.Меншуткиным. Он открыл новый класс реакций образования четвертичных аммониевых солей из алкилгалогенидов RГ и третичных аминов R3N:
RГ + R3N ® R NГ
Особенностью этих реакций является их чрезвычайно малая скорость, чему соответствует малое значение предэкспоненциальных множителей A в уравнении Аррениуса – величины A имеют порядок 102 –104 вместо "нормального" значения 3.1011 л. моль-1.с-1, а значения стерического множителя P имеют порядок 10-8 – 10-10. В таблице 21.1 приведены кинетические характеристики для некоторых из этих реакций.
Предложены различные объяснения малой скорости реакций Меншуткина. Одной из причин может быть необходимость определенной ориентации молекул в момент столкновения; кроме того, реакция может проходить при столкновении активированных молекул, в которых осуществляется подходящее распределение энергии по внутренним степеням свободы, например, когда один из колеблющихся атомов наиболее отклонился от нормального положения. Различная сольватация растворителем исходных веществ и активированного комплекса влияет на энергию активации, что также сказывается на константе скорости.
Таблица 21.1
Кинетические характеристики некоторых реакций Меншуткина
| Реакция | Растворитель | A л.моль-1с-1 | E кДж/моль | P |
| (C2H5)3N + C2H5Br | C6H6 CH3COCH3 | 2,8.102 8,5.103 | 42,8 49,0 | 5,3.10–10 1,6.10–8 |
| C6H5(CH3)2N + CH3I | C6H5NO2 C2H2Cl4 | 2,6.104 2,1.104 | 54,5 48,9 | 5,3.10–8 4,8.10–8 |
| C6H5(CH3)2N + C2H5 | CH3COCH3 | 2,7.104 | 57,2 | 6,3.10–8 |
С другой стороны, можно привести некоторые примеры реакций, скорости которых мало отличаются в газовой фазе и растворе. В таблице 21.2 приведены относительные константы скорости и энергии активации реакции распада оксида азота N2O5 в различных растворителях.
Некоторые важные выводы о кинетике реакций в растворах можно получить, используя теорию активированного комплекса.
Для реакции
А + В ® АВ# ® продукты
константа скорости равна
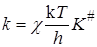 . (21.59)
. (21.59)
Если реакция протекает при достаточно низких давлениях в газовой  фазе и разбавленных растворах , то
фазе и разбавленных растворах , то

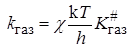 , (21.60)
, (21.60)
откуда отношение констант скоростей будет равно
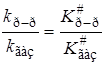 . (21.61)
. (21.61)
Таблица 21.2
Кинетические характеристики реакции распада N2O5
| Растворитель | 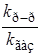
| E кДж/моль |
| Газовая фаза | 1,00 | 102,5 |
| CH3NO2 | 0,81 | 102,5 |
| Br2 | 1,14 | 100,4 |
| CHCl2CCl3 | 1,16 | 104,6 |
| CCl4 | 1,24 | 100,8 |
| CH2ClCH2Cl | 1,26 | 102,1 |
| CHCl3 | 1,45 | 102,9 |
Константа равновесия образования активированного комплекса выражается через концентрации c реагирующих веществ:
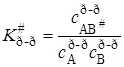 . (21.62)
. (21.62)
Для газов 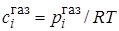 ,
,  где pi – парциальное давление i-го компонента в газовой фазе. По закону Рауля pi = poixi , а для разбавленных растворов выполняется примерное равенство
где pi – парциальное давление i-го компонента в газовой фазе. По закону Рауля pi = poixi , а для разбавленных растворов выполняется примерное равенство 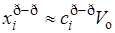 , где Vo – молярный объем чистого растворителя; таким образом
, где Vo – молярный объем чистого растворителя; таким образом
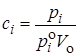 . (21.63)
. (21.63)
Подставляя концентрации веществ А, В, АВ# в уравнение (21.62), а затем в (21.61), получим для реакции n-го порядка
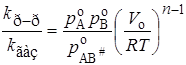 . (21.64)
. (21.64)
Это уравнение получено Бенсоном. Если предположить, что молярные объемы растворителя и растворенных веществ примерно равны, молярный объем АВ# равен сумме молярных объемов А и В, а также ввести некоторые дополнительные упрощения, то получим соотношение
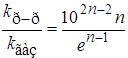 . (21.65)
. (21.65)
Это означает, что для реакций первого порядка (n = 1) константы скорости реакции в газовой фазе и растворе должны быть одинаковы, если механизм и энергии активации в двух фазах не отличаются. Для бимолекулярной реакции
kp-p/kгаз » 75, т.е. реакция в растворе должна протекать быстрее, чем в газовой фазе.
В случае неидеальных растворов константа равновесия должна выражаться не через концентрации, а через активности ai = cifi (fi – коэффициент активности):
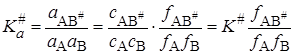 . (21.66)
. (21.66)
Подставляя значение K# в уравнение (21.45), получим
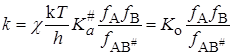 . (21.67)
. (21.67)
Уравнение (21.67), полученное Бренстедом (1922) и Бьеррумом(1924), позволяет объяснить влияние на скорость таких факторов как диэлектрическая проницаемость среды, заряд реагирующих частиц, концентрация добавляемых электролитов и т.п.
Если реагируют нейтральные частицы, то для определения коэффициентов активности можно воспользоваться уравнением Ленгмюра:
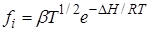 , (21.68)
, (21.68)
где b – постоянная, DH – теплота испарения веществ. В этом случае
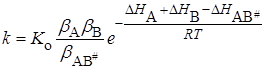 . (21.69)
. (21.69)
Если в растворе нет сильного межмолекулярного взаимодействия между растворителем и реагирующими веществами А, В, АВ#, то показатель степени мало отличается при протекании реакции в газовой фазе и в растворе, а изменение константы скорости будет определяться предэкспоненциальным множителем, зависящим от bA , bB , 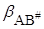 . Взаимодействие растворителя с реагентами – сольватация – приводит к увеличению или уменьшению скорости реакции.
. Взаимодействие растворителя с реагентами – сольватация – приводит к увеличению или уменьшению скорости реакции.
При реакциях между ионами проявляется сильное электростатическое взаимодействие, зависящее от диэлектрической проницаемости среды e. Для оценки влияния e на кинетику ионных реакций используем уравнение теории активированного комплекса:
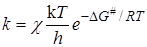 (21.70)
(21.70)
и представим энергию активации DG# в виде двух составляющих, которые соответствуют неэлектростатическому и электростатическому взаимодействиям:
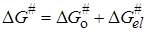 . (21.71)
. (21.71)
Изменение энергии Гиббса при переносе иона из вакуума в среду с диэлектрической проницаемостью e можно представить по Борну (см. разд. 15.2) как сумму слагаемых: 1) изменение энергии при разряде иона в вакууме, равное -ziei/2ri (zi и ri – заряд и радиус иона); 2) изменение энергии при переносе незаряженной частицы в бесконечно разбавленный раствор; 3) изменение энергии при заряжении иона, равное zi2ei2 /2rie. Второе слагаемое можно включить в неэлектростатическую составляющую 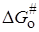 , а изменение энергии при электростатическом взаимодействии будет равно в расчете на один моль
, а изменение энергии при электростатическом взаимодействии будет равно в расчете на один моль
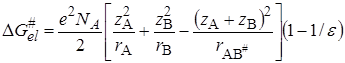 . (21.72)
. (21.72)
Подстановка уравнения (21.71) в (21.70) и логарифмирование дает
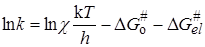 . (21.73)
. (21.73)
Обозначив первые два члена справа как lnko и подставив значения 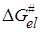 из уравнения (21.72), получим:
из уравнения (21.72), получим:
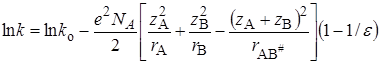 . (21.74)
. (21.74)
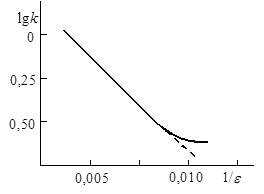 Рис. 21.7. Зависимость lnk от обратной диэлектрической проницаемости растворителя
Рис. 21.7. Зависимость lnk от обратной диэлектрической проницаемости растворителя
|
Отсюда следует, что если радиусы частиц остаются неизменными в различных растворителях, то логарифм константы скорости является линейной функцией обратной диэлектрической проницаемости растворителя. Например, линейная зависимость выполняется в достаточно широком интервале диэлектрических проницаемостей для реакции между ионами тетрабромсульфофталеина (БСФ) и ионами гидроксила в смесях вода – метанол, вода – этанол при 298 К (рис. 21.7). Отклонения от линейности связаны, видимо, с тем, что кроме электростатического взаимодействия на кинетику оказывают влияние и другие факторы, обусловленные неэлектростатическими взаимодействиями, избирательной сольватацией и т.д.
При реакции между ионами коэффициенты активности в уравнении (21.67) можно представить на основании теории растворов сильных электролитов Дебая – Гюккеля (раздел 15.5):
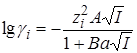 . (21.75)
. (21.75)
Представив уравнение (21.67) в логарифмической форме и выразив коэффициенты активности по уравнению Дебая – Гюккеля(заряд активированного комплекса 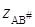 = zA + zB), получим для логарифма константы скорости ионной реакции:
= zA + zB), получим для логарифма константы скорости ионной реакции:
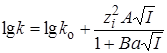 . (21.76)
. (21.76)
Для очень разбавленных растворов с малой ионной силой можно использовать первое приближение теории Дебая – Гюккеля 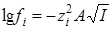 , в этом случае
, в этом случае
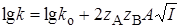 , (21.77)
, (21.77)
т.е. логарифм константы скорости является линейной функцией от корня из ионной силы.
Влияние ионной силы на константу скорости реакции вследствие изменения активности реагентов называется первичным солевым эффектом. Скорость реакции может меняться также за счет уменьшения эффективной концентрации ионного реагента, образующегося при диссоциации слабого электролита, при добавках соли. Это вторичный солевой эффект. Например, каталитическое действие уксусной кислоты на инверсию сахарозы уменьшается в присутствии ацетатов щелочных металлов, так как в этом случае сильно понижается эффективная концентрация ионов водорода.
Совокупность явлений, связанных с солевым эффектом, показывает, что изменение среды, в которой протекает реакция, влияет на ее скорость так же, как и на равновесие между реагентами. И для констант скоростей и для констант равновесий выполняется один и тот же предельный закон, а отклонения от него, связанные со специфическими взаимодействиями, проявляются в одних и тех же условиях и имеют одинаковый характер. Аналогичное влияние на скорость и равновесие подтверждает справедливость общей теории переходного состояния. Существование солевого эффекта показывает, что влияние свойств среды на скорость реакции определяется разностью стандартных потенциалов реагирующих веществ и активированного комплекса, причем влияние на активированный комплекс в принципе не отличается от влияния на стабильную молекулу.
В связи с этим было предложено ряд корреляционных уравнений, основанных на так называемом принципе линейных соотношений свободной энергии. Согласно этому принципу, если молекулу представить как совокупность реагирующей группы X и нереагирующего остатка R, между которыми отсутствуют сильные специфические взаимодействия, то:
1) для любой реакции, затрагивающей X, изменение DG# , вызываемые изменениями в R, линейно связаны с изменениями DGo в той же реакции;
2) изменения DG# или DGo , вызываемые изменениями в R, для одной реакции с участием группы X1 , линейно связаны с соответствующими величинами для другой реакции с участием X1 и для реакции с участием другой группы X2.
Принцип линейной зависимости свободных энергий можно представить уравнениями:
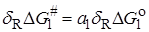 , (21.78)
, (21.78)
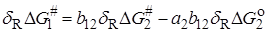 , (21.79)
, (21.79)
где dR – оператор Леффлера – Грюнвальда, отражающий влияние изменения строения на какую-либо зависящую от него величину: 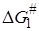 и
и 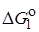 относятся к реакции 1, а
относятся к реакции 1, а 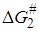 и
и 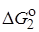 – к реакции 2. Величины a1, a2,b12 не зависят от R, но зависят от рассматриваемых реакций.
– к реакции 2. Величины a1, a2,b12 не зависят от R, но зависят от рассматриваемых реакций.
Наиболее изученной областью применения уравнения (21.78) является зависимость, полученная Бренстедом, для скорости реакций, катализируемых кислотами или основаниями:
dRlgk =adRlgK. (21.80)
Она связывает константу скорости k данной каталитической реакции, катализируемой рядом кислот или оснований, с константами равновесия K, характеризующими силу кислоты или основания. Параметр a характеризует каталитическую реакцию и не зависит от катализатора.
Гаммет предложил уравнение, которое учитывает влияние заместителя на константу скорости или равновесия в какой-либо реакции, характерной для данного класса ароматических соединений. Уравнение Гамметазаписывается в виде
lgk = lgko + rs, (21.81)
где k и ko – константы скорости реакции замещенного и незамещенного ароматического соединения рассматриваемого класса, s - константа, характеризующая заместитель, r - реакционная константа, зависящая от реакции, среды и температуры.
Так как из экспериментальных данных можно получить лишь величину произведения rs, то необходимо приписать некоторое исходное значение каким-либо r и s. Гаммет принял r = 1 для равновесия ионизации замещенных бензойных кислот. Тогда заместитель i можно характеризовать константой s, определяемой из соотношения
s = lgki – lgko, (21.82)
где ko – константа ионизации бензойной кислоты, а ki – константа ионизации замещенной бензойной кислоты. Беря эти значения s, можно получить величину r для других реакций, а из этого, в свою очередь, могут быть вычислены s для заместителей, эффект которых на силу бензойных кислот ранее не был определен.
Уравнение Гаммета мало применимо к алифатическим соединениям, а также к реакциям с участием молекул с заместителями в орто-положении, когда возникают стерические затруднения.
| <== предыдущая лекция | | | следующая лекция ==> |
| Предмет химической кинетики | | | Волноводы и резонаторы |
Дата добавления: 2015-12-16; просмотров: 6416;
