Предмет химической кинетики

Термодинамика позволяет с большой точностью предсказать принципиальную возможность протекания процесса и конечное состояние системы, однако она не дает никаких сведений о способах фактической реализации процесса и времени его протекания. В действительности же некоторые процессы протекают настолько быстро, что представляются мгновенными, другие идут настолько медленно, что практически какие-либо изменения в системе не наблюдаются. Не существует какой-либо связи между величиной химического сродства и скоростью реакции. Реакции между веществами с большим химическим сродством могут протекать медленно, и наоборот, вещества с малым химическим сродством могут реагировать очень быстро. Так, согласно термодинамике, смесь газообразных водорода и кислорода при обычной температуре должна практически полностью превращаться в воду (для этой реакции DG^o = –450 кДж), однако в эксперименте образование воды практически не наблюдается. Химический потенциал алмаза в обычных условиях больше химического потенциала графита и, следовательно, алмаз должен самопроизвольно превращаться в графит, в действительности же такое превращение не происходит.

Такое кажущееся противоречие между теоретическими предсказаниями и практическими результатами обусловлено тем, что в термодинамике учитывается только начальное и конечное состояния системы, но не рассматривается механизм перехода и не фигурирует такой практически важный фактор как время. Реально всякое превращение связано с преодолением некоторого энергетического барьера – разрыв связей в молекулах реагирующих веществ, перестройка структуры кристаллической решетки и т.д. Если энергетический барьер высок, то теоретически возможная реакция протекает настолько медленно, что за практически ограниченный промежуток времени каких-либо изменений не наблюдается (реакция “не идет”).

Таким образом, кроме термодинамического подхода, громадное значение приобретает и другой аспект исследования химических реакций – изучение их с точки зрения скоростей. Исследование закономерностей протекания процессов во времени и является предметом химической кинетики.

Можно выделить две главные задачи химической кинетики, определяющие ее практическое и теоретическое значение: 1) экспериментальное исследование скорости реакций и ее зависимость от условий протекания (концентрации реагирующих веществ, температуры, присутствия других веществ и т.д.) и 2) установление механизма реакции, т.е. числа элементарных стадий и состава образующихся промежуточных продуктов.

Строгое теоретическое рассмотрение кинетических параметров в настоящее время возможно лишь для простейших реакций в газовой фазе. Весьма ценные сведения о течении реакций дает эмпирический макроскопический подход. Количественное описание скорости реакции в зависимости от концентрации реагирующих веществ базируется на основном постулате химической кинетики и составляет предмет формальной кинетики.

20.2. Основные понятия и определения

Скоростью реакцииназывают количество молекул вещества, реагирующих в единицу времени. Сравнение скоростей различных реакций возможно лишь в случае, когда объемы реагирующих систем одинаковы, поэтому скорость v относят к единице объема:

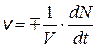, (20.1)

где V – объем системы, dN – число молекул вещества, прореагировавших за время dt. Знак плюс относится к случаю, когда скорость определяется по образующемуся в реакции веществу, знак минус – когда скорость определяется по исходному веществу. Так как в химической реакции вещества реагируют в строго определенных соотношениях, то скорость можно рассчитать по любому веществу, участвующему в реакции.

Если объем системы остается неизменным, то можно вместо числа частиц использовать концентрацию (c = N/N_AV, где N_A – число Авогадро) и тогда скорость реакции равна изменению концентрации в единицу времени:

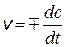. (20.2)

Так как в ходе реакции концентрации веществ изменяются, скорость является функцией времени. Можно ввести понятие средней скорости реакции 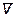в заданном интервале времени от t₁ до t₂:

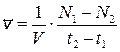, (20.3)

где N₁ и N₂ – число молекул вещества в моменты времени t₁ и t₂.

При уменьшении временного интервала, когда (t₂ – t₁) ® 0, приходим к выражению (20.1, 20.2) для истинной скорости.

В общем случае скорость реакции зависит от многих факторов: природы реагирующих веществ, природы растворителя для реакций в растворах, концентрации, температуры, присутствия других веществ (катализаторов, ингибиторов) и т.п. Для данной реакции при постоянных условиях ее протекания скорость в каждый момент зависит от концентрации. Эта зависимость выражается основным постулатом химической кинетики:

В каждый момент времени скорость химической реакции пропорциональна произведению концентраций реагирующих веществ, возведенных в некоторые степени.

Так, для некоторой реакции между веществами A, B, D,...

aA + bB + dD + ... ® продукты

скорость

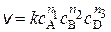... (20.4)

Показатели степеней n₁, n₂, n₃,… называются порядком реакциипо веществам A, B, D,… а их суммарное значение n = n₁ + n₂ + n₃ + ... называется общим порядком реакции.

Коэффициент пропорциональности k в кинетическом уравнении (20.3) называется константой скорости, или удельной скоростью реакции. Величина k численно равна скорости реакции, когда концентрации всех реагирующих веществ равны единице: c_A = c_B = c_D = 1. Константы скорости различны для разных реакций и зависят от температуры.

Во многих случаях порядок не совпадает со стехиометрическими коэффициентами в уравнении реакции (т.е. n₁ ¹ a, n₂ ¹ b и т.д.).

Так, например, для двух подобных реакций с одинаковыми стехиометрическими уравнениями, получены совершенно различные кинетические уравнения:

для реакции H₂ + I₂ = 2HI

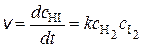, (20.5)

а для реакции H₂ + Br₂ = 2HBr

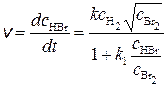. (20.6)

Это связано с различиями в механизмах протекания реакций. Большинство реакций протекает в несколько стадий, имеющих различные скорости, поэтому стехиометрическое уравнение представляет собой суммарный результат всех элементарных стадий, а общая скорость реакции определяется скоростью наиболее медленной стадии (лимитирующей реакции).

В связи с этим для элементарных реакций вводится понятие молекулярность– число молекул, принимающих участие в элементарном акте химического взаимодействия. Если в элементарном акте участвует одна молекула (например, происходит распад молекулы), реакция является мономолекулярной. Если в элементарном акте взаимодействуют две молекулы, реакция называется бимолекулярной, например, приведенные выше реакции водорода с бромом или йодом. В тримолекулярных реакциях принимают участие три частицы, как например, в реакции рекомбинации атомов водорода в молекулу:

Н + Н + М = Н₂ + М,

где М – молекула водорода или любая другая частица.

В отличие от молекулярности порядок реакции может быть нулевым, целочисленным или дробным. Лишь для элементарных реакций численные значения молекулярности и кинетического порядка совпадают. Моно-, би- и тримолекулярные реакции являются в то же время реакциями первого, второго и третьего порядка, однако обратное заключение может оказаться ошибочным. Например, реакция разложения паров дихлорэтана

CH₂Cl–CH₂Cl 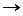CHCl=CH₂ + HCl

является реакцией первого порядка, ее скорость пропорциональна концентрации дихлорэтана:

.

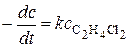Но эту реакцию нельзя назвать мономолекулярной, так как изучение ее механизма показало, что реакция протекает через несколько элементарных стадий, моно- и бимолекулярных. В таком случае вообще нельзя говорить о молекулярности реакции в целом, можно лишь указать на экспериментально установленный первый порядок.

В некоторых случаях концентрации одного или нескольких из реагирующих веществ в ходе реакции меняются очень мало и их можно считать постоянными. Тогда концентрации этих веществ можно включить в константу скорости уравнения (20.4) и кажущийся порядок реакции уменьшается, реакция становится псевдо n-ого порядка, где n – сумма показателей степеней при изменяющихся концентрациях.

Так, для реакции инверсии тростникового сахара, которая катализируется ионами водорода

С₁₂Н₂₂О₁₁ + Н₂О 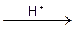2С₆Н₁₂О₆,

кинетическое уравнение можно записать в виде:

,

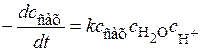т.е. это реакция третьего порядка. Но концентрация ионов водорода не меняется в ходе реакции, а концентрация воды, если она взята в большом избытке, также практически не изменяется. Таким образом, изменяется только концентрация сахара, и тогда кинетическое уравнение можно записать как

,

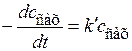т.е. это реакция псевдопервого порядка.

20.3. Простые необратимые реакции

В системе одновременно и независимо могут протекать реакции с различной скоростью, но в противоположных направлениях. Через некоторое время после начала скорости прямой и обратной реакций становятся одинаковыми, и система достигает состояния равновесия. Такие реакции называются кинетически обратимыми. Это понятие следует отличать от обратимости процесса в термодинамическом смысле. Термодинамически обратимый процесс характеризуется тем, что в нем скорости прямого и обратного процессов различаются на бесконечно малую величину, а в любой момент времени состояние системы бесконечно мало отличается от равновесного. Таким образом, понятия кинетической и термодинамической обратимости совпадают лишь вблизи к состоянию химического равновесия, поэтому кинетически обратимые реакции более точно следовало бы называть двусторонними.

В принципе все химические реакции являются двусторонними, в действительности же некоторые из них в определенных условиях протекают лишь в одном направлении до практически полного исчезновения исходных веществ, т.е. равновесие в таких случаях очень сильно смещено в сторону образования продуктов. Такие реакции называются кинетически необратимыми, или односторонними.

20.3.1. Односторонние реакции первого порядка

К реакциям первого порядка относятся в основном реакции разложения, например, реакция разложения оксида азота

N₂O₅ 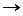2NO₂ + O₂

или диэтилового эфира

CH₃OCH₃ 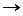CH₄ + H₂ + CO

В общем случае запишем уравнение реакции первого порядка в виде

A ® продукты

Если в начальный момент времени (t = 0) концентрация вещества А равнялась a, а через некоторое время она уменьшилась на x, то скорость реакции в любой момент времени, согласно уравнениям (20.3) и (20.4) равна

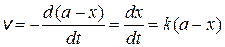. (20.7)

Разделим переменные и проинтегрируем полученное уравнение, учитывая, что в начальный момент времени x = 0:

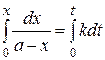. (20.8)

В результате получим кинетическое уравнение реакции первого порядка:

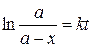(20.9)

или

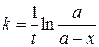. (20.10)

Из последнего уравнения видно, что размерность константы скорости соответствует обратному времени (t^–1) и в зависимости от величин скорости ее можно выражать в c^–1 , мин^–1, ч^–1 и т.д. Так как концентрации вещества входят в уравнение в виде отношения, то их можно выражать в любых единицах, а численные значения константы скорости от этого не зависят.

Потенцируя уравнение (20.9), получим значения концентраций реагирующего вещества в любой момент времени:

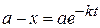(20.11)

или для концентрации прореагировавшего вещества к моменту t

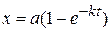, (20.12)

откуда следует экспоненциальный характер изменения концентрации реагирующего вещества во времени (рис. 20.1).

Обратная величина константы скорости реакции первого порядка имеет физический смысл средней продолжительности жизни отдельной молекулы.

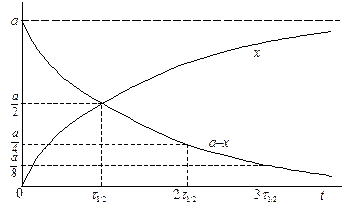Рис.20.1. Зависимость концентраций прореагировавшего и оставшегося вещества от времени

Другой важной характеристикой реакции является время полуреакции(период полураспада) t_1/2 – время, в течение которого прореагирует половина исходного количества вещества. Подставляя в уравнение (20.8) значения t = t_1/2 и x = a/2, получаем:

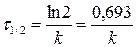. (20.13)

Как видно из уравнения, период полуреакции не зависит от исходного количества взятого вещества, а определяется только значением константы скорости реакции.

Из полученных уравнений следует также, что полностью вещество прореагирует только через бесконечно большой промежуток времени (x ® a при t ® ¥). Практически реакцию считают закончившейся, когда аналитически невозможно уже определить присутствие исходного вещества в системе или изменения во времени концентрации продуктов, т.е. практическое время реакции зависит от чувствительности используемых методов анализа.

20.3.2. Односторонние реакции второго порядка

В качестве примеров реакций второго порядка можно привести реакции образования йодоводорода в газовой фазе (или его разложения)

H₂ + I₂ ® 2HI,

омыления эфира щелочью

CH₃COOC₂H₅ + NaOH ® CH₃COONa + C₂H₅OH,

разложения оксида азота (IV)

2NO₂ ® 2NO + O₂

По второму порядку протекают многочисленные элементарные бимолекулярные реакции с участием атомов и свободных радикалов, являющиеся промежуточными стадиями химических реакций.

Рассмотрим реакцию второго порядка, которая протекает по уравнению:

n₁А + n₂В ® продукты

Если в начальный момент времени (t = 0) концентрации веществ А и В равны соответственно a и b, и через некоторое время t концентрация А уменьшилась на x, то скорость реакции

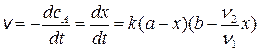. (20.14)

После разделения переменных получим:

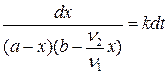. (20.15)

В наиболее простом случае, когда исходные концентрации веществ равны (a = b) и n₁ = n₂, уравнение (20.15) принимает вид

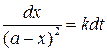. (20.16)

Интегрируя его в пределах от x = 0 до x (левая часть) и от t = 0 до t (правая часть), получим кинетическое уравнение реакции второго порядка:

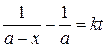(20.17)

или

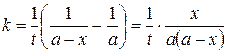. (20.18)

Отсюда видно, что в размерность константы скорости входят величины, обратные времени и концентрации, т.е. численное значение константы зависит от выбора единиц времени и концентрации.

В рассматриваемом случае возможно также использование понятия времени полуреакции. Подставив в уравнение (20.17) t = t_1/2 и x = a/2, получим для времени полуреакции

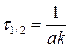. (20.19)

Таким образом, для реакции второго порядка период полуреакции зависит не только от значения константы скорости, но и от начальной концентрации веществ.

Для решения уравнения (20.15) в общем случае, когда a ¹ b, n₁ ¹ n₂ , представим левую часть соотношения в виде суммы двух дробей с коэффициентами С₁ и С₂:

. (20.20)

Очевидно, что

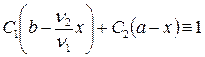. (20.21)

Это равенство справедливо при любых значениях x. Если поочередно подставить значения x = a и x = b в (20.21), то получим

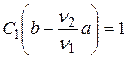и 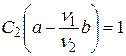. (20.22)

Используя полученные отсюда значения С₁ и С₂, проведем интегрирование уравнения (20.15):

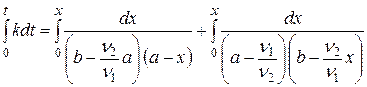. (20.23)

Отсюда константа скорости реакции второго порядка равна:

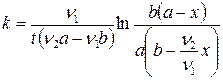. (20.24)

В весьма распространенных случаях, когда n₁ = n₂, получим

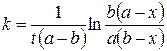. (20.25)

20.3.3. Реакции третьего порядка

Примерами реакций третьего порядка могут служить протекающая в газовой фазе реакция окисления оксида азота (II)

2NO + O₂ ® 2NO

или реакция восстановления хлорида железа (III) в растворе

2FeCl₃ + SnCl₂ ® 2FeCl₂ + SnCl₄ .

К ним также относятся процессы рекомбинации атомов и простых радикалов с участием третьей частицы, уносящей избыток энергии:

Н + Н + М ® Н₂ + М

СН + СН + М ® С₂Н₂ + М

Уравнение реакции третьего порядка можно записать в виде

А + В + С ® продукты

В простейшем случае, когда концентрации всех веществ одинаковы, т.е. c_A = c_B = c_C = a, скорость реакции равна

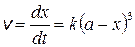, (20.26)

и после интегрирования получим:

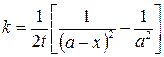. (20.27)

В общем случае, когда вещества имеют различные концентрации a, b, c, скорость реакции

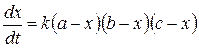. (20.28)

Интегрируя это уравнение тем же способом, что и в случае реакции второго порядка, получим кинетическое уравнение:

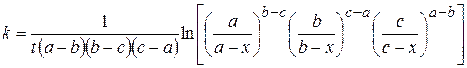. (20.29)

20.3.4. Реакции n-ого порядка

Для реакции произвольного n-ого порядка (кроме n = 1) при одинаковых концентрациях всех реагирующих веществ, равных a, скорость

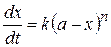, (20.30)

что после разделения переменных и интегрирования дает

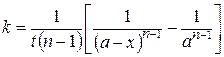. (20.31)

В таком виде формула не пригодна для описания кинетики реакций первого порядка, так при n = 1 возникает неопределенность; раскрытие неопределенности приводит к уравнению (20.10).

Подставляя в уравнение (20.30) t = t_1/2 и x = a/2, придем к выражению для периода полуреакции:

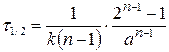. (20.32)

20.4. Методы определения порядка реакции

При определении порядка реакции вначале находят порядок по каждому из реагирующих веществ. Для этого концентрации всех веществ, кроме рассматриваемого, берутся в большом избытке, так, что их можно считать постоянными и ввести в константу скорости. Используя какие-либо методы анализа, определяют концентрации исследуемого вещества через различные промежутки времени. Для того, чтобы концентрация вещества не изменилась во время взятия пробы и проведения анализа, реакцию затормаживают (“замораживают”) – охлаждают реакционную смесь, вводят специальные реактивы и т.п. Существует много различных способов определения порядка, наиболее распространенные из которых мы рассмотрим.

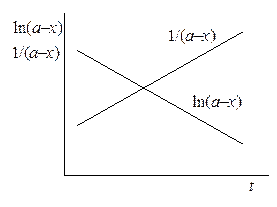Рис.20.3. Определение порядка реакции методом графического подбора

1. Метод графического подбора. Как следует из уравнения (20.10) для реакции первого порядка выполняется линейная зависимость в координатах логарифм концентрации – время. Для реакций второго порядка такая зависимость наблюдается в координатах 1/(a – x) – t (уравнение (20.17)), а для реакций n-ого порядка прямая получается в координатах 1/(a – x) – время (уравнение (20.30)). Таким образом, используя полученные в эксперименте значения концентраций в различные моменты времени, строят графики в тех или координатах до получения линейной зависимости.

2. Метод аналитического подбора уравнения заключается в том, что проводится расчет константы скорости путем подстановки экспериментальных данных в различные кинетические уравнения. Если уравнение выбрано правильно, константа скорости должна оставаться постоянной в пределах ошибок опыта не зависимо от времени; систематический ход константы скорости свидетельствует о том, что уравнение выбрано неверно.

3. Определение порядка по периоду полуреакции. Логарифмируя уравнение (20.31) для периода полуреакции, получим:

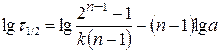. (20.33)

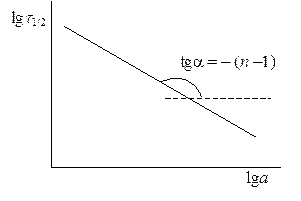Рис.20.4. Определение порядка по периоду полуреакции

Это линейная зависимость в координатах lgt_1/2 – lga. Построив график в этих координатах (рис. 20.3) по тангенсу угла наклона прямой определяем порядок реакции. Отрезок, отсекаемый прямой на оси ординат равен 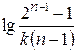, откуда можно рассчитать константу скорости реакции k.

4. Графический метод определения порядка. Скорость реакции n-ого порядка по данному веществу равна

v = kcⁿ или

lgv = lgk + nlgc, (20.34)

где c – текущая концентрация реагирующего вещества.

Для определения порядка вначале строят график зависимости концентрация – время. Проводя касательные к кривой в точках, соответствующим различным моментам времени t₁, t₂, …, находят по тангенсу угла наклона касательных скорости реакции v₁, v₂, … в эти моменты времени (рис. 20.5a). Затем логарифмы скоростей откладывают как функции логарифмов соответствующих концентраций c₁, c₂,.... Согласно уравнению (20.25) должна получиться прямая, тангенс угла наклона которой равен порядку реакции, а отсекаемый на оси ординат отрезок – логарифму константы скорости (рис. 20.5б).

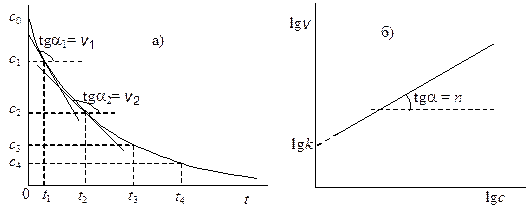Рис.20.5. Определение порядка реакции графическим методом: a) нахождение скорости; б) нахождение порядка и константы скорости

Существуют также другие методы определения порядка реакций. Для надежного определения нахождения этой величины обычно необходимо использовать несколько методов.

20.5. Сложные реакции

К сложным реакциям относят процессы, в которых одновременно протекает несколько реакций (обратимые, параллельные, последовательные, сопряженные и т.п.)

Для описания кинетики сложных реакций используют принцип независимости, согласно которому при протекании в системе нескольких реакций каждая из них протекает независимо от других и подчиняется основному закону кинетики. Следует заметить, что этот принцип не является абсолютно строгим и не выполняется, например, для сопряженных реакций.

20.5.1. Обратимые реакции первого порядка

К обратимым (двусторонним) реакциям первого порядка относятся реакции изомеризации, например, изомеризация цианида аммония в мочевину в водном растворе

NH₄CNO L (NH₂)₂CO

или мутаротация глюкозы

a-глюкоза L b-глюкоза.

Уравнение таких реакций в общем виде можно представить в форме

k₁

А L В ,

k₂

где k₁ и k₂ – константы скоростей прямой и обратной реакций.

Так как рассматриваемая реакция протекает в противоположных направлениях, то ее общая скорость равна разности скоростей прямой и обратной реакций:

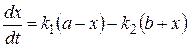, (20.35)

где a и b – исходные количества веществ А и В, x – количество вещества А, прореагировавшего к моменту времени t.

Преобразуем уравнение (20.35) к виду:

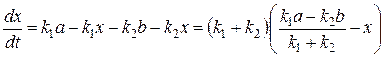. (20.36)

К моменту установления равновесия прореагирует x_¥ молей вещества А, а скорость реакции в состоянии равновесия равна нулю. Из этих условий следует, что

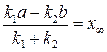, (20.37)

и уравнение (20.36) принимает вид:

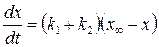. (20.38)

Разделяя переменные и интегрируя в пределах от 0 до t и от 0 до x, получим:

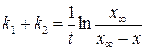. (20.39)

По этой формуле можно определить лишь сумму констант скоростей k₁ и k₂. Для раздельного нахождения этих констант воспользуемся условием равновесия:

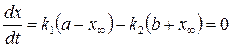. (20.40)

Отсюда

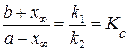, (20.41)

где K_c – константа равновесия.

Совместное решение уравнений (20.29) и (20.30) позволяет вычислить константы скоростей прямой и обратной реакций k₁ и k₂.

В случае более сложных обратимых реакций (второго, третьего порядков) можно использовать такой же подход, однако сложность математической обработки, естественно, возрастает.

20.5.2. Параллельные реакции

В случае параллельных реакций одни и те же вещества реагируют одновременно по нескольким направлениям, образуя разные продукты. Например, при нитровании фенола одновременно образуются орто-, мета- и пара-нитрофенолы.

Рассмотрим простейший случай двух параллельных необратимых реакций первого порядка:

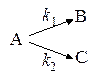
Используя принцип независимости, запишем выражение для скорости реакции превращения вещества А в В и С:

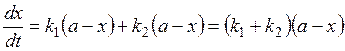. (20.42)

После его интегрирования получим

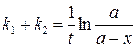(20.43)

или

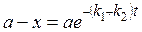. (20.44)

Эти уравнения совпадают с уравнениями (20.10) и (20.11) для необратимой реакции первого порядка с той разницей, что вместо одной константы скорости k получаем сумму констант k₁ и k₂. Чтобы найти отдельные значения k₁ и k₂, запишем уравнения для скоростей образования веществ В и С (c_B и c_C – текущие концентрации этих веществ):

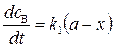и 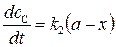. (20.45)

Подставим сюда значение (a – x) из уравнения (20.44). Тогда

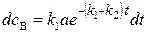. (20.46)

Интегрируя это уравнение в пределах от 0 до c_B и от 0 до t, получим

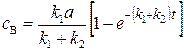. (20.47)

Аналогично для вещества С:

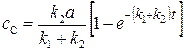. (20.48)

Из последних двух уравнений следует, что

c_B/c_C = k₁/k₂, (20.49)

т.е. в любой момент реакции отношение концентраций продуктов является постоянной величиной, равной отношению констант скоростей параллельных реакций. Совместное решение уравнений (20.31) и (20.33) позволяет вычислить эти константы k₁ и k₂.

20.5.3. Последовательные реакции

Как было сказано выше, большинство химических реакций имеет сложный механизм и они проходят через ряд последовательных стадий, а конечные продукты образуются из неустойчивых промежуточных продуктов – молекул, атомов, свободных радикалов. В связи с этим исследование таких последовательных (консекутивных) реакций представляет очень важную задачу химической кинетики.

Наиболее простым для рассмотрения является случай двух последовательных необратимых реакций первого порядка:

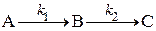
В начальный момент времени t = 0 концентрация вещества А равна a, вещества В и С отсутствуют. К некоторому моменту времени t концентрации веществ равны соответственно: c_A = a – x; c_B = x – y; c_C = y.

Скорость превращения вещества А в В равна

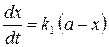, (20.50)

а скорость образования вещества С из В

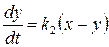. (20.51)

Решение первого уравнения было рассмотрено ранее (см. раздел 20.3.1):

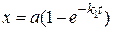. (20.52)

Подставляя это значение во второе уравнение, получим:

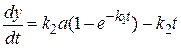. (20.53)

Временно приравняем первый член правой части этого уравнения нулю:

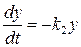або 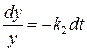. (20.54)

После интегрирования получаем

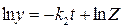, (20.55)

где Z – условная константа интегрирования. Тогда

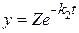. (20.56)

В действительности Z не является постоянной, а зависит от времени. Поэтому продифференцируем уравнение (20.56), считая Z функцией времени:

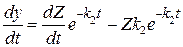. (20.57)

Учитывая значение y из уравнения (20.55), видим, что

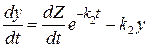. (20.58)

Сравнивая последнее уравнение с уравнением (20.53), находим, что

. (20.59)

После интегрирования находим

. (20.60)

где I – постоянная интегрирования.

Полученное значение Z подставляем в уравнение (20.56):

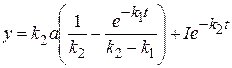. (20.61)

Постоянную интегрирования находим из условия, что в начальный момент времени при t = 0 концентрация вещества С y = 0:

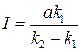. (20.62)

и, окончательно, получаем зависимость концентрации конечного продукта от времени:

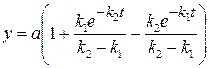. (20.63)

Зависимость концентрации промежуточного продукта от времени найдем, используя величины x и y:

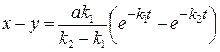. (20.64)

Из уравнения (20.63) следует, что концентрация конечного продукта в пределе стремится к исходной концентрации вещества А (при t ®¥ y® a), т.е. исходное вещество полностью превращается в продукт С.

Концентрация промежуточного продукта проходит через максимум, так как согласно уравнению (20.64) при t = 0 (x – y) = 0 и при t ®¥ (x – y)® 0, а в любой другой момент времени концентрация (x – y) >0.

Время достижения максимума t_макс можно определить из условия экстремума:

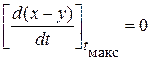. (20.65)

Продифференцируем уравнение (20.64):

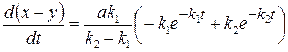. (20.66)

В соответствии с условием (20.65)

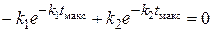. (20.67)

После логарифмирования и решения этого уравнения относительно t получим

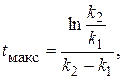(20.68)

т.е. время достижения максимума зависит не только от отношения констант скоростей k₂ и k₁ , но и от их абсолютных значений.

Схематически характер изменения концентраций веществ во времени представлен на рисунке 20.5.

Максимальная концентрация промежуточного продукта

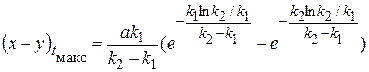. (20.69)

Если ввести обозначение k₂ /k₁ = q, то

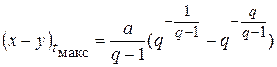. (20.70)

Рис. 20.5. Зависимость концентрации веществ от времени в последовательных реакциях

Отсюда следует, что максимальная концентрация промежуточного продукта зависит только от соотношения констант скоростей k₂ и k₁ .

Если промежуточный продукт сравнительно устойчив, т.е. k₁>> k₂ , величина q очень мала (q << 1) и ею можно пренебречь по сравнению с единицей. В этих условиях

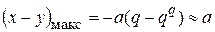, (20.71)

т.е. почти все исходное вещество накапливается в виде промежуточного продукта. Это вполне естественно, так как промежуточное вещество В превращается в конечное С с очень малой скоростью, и в пределе при k₂ ® 0 вторая реакция не идет.

Если промежуточный продукт очень неустойчив, k₂ >> k₁ , q >> 1, в уравнении (20.70) можно пренебречь единицей по сравнению с q, тогда

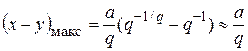. (20.72)

Так как величина q велика, то концентрация промежуточного продукта очень мала.

Кривая y = f(t), показывающая изменение концентрации конечного продукта С в ходе реакции, имеет S-образный характер. В начальный период скорость образования конечного продукта мала и его количество настолько незначительно, что аналитически не обнаруживается. Этот начальный период реакции называют индукционным. После индукционного периода концентрация конечного продукта вначале увеличивается медленно, затем все быстрее, но через некоторое время скорость образования вновь уменьшается, т.е. на кривой имеется точка перегиба. Для нахождения момента времени, соответствующего точке перегиба, приравняем вторую производную уравнения (20.62) нулю, откуда найдем эту точку:

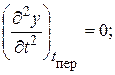
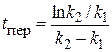, (20.73)

т.е. точка перегиба совпадает со временем достижения максимальной концентрации промежуточного продукта.

20.6. Метод стационарных концентраций

В рассмотренном выше простейшем случае двух последовательных реакций первого порядка получены уравнения для концентрации промежуточного и конечного продуктов, которые нельзя строго решить относительно констант скорости, т.е. невозможно рассчитывать последние непосредственно из экспериментальных данных о зависимости концентрации от времени. В более сложных случаях нескольких последовательных реакций разного порядка строгое математическое описание кинетики часто оказывается невозможным.

Для описания кинетики многостадийных реакций можно использовать приближенный метод стационарных концентрацийБоденштейна. В основе метода лежит положение о том, что через некоторое небольшое время после начала реакции скорость образования промежуточного продукта становится примерно равной скорости его распада и суммарную скорость изменения концентрации неустойчивого промежуточного продукта можно считать приблизительно равной нулю в течение достаточно длительного времени, т.е. в течение этого времени устанавливается стационарная концентрация неустойчивого продукта.

Рассмотрим, например, некоторую реакцию

А + В ® 2С,

которая протекает с образованием двух промежуточных продуктов М₁ и М₂ по схеме:

1) А ® 2М₁ k₁

2) М₁ + В ® С + М₂ k₂

3) М₂ + А ® С + М₁ k₃

4) М₁ + М₁ ® А k₄

Обозначим через c_oA и c_oB исходные концентрации веществ А и В, через c_i – текущие концентрации всех участников реакции. Используя предложенную схему реакции, запишем выражения для уменьшения концентраций А и В и увеличения концентрации С с течением времени:

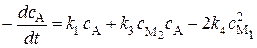, (20.74)

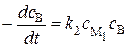, (20.75)

. (20.76)

Скорости изменения концентрации промежуточных продуктов М₁ и М₂ соответственно равны:

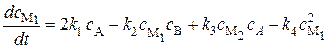, (20.77)

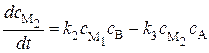. (20.78)

Считая, что концентрации промежуточных продуктов 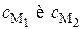в течение реакции малы и учитывая стехиометрическое уравнение, можно записать:

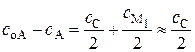, (20.79)

. (20.80)

Тогда, после дифференцирования по времени, получим:

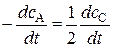, (20.81)

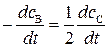. (20.82)

Подставим в уравнение (20.81) значения скоростей (20.74) и (20.77):

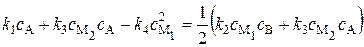(20.83)

или

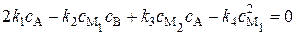. (20.84)

Последнее выражение совпадает с уравнением (20.77) для скорости образования промежуточного продукта М₁, откуда следует, что

. (20.85)

Аналогично, подставив в уравнение (20.82) значения скоростей (20.74) и (20.75) и сравнивая с (20.77), получим

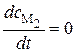. (20.86)

Уравнения (20.85) и (20.86) и являются выражениями принципа стационарности.

В заключение заметим, что метод стационарных концентраций не является совершенно строгим, его применение ограничивается выполнением условий типа (20.78), (20.79), т.е. образованием очень неустойчивых промежуточных продуктов, концентрация которых в ходе реакции оказывается небольшой. Однако на практике такие случаи встречаются очень часто (образование в качестве промежуточных продуктов атомов, свободных радикалов), поэтому метод стационарных концентраций получил широкое распространение при изучении кинетики и механизма различных реакций.

20.7. Влияние температуры на скорость химических реакций

В большинстве случаев повышение температуры приводит к увеличению константы скорости химической реакции. Согласно правилу Вант-Гоффатемпературный коэффициент скорости g, т.е. отношение констант скоростей реакции при температурах T и T + 10, изменяется в пределах от 2 до 4:

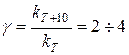. (20.87)

В общем случае изменения температуры от T до T + 10n, где n – положительное или отрицательное, целое или дробное число, для температурного коэффициента можно записать:

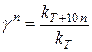. (20.88)

Правило Вант-Гоффа получено эмпирически и является приближенным. Значения температурного коэффициента не остаются постоянными при изменении температуры и стремятся к единице при высоких температурах. Поэтому правило можно использовать для полуколичественных оценок в области сравнительно низких температур.

Более точно зависимость константы скорости от температуры передается уравнением Аррениуса:

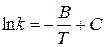, (20.89)

где В и С – постоянные, характерные для данной реакции и не зависящие от температуры.

Уравнение Аррениуса также было получено вначале эмпирически, а затем обосновано теоретически.

При выводе уравнения Аррениус предположил, что реагировать могут не все молекулы, а лишь некоторые из них, находящиеся в особом активном состоянии. Эти молекулы образуются из обычных в эндотермическом процессе с поглощением тепла E_A. Так, например, в реакции

A ® B

активные молекулы А* образуются из нормальных молекул А по схеме:

A L A* + E_A

По Аррениусу, этот процесс является обратимым и быстрым, так что в системе всегда сохраняется термодинамическое равновесие между А и А*, которое можно характеризовать константой равновесия K_c:

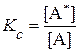или [A*] = K_c[A]. (20.90)

Предполагается, что концентрация активной формы мала, и равновесная концентрация [А] исходных молекул А практически равна текущей концентрации c_A » [А]. Изменение константы равновесия с температурой описывается уравнением изохоры Вант-Гоффа

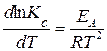. (20.91)

Последнее допущение Аррениуса заключается в том, что превращение активных молекул в конечный продукт осуществляется со скоростью, не зависящей от температуры и относительно медленно:

[A*] ® B

Таким образом, скорость образования вещества В равна

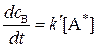, (20.92)

где k’ – константа скорости, не зависящая от температуры.

С другой стороны, согласно основному постулату химической кинетики скорость реакции А ® В равна

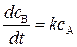, (20.93)

где k – определяемая экспериментально константа скорости, которая зависит от температуры.

Сравнивая уравнения (20.92) и (20.93) и учитывая все ранее сделанные допущения, получим:

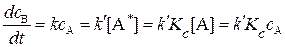. (20.94)

Отсюда следует, что экспериментальная константа скорости

k = k'c або lnk = lnk' + lnK_c. (20.95)

Так как k’ не зависит от температуры, то дифференцируя по T, получим

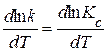. (20.96)

Используя уравнение Вант-Гоффа (20.91), приходим к уравнению Аррениуса в дифференциальной форме:

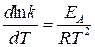. (20.97)

Величина E_A называется энергией активации, или опытной энергией активации. В рамках изложенных представлений – это то количество теплоты, которое необходимо, чтобы перевести один моль молекул, находящихся в нормальном состоянии, в особую активную, реакционно-способную форму.

Интегрируя уравнение (20.96) в предположении независимости энергии активации от температуры, получим:

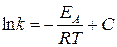, (20.98)

где С – константа интегрирования.

Полученное уравнение совпадает с эмпирическим уравнением Аррениуса (20.89), в котором постоянная В соответствует значению E_A/R или E_A = ВR. Потенцируя уравнение (20.98), можно представить его в экспоненциальной форме, полагая e^C = A:

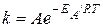. (20.99)

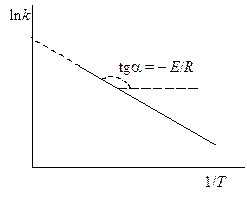Рис. 20.6. Зависимость lnk от 1/T

Рис. 20.7. Зависимость lnk от 1/T для параллельных реакций

Как видно из уравнения (20.97), логарифм константы скорости является линейной функцией обратной температуры. Поэтому для экспериментального определения E_A находят константы скорости реакции при нескольких температурах и строят зависимость в координатах lnk – 1/T (рис. 20.6). Отрезок, отсекаемый прямой на оси ординат, равен константе С, а энергия активации вычисляется по тангенсу угла наклона прямой.

Если известны константы скорости реакции только при двух температурах T₁ и T₂, энергию активации можно вычислить из соотношения, которое получается интегрированием уравнения (20.97) в пределах этих температур:

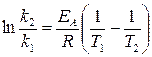, (20.100)

где k₁ и k₂ – константы скорости при температурах T₁ и T₂ соответственно.

В некоторых случаях график зависимости lnk – 1/T имеет иной вид – он состоит как бы из двух пересекающихся прямых с разным наклоном, что свидетельствует о сложном характере реакции. Например, водород может реагировать как с жидкой, так и с газообразной серой. Если в сосуде одновременно присутствуют водород, жидкая сера и ее пары, то при низких температурах протекает реакция водорода с жидкой серой с меньшей энергией активации (отрезок 1 на рис. 20.7), а при более высоких температурах – реакция водорода с парами серы с большей энергией активации (отрезок 2).

Экспериментальные исследования показывают, что энергии активации реакций с валентнонасыщенными молекулами составляют от нескольких десятков до сотен (50 ¸ 500) кДж/моль. При этом не обнаружено каких-либо простых закономерностей, связывающих энергию активации с какими-нибудь другими характеристиками реакции, например, с тепловым эффектом. В реакциях, протекающих через элементарные стадии с участием свободных атомов и радикалов, энергии активации значительно ниже (10 ¸ 50 кДж/моль).

В некоторых случаях повышение температуры приводит к снижению скорости реакции. Примером может служить реакция

2NO + O₂ ® 2NO₂ ,

которая является одной из стадий получения азотной кислоты. Аномальный ход температурной зависимости константы скорости этой реакции можно объяснить, предположив, что она протекает в две стадии:

I. 2NO L N₂O₂ (быстрая, обратимая, экзотермическая)

II. N₂O₂ + O₂ ® 2NO₂ (медленная)

Общая скорость реакции определяется скоростью второй, более медленной стадии:

.

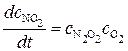Концентрация димера N₂O₂ зависит от константы равновесия, устанавливающегося на первой стадии:

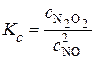или .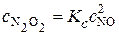

Тогда

.

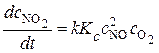Это уравнение соответствует экспериментально установленному третьему порядку реакции. Так как первая стадия экзотермична, то константа равновесия K_c уменьшается при повышении температуры. Если это уменьшение перекрывает возможное увеличение k, то это и приведет к общему снижению скорости реакции.

20.8 Гетерогенные химические реакции

Химическое взаимодействие в гетерогенных системах осуществляется на поверхности раздела фаз: твердое тело – газ, твердое тело – жидкость (раствор) или жидкость – жидкость в случае несмешивающихся жидкостей. Скорость гетерогенного процесса определяется как количество вещества, реагирующего в единицу времени на единице площади поверхности:

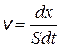, (20.101)

где S – площадь поверхности, на которой проходит реакция. Нахождение истинного значения площади поверхности представляет сложную задачу вследствие шероховатости поверхности, наличия пор, капилляров.

В гетерогенном процессе можно выделить три основных этапа: подвод реагирующего вещества к поверхности раздела, взаимодействие на поверхности (которое может состоять из нескольких стадий), отвод продуктов реакции в объем фазы. Скорость всего процесса в целом определяется скоростью наиболее медленной стадии, которой может быть любой из названных этапов.

Подвод реагентов к поверхности и отвод продуктов осуществляется при молекулярной или конвективной диффузии. Диффузия описывается законом Фика:

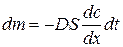, (20.102)

где dm – количество вещества, продиффундировавшего за время dt через поверхность S, dc/dx – градиент концентрации.

Если концентрация вещества на границе раздела фаз равна c_s, а на некотором расстоянии d – c_x, то градиент концентраци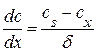и

и 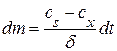. (20.103)

Разделив последнее уравнение на объем V и переходя к концентрациям, получим:

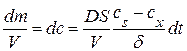. (20.104)

Скорость диффузии равна

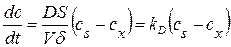. (20.105)

Полученное уравнение соответствует кинетическому уравнению реакции первого порядка. Таким образом, если лимитирующей стадией является диффузия, то кинетика реакции будет описываться уравнением (20.70), хотя оно и не отражает истинной скорости и порядка химической реакции на поверхности. В таком случае говорят, что процесс идет в диффузионной области.

Если скорость химической реакции значительно меньше, чем скорость диффузии, процесс протекает в кинетической областии описывается уравнением той реакции, которая идет на поверхности.

При сравнимых скоростях диффузии и реакции процесс идет в переходной области. Константу скорости в зависимости от температуры можно выразить уравнением:

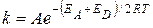, (20.106)

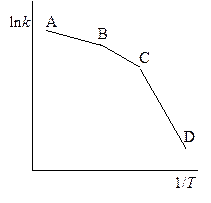Рис. 20.8. Температурная зависимость константы скорости гетерогенной химической реакции

где E_A – энергия активации химической реакции, E_D – энергия активации диффузии.

Величина E_D небольшая (5 ¸ 10 кДж/моль), т.е. E_D << E_A , поэтому экспериментально определяемая энергия активации примерно в два раза меньше истинной энергии активации химической реакции.

Так как энергия активации диффузии невелика, то при изменении температуры на 10° скорость диффузии изменяется в 1,1 – 1,2 раза, в то время как скорость химической реакции меняется в 2 – 4 раза. Поэтому при определениях скорости реакции в широком диапазоне температур наблюдается сложный характер зависимости lnk от 1/T (рис. 20.8).

При низких температурах реакция идет обычно в кинетической области (участок CD) и скорость сильно зависит от температуры. При высоких температурах скорость диффузии обычно значительно меньше скорости химической реакции, процесс идет в диффузионной области с мало изменяющейся скоростью (участок AB). Участок BC соответствует переходной области.

Значительную роль в кинетике гетерогенных реакций может играть скорость отвода продуктов реакции. Если, например, в реакции образуются труднорастворимые вещества, то, осаждаясь на поверхности, они блокируют ее, и реакция практически прекращается.