Волноводы и резонаторы

Электрическая энергия от источников энергии передается потребителям с помощью различных каналов. В области сверхвысоких частот (порядка 10⁹ Гц) в качестве таких каналов широко применяются различного вида волноводы. Так как при передаче информации по существу также необходимо передавать энергию, волноводы можно рассматривать как каналы связи для передачи информации сигналами, спектр которых лежит в области сверхвысоких частот (СВЧ).

Наибольшее распространение в технике получили полые волноводы прямоугольного сечения. Пространство, в котором распространяется волна, в этом случае ограничено четырьмя плоскими проводящими стенками (рис. 7.8).

Рис. 7.8. Волновод прямоугольного сечения

Энергия от источника передается в волновод с помощью небольших антенн в виде одного или нескольких штырьков или рамок. В зависимости от вида антенн, их числа и расположения в волноводе возникают колебания (волны) различного типа. Однако все эти волны должны удовлетворять граничным условиям. Это требование выполняется, если решение для вектора электрического поля представить в виде:

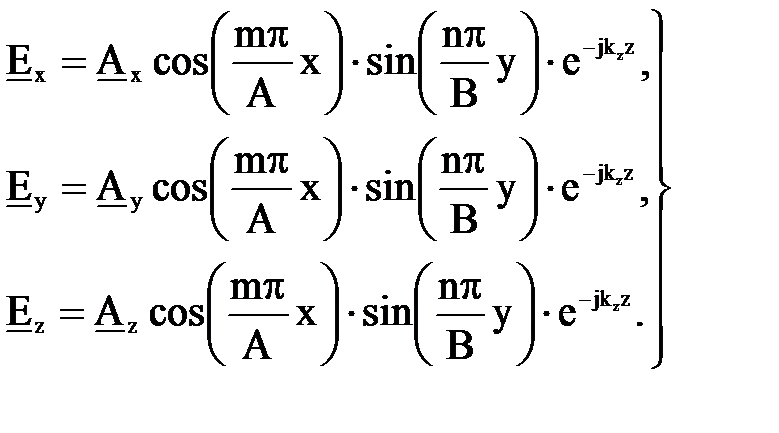(7.35)

где A_x, A_y и A_z - постоянные интегрирования, А и В - поперечные размеры волновода, a m и n - целые числа. Эти числа называются характеристическими числами.

Характерным для решения (7.35) является то, что в направлениях, перпендикулярных стенках волновода, образуются стоячие волны, а в направлении оси волновода – бегущая волна, характеризуемая множителем 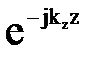(если знак минус заменить на плюс, получим поле обратной бегущей волны .

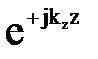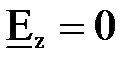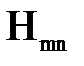Выражения (7.35) определяют все типы воли, которые могут существовать в волноводах прямоугольного сечения. В основу классификации этих волн и их обозначения положены следующие принципы. Если отсутствует продольная составляющая напряженности электрического поля, т. е. , волны называются поперечно-электрическими (обозначаются ) или магнитными ( ). Если отсутствует продольная составляющая напряженности магнитного поля, т. е. , волны называются поперечно-магнитными (обозначаются 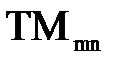) или электрическими ( 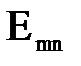). Нижние индексы приведенных обозначений соответствуют значениям характеристических чисел. Естественно, что чем меньше характеристические числа, тем проще структура поля.

Рассмотрим волну наиболее простой структуры - (m=0, n=1). В соответствии с (7.35), у волны этого типа будет только одна составляющая напряженности электрического поля ( 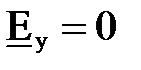, 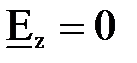). Если принять 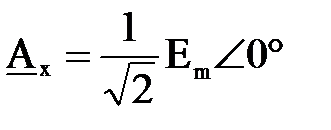, то

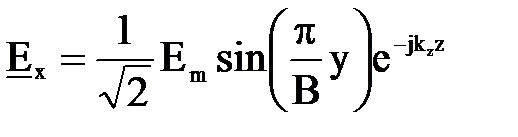(7.36)

или для мгновенного значения

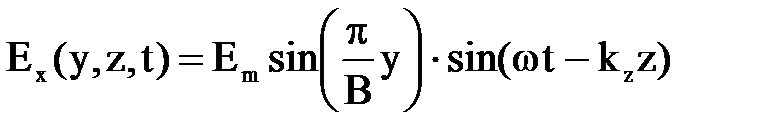. (7.37)

Из полученных выражений видно, что картина поля не изменяется по высоте волновода (поле не зависит от координаты х). Амплитуда напряженности электрического поля имеет максимальное значение в среднем сечении волновода, т. е. при у=В/2. На рис. 7.9 представлены эпюра распределения напряженности электрического поля по оси у при 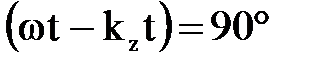и по оси z при у=В/2.

Рис. 7.9. Эпюры распределения напряженности электрического поля волны типа

Напряженность магнитного поля можно вычислить из второго уравнения Максвелла ( 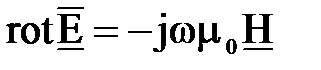), подставив в него полученные выше составляющие вектора 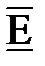, т. е. 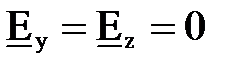, а 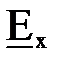из (7.36). Легко убедиться, что 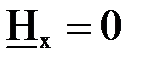, а

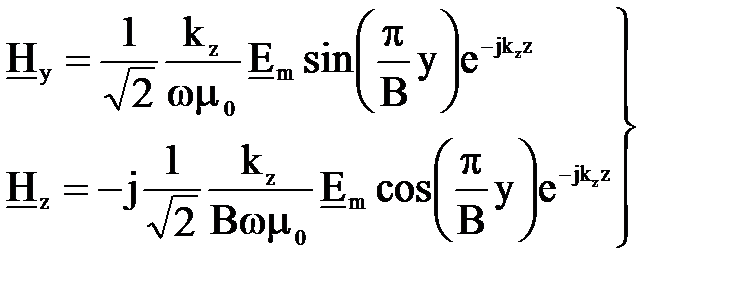. (7.38)

Легко проверить, что решение (7.35) будет удовлетворять уравнениям Максвелла только в том случае, если

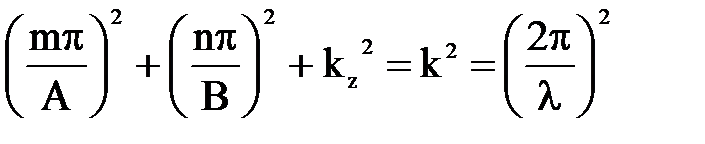, (7.39)

где 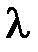- длина волны в свободном пространстве. Из (7.39) следует, что

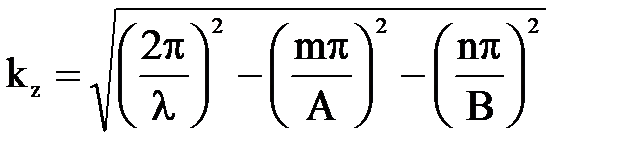. (7.40)

В направлении оси волновода уравнение поля определяется множителем 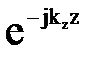. Для того чтобы в этом направлении поле представляло собой незатухающую бегущую волну, необходимо, чтобы 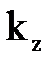было действительным числом. Следовательно, подкоренное выражение в (7.40) должно быть положительным, а это значит, что по волноводу нельзя передавать энергию на частотах, лежащих ниже некоторой критической частоты

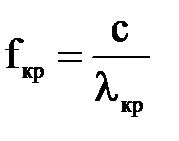. (7.41)

где 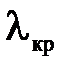- критическая длина волны в волноводе, которая определяется из условия равенства нулю подкоренного выражения в (7.40):

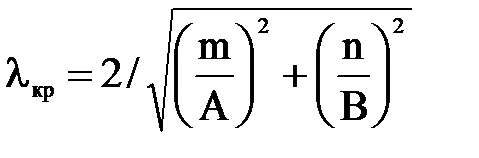. (7.42)

Если волновод закрыть с двух сторон, т. е. образовать металлическими стенками замкнутую полость, то стоячие волны могут образовываться по всем трем направлениям. Частоты колебаний, для которых возможно образование стоячих волн, для данной системы будут резонансными частотами системы. Сама система называется прямоугольным резонатором. Такие полые резонаторы широко применяются на СВЧ (сверхвысоких частотах), выполняя такие же функции, которые выполняют на более низких частотах резонансные контуры и фильтры.