Поверхностные эффекты при распространении радиоволн. Уравнения максвелла и их решения при заданных источниках
1. Магнитный поверхностный эффект.
В качестве примера распространения плоских электромагнитных волн в проводящей среде рассмотрим поле в стальном листе при прохождении вдоль листа переменного магнитного потока 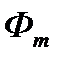 . Лист имеет толщину
. Лист имеет толщину 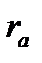 , высоту h, причем h>>
, высоту h, причем h>> 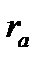 , большую протяженность в направлении перпендикулярном рисунку
, большую протяженность в направлении перпендикулярном рисунку
рис. 1 рис.2
Средняя плотность магнитного потока по сечению листа 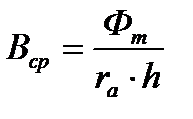
В силу симметрии напряженность магнитного поля на левой поверхности листа та же, что и на правой поверхности листа. Исследования показали, что распределение поля по сечению проводника неравномерно (рис. 2), это вызвано затуханием электромагнитной волны при ее распространении в проводящую среду. Этот эффект называется поверхностным эффектом. Если вдоль листа направлен магнитный поток, то поверхностный эффект называют магнитным. Если вдоль плоской шины направлен переменный ток, то – называют электрическим поверхностным эффектом. На рис.2 кривая H(Z) характеризует изменение модуля напряженности магнитного поля от Z. В средней плоскости листа Н до нуля не снижается. Кривая E(Z) характеризует изменение модуля электрического поля в функции от Z и проходит через ноль. Кривая плотности вихревых токов 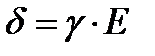 качественно повторяет кривую Е от Z ( разница только в масштабе).
качественно повторяет кривую Е от Z ( разница только в масштабе).
2. Поверхностный эффект в цилиндрическом проводе.
При протекании синусоидального электрического тока по цилиндрическому проводу так же наблюдается поверхностный эффект, заключающийся в неравномерности плотности тока 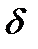 по сечению этого провода
по сечению этого провода
Плотность тока на оси провода определяется как формула (1).
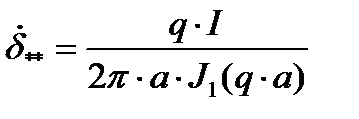
Где a – радиус кривизны
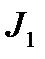 - функция Бесселя первого рода перового порядка
- функция Бесселя первого рода перового порядка
I – полное значение тока протекающего через провод
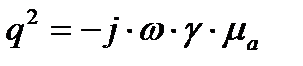
Плотность тока на поверхности провода определяется по формуле
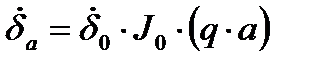 (2)
(2)
где 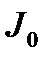 - функция Бесселя нулевого порядка первого рода.
- функция Бесселя нулевого порядка первого рода.
Сравнивая (1) и (2) имеем, что
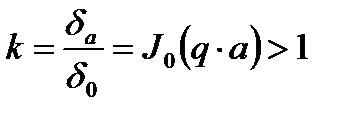
Отсюда следует, что плотность переменного тока на поверхности провода выше чем внутри.
Решение волновых уравнений для заданных источников.
Для тока или напряжения в однородной линии без потерь структура уравнения имеет вид 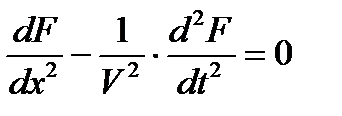 , а его решение как сумма двух волн: падающей и обратной.
, а его решение как сумма двух волн: падающей и обратной.
Решение записывается в виде 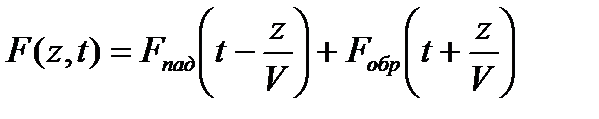
Падающая волна  распространяется в направлении оси
распространяется в направлении оси 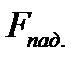 , обратная
, обратная 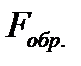 - в обратном направлении.
- в обратном направлении.
Положим, что векторный потенциал A применяется только по направлению оси z. Такая волна называется плоской электромагнитной волной. Волновое уравнение в этом случае будет иметь вид 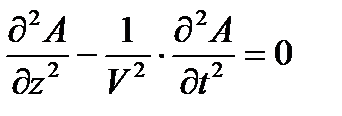 (2)
(2)
Решение уравнения (2) будет иметь вид:
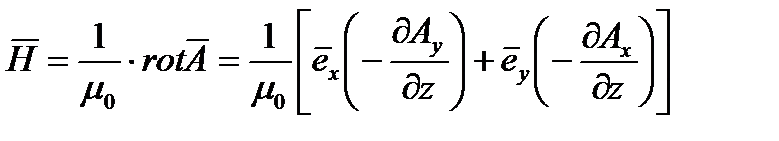
Где 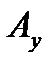 - проекция А на ось y
- проекция А на ось y
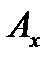 - проекция А на ось x
- проекция А на ось x
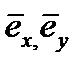 - орты.
- орты.
То есть вектор 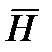 не имеет z составляющей. Вектор H выражается через Е
не имеет z составляющей. Вектор H выражается через Е
В случае плоской электромагнитной волны векторы Е и Н лежат в плоскости 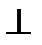 к оси Z. И для прямой обратной волны
к оси Z. И для прямой обратной волны
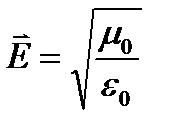
Переменное электромагнитное поле в однородной проводящей среде.
3. Уравнение Максвелла для проводящей среды.
Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью 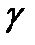 и магнитной проницаемостью
и магнитной проницаемостью 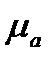 .
. 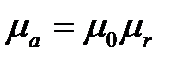 ;
; 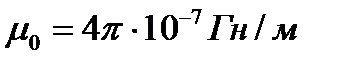
Первое и второе уравнение Максвелла записанное в комплексной форме для синусоидально изменяющихся во времени 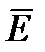 и
и 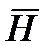 .
.
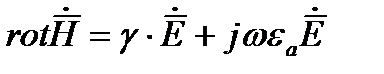 (1)
(1)
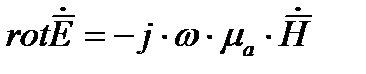 (2)
(2)
где 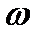 - круговая частота изменения векторов
- круговая частота изменения векторов 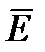 и
и 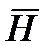
В проводящей среде даже при очень высоких частотах 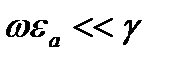
Поэтому с большой степенью точности слагаемым 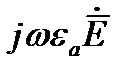 в первом уравнении Максвелла можно пренебречь. Таким образом первое и второе уравнение Максвелла для проводящих сред записываются как
в первом уравнении Максвелла можно пренебречь. Таким образом первое и второе уравнение Максвелла для проводящих сред записываются как
(1) 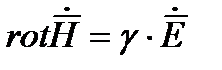 (2)
(2) 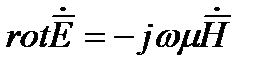
Решим эти уравнения относительно 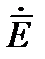 и
и 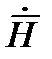 . С этой целью возьмем ротор от (1)
. С этой целью возьмем ротор от (1)
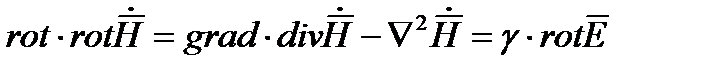
Учтем, что 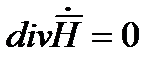 , поэтому
, поэтому 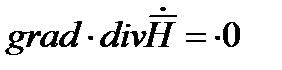 . Вместо
. Вместо 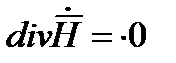 в соответствие с (2) подставим -.
в соответствие с (2) подставим -. 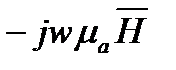 Получим
Получим
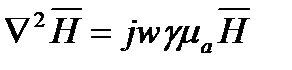 (3)
(3)
Данное уравнение является дифференциальным относительно 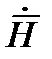 .
.
В общем случае, когда 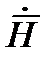 зависит от всех трех или даже от двух координат, решение этого уравнения очень сложно. Ограничимся рассмотрением решения данного уравнения для плоской электромагнитной волны.
зависит от всех трех или даже от двух координат, решение этого уравнения очень сложно. Ограничимся рассмотрением решения данного уравнения для плоской электромагнитной волны.
4. Плоская электромагнитная волна.
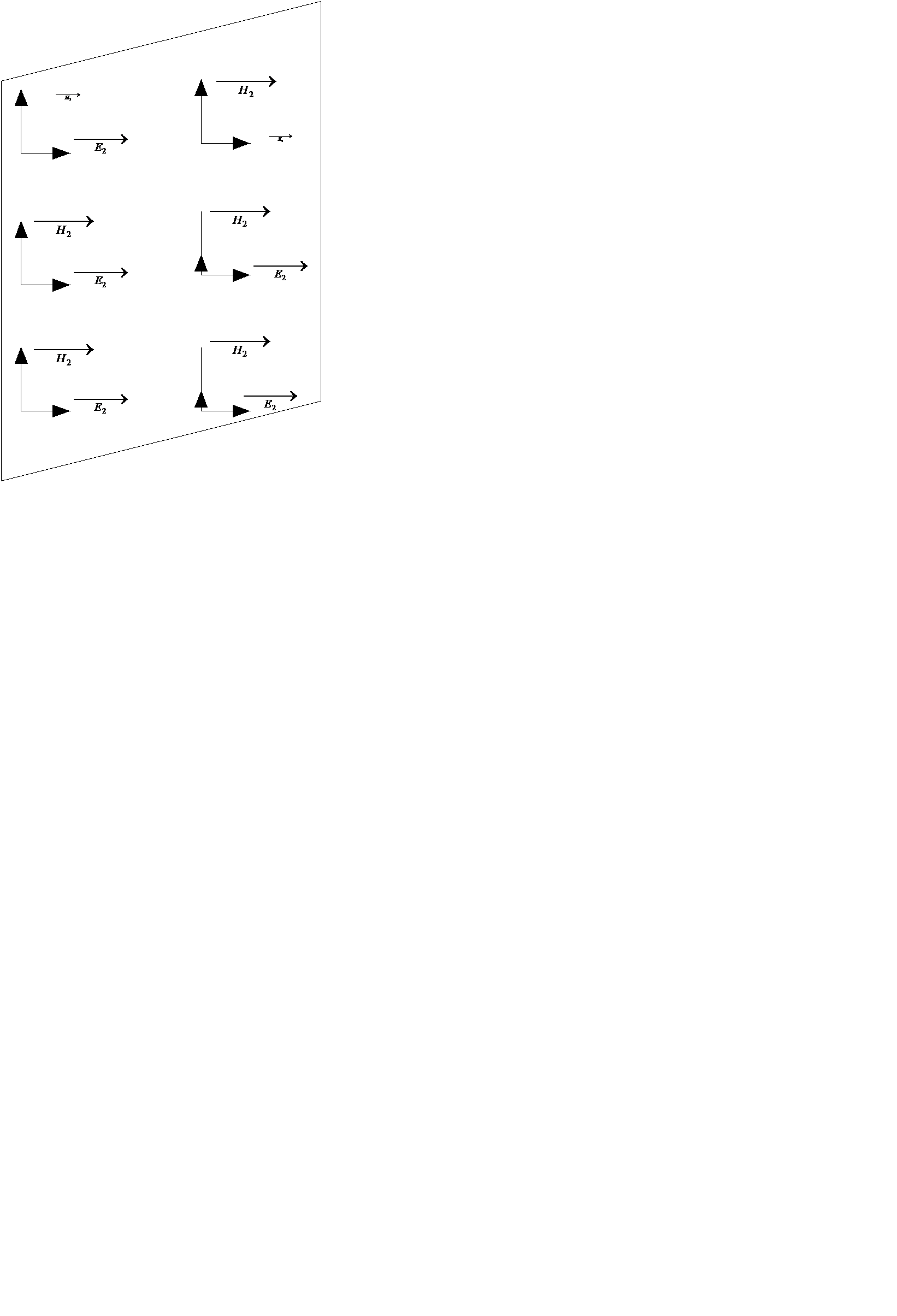 В общем случае под плоской электромагнитной волной понимают волну, векторы
В общем случае под плоской электромагнитной волной понимают волну, векторы 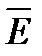 и
и 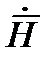 которые расположены в плоскости x o y , перпендикулярны направлению распространения волны ( ось z) и изменяющиеся только функции координаты z и времени t.
которые расположены в плоскости x o y , перпендикулярны направлению распространения волны ( ось z) и изменяющиеся только функции координаты z и времени t.
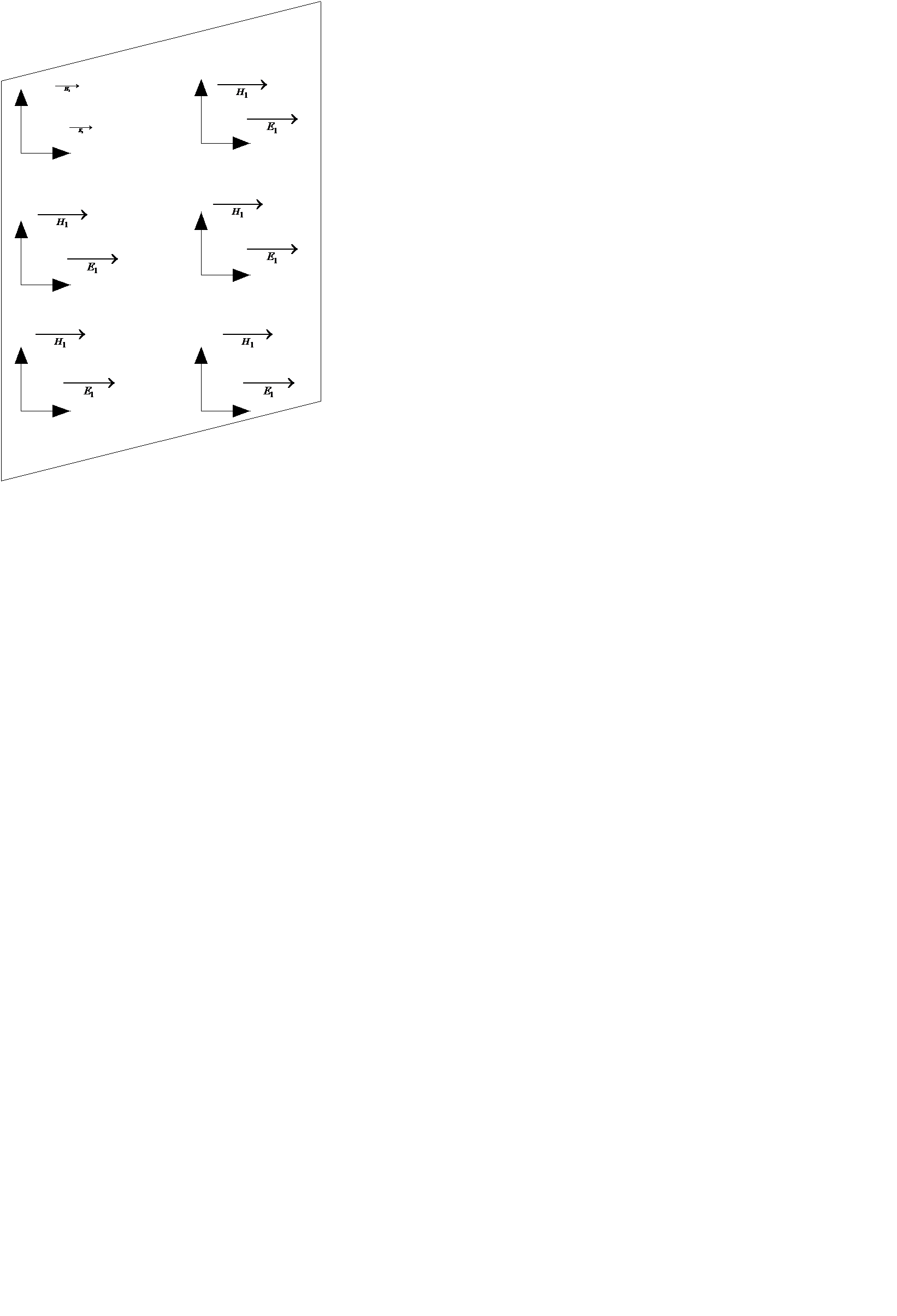
Рис.
На рисунке изображены для одного и того же момента времени векторы 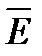 и
и 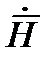 в двух параллельных плоскостях , перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости напряженности электрического и магнитных полей одинаковы по величине и направлении. Во всех точках второй плоскости напряженность электрического и магнитного полей также одинаковы по величине и направлению, но не равна напряженности поля в первой плоскости.
в двух параллельных плоскостях , перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости напряженности электрического и магнитных полей одинаковы по величине и направлении. Во всех точках второй плоскости напряженность электрического и магнитного полей также одинаковы по величине и направлению, но не равна напряженности поля в первой плоскости.
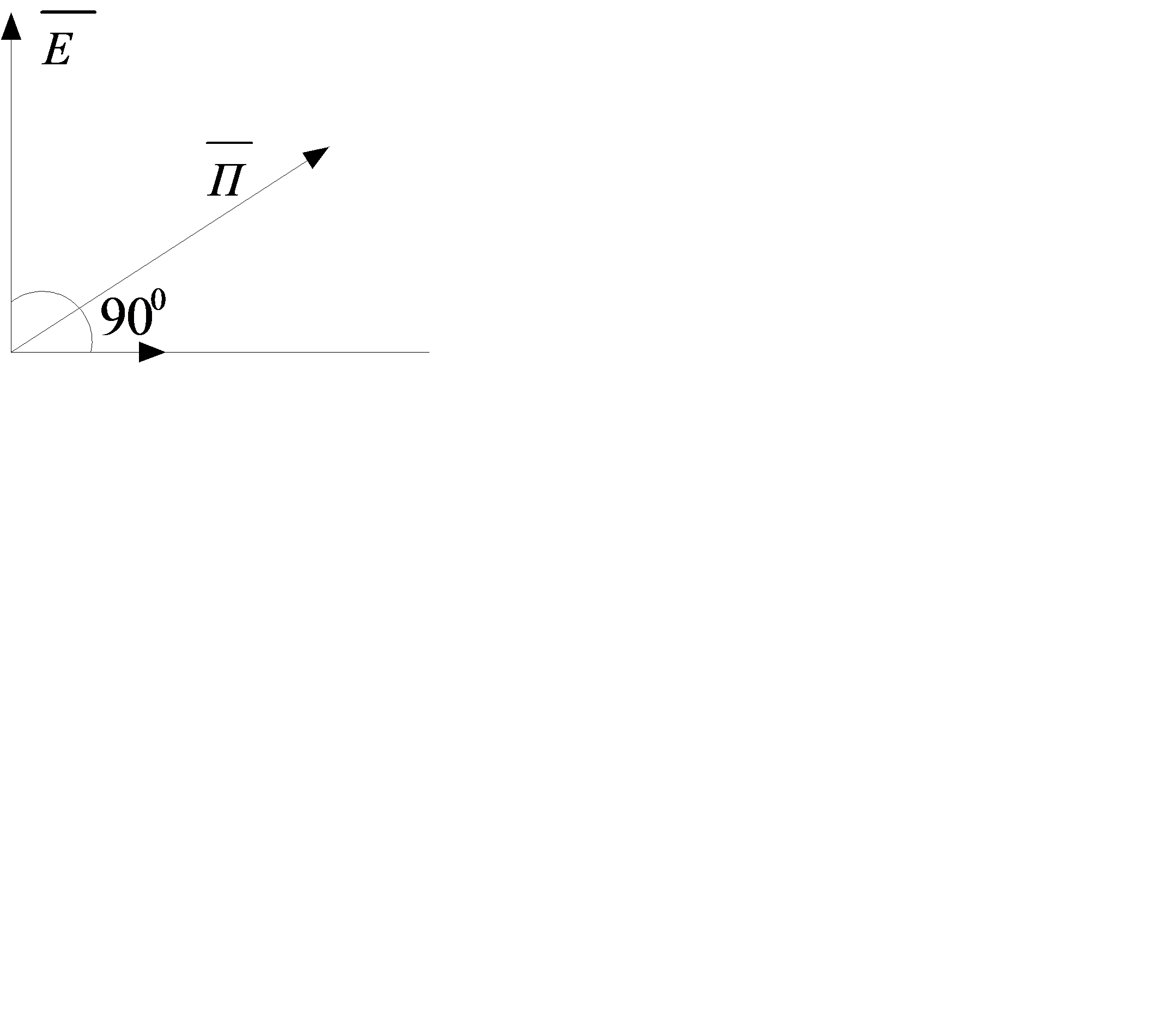 В плоской электромагнитной волне между векторами
В плоской электромагнитной волне между векторами 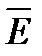 и
и 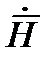 существует пространственный сдвиг в 900.
существует пространственный сдвиг в 900.
Характеристика сред , связывающая абсолютную магнитную проницаемость , удельную проводимость 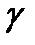 [Сим/м] , угловую чистоту
[Сим/м] , угловую чистоту 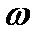 называется волновым сопротивлением проводящей среды
называется волновым сопротивлением проводящей среды
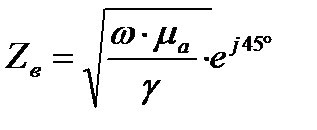 [Ом]
[Ом]
Волновое сопротивление 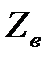 можно трактовать как отношение
можно трактовать как отношение 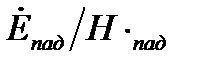 , при этом сдвиг по времени между
, при этом сдвиг по времени между 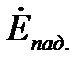 и
и 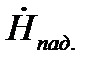 для одной и той же точки поля равен 450 .
для одной и той же точки поля равен 450 .
| <== предыдущая лекция | | | следующая лекция ==> |
| Теоретические основы передачи электромагнитной энергии на расстояние | | | Однотактный усилитель мощности с трансформаторным выходом |
Дата добавления: 2015-12-16; просмотров: 784;
