Теоретические основы передачи электромагнитной энергии на расстояние

Распространение плоской электромагнитной волны в однородном проводящем пространстве.

Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в ней. Так как среда простирается теоретически в бесконечность и подающая волна в толще проводящей среды не встречает границы , которые возмутила бы её распространение , то отраженной волны не возникает .

При наличии только одной падающей волны мгновенные значения Е и Н проводящей среде будут иметь вид

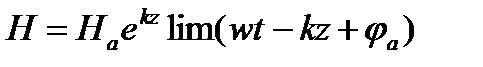(1)

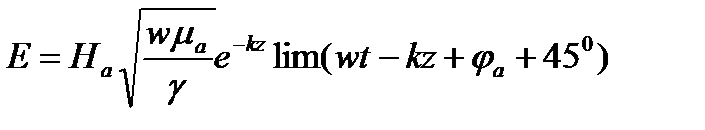(2)

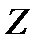
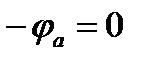
Рис.1 Рис.2

Проанализируем ворожение (1) и (2). Амплитуда

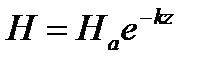
Амплитуда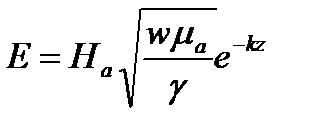

С увеличением z множитель 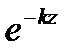уменьшается по показательному закону . Следовательно по мере проникновения электромагнитной волны в проводящую среду амплитуды Е и Н уменьшаются по показательному закону. На рис.1 и 2 изображены огибающее амплитуд Н , построенных на основе 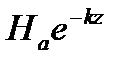. Мгновенное значение Н и Е определяется аргументом синуса .

Кривая (1) на рис.2 получена при 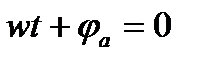. Кривая (2) на рис.2 получена при .

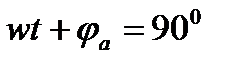Для того , чтобы охарактеризовать на сколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводящую среду , вводиться понятие глубины проникновения .

1. Глубина проникновения и длина волны .

Под глубиной проникновения понимают расстояние вдоль направления распространения волны (вдоль оси z) на котором амплитуда падающей волны Е (или Н) уменьшается в e=2.7 раза.

Отсюда следует, что

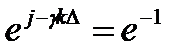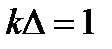или

или

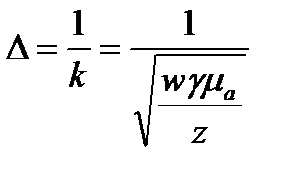
Глубина проникновения обратно пропорциональна корню квадратному от частоты w, проводимости и абсолютной магнитной проницаемости .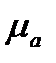

Так при частоте 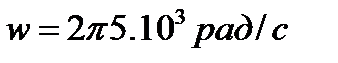или 5 кГц, удельной проводимости 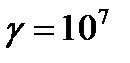, 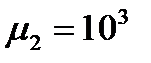глубина проникновения электромагнитной волны будет 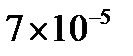или . На этой глубине в амплитуда Е и Н снизится 2.71 раза.

На этом явлении основан эффект снижения электромагнитного излучения от мониторов ПЭВМ за счет нанесения на него (напыления) тонкого слоя металла.

Под длиной волны 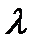в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменится на 2 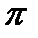. Длину волны определяют из уравнения

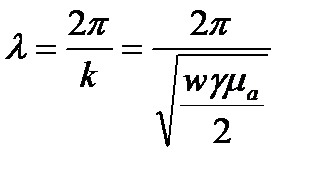
При распространении электромагнитной волны в физической среде используют понятие фазовой скорости.

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу.

Фаза колебания определяется выражением

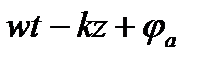(1)

Возьмем первую производную от (1) по времени

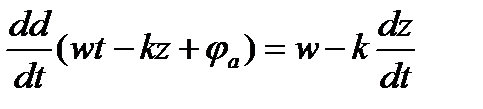т.к.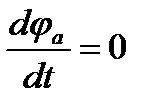

По определению 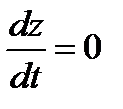, по этому

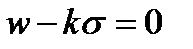
7.Практическое применение явления распространения электромагнитной волны в проводящих телах.

а. Явление затухания электромагнитной волны в поверхностном слое металла используют для экранировки в переменном магнитном поле. Экран выполняет две функции:

- защищает устройство, заключенное в экран от влияния внешнего по отношению к экрану электромагнитного поля;

- защищает внешнее по отношению к экрану пространство от электромагнитного поля создаваемого устройством, заключенным в экране.

Для хорошей экранировки толщина стенки экрана должна быть примерно равна длине волны в металле.

б. Высоко частотный нагрев металлических деталей.

Нагрев металлических деталей перед ковкой и штамповкой, на плавку и реставрацию инструмента часто производят путем помещения этих предметов (деталей) в электромагнитное поле сравнительно не высокой частоты (1-20КГц).

Стальные изделия (валы, шестеренки) подвергают поверхностной закалке, помещая в электромагнитное поле более высокой частоты (до 1МГц) при этом электромагнитная волна, проникая в толщу металла, быстро затухает и отдает свою энергию на нагрев в тонком поверхностном слое стального изделия. Под действием теплоты последней быстро разогревается до температуры, необходимой для поверхностной закалки. Высоко частотные поля не используются для высока качественного нагрева пластмасс перед штамповкой , для термической обработки пищевых продуктов , вулканизации резины и других целей

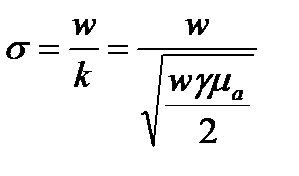
1. Распространение электромагнитных волн в однородном и изотропном диэлектрике .

Проводимость 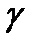идеального диэлектрика равна нулю .

Поэтому в первом уравнении Максвелла 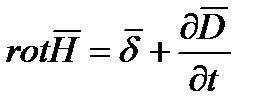; 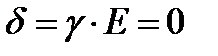и уравнение Максвелла для диэлектрика приобретает вид:

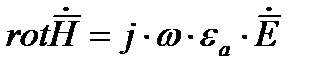
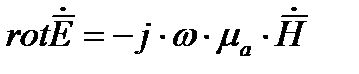
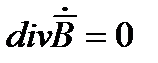
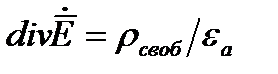
Для однородных и изотропных диэлектриков 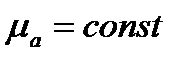и условие 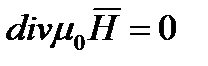равносильно условию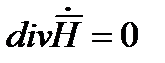

Без вывода для плоской линейно-поляризованной волны , распространяющиеся в направлении оси Z напряженность магнитного поля определяется выражением

;

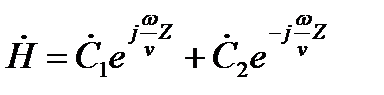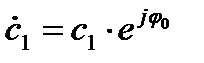
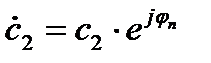
Где 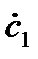и 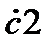-комплексные коэффициенты зависящие от граничных условий

Слагаемое 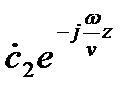- представляет собой падающую волну, продвигающуюся в положительном направлении оси Z.

Слагаемое 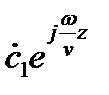- представляет собой отраженную волну, распределяющуюся в отрицательном направлении оси Z.

Напря женность электрического поля для плоской волны расписывается как:

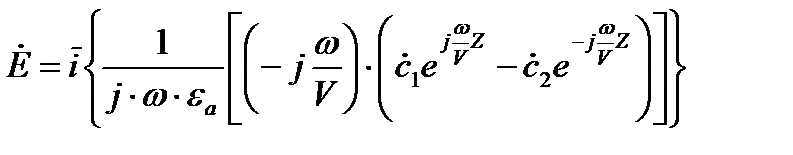
Величину 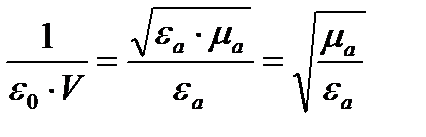- называют волновым сопротивлением диэлектрика.

Волновое сопротивление является чисто действительным числом измеряется в Омах

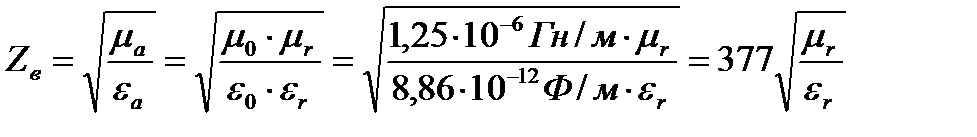
Оно не зависит от угловой частоты колебаний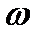

Для вакуума 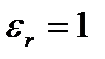и 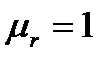, поэтому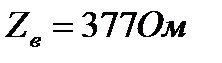

В плоской электромагнитном волне распространяющиеся в диэлектрике как и для проводящей среды 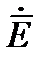и 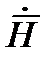взаимно перпендикулярны. 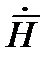направлено на оси У; 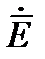- по оси Х.

Под длиной волны 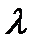в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси Z) на котором среда колебания изменится на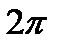

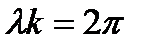,отсюда

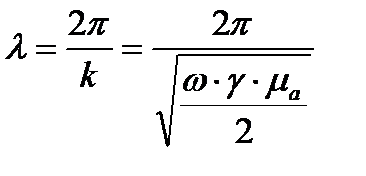[м]При распространении электромагнитной волны в физической среде используют понятие фазовой скорости.

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси Z, чтобы колебание имело одну и ту же фазу.

Фаза колебания определяется выражением: 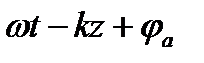(1)

Возьмем первую производную по времени 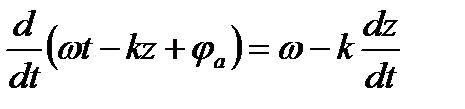т.к.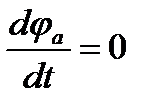

По определению 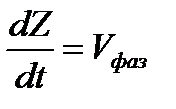, поэтому

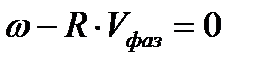
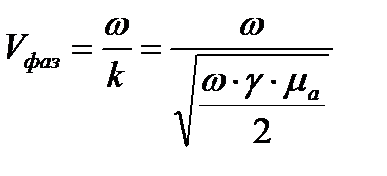[м\с]

Мгновенные значения H и E падающей волны записывается в виде

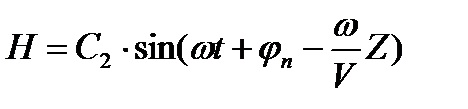_ (1)

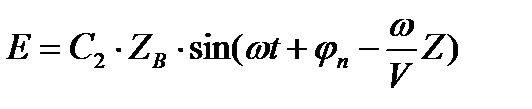(2)

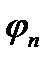- начальная фаза

По мере продвижения падающей волны вдоль оси Z. Амплитуды E и H остаются неизменными, т.е затухания волны не происходит, т.к в диэлектрике нет токов проводимости и нет выделения энергии в виде теплоты. На рис.1 изображении пространственные кривые, представляющие собой графики мгновенных значений H и E. Эти графики построены по уравнениям (1) и (2) для момента времени .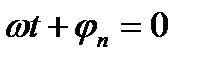

Фазовая скорость электронной волны в диэлектрике:

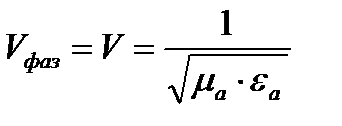
Если волна распространяется в вакууме, то 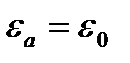и 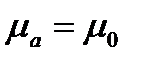и тогда фазовая скорость равна скорости света.

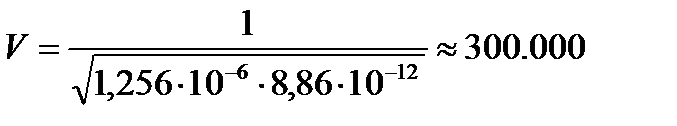км\с

Таким образом фазовая скорость электромагнитной волны в диэлектрике очень велика и несоизмеримо больше фазовой скорости плоской электромагнитной волны в проводящей среде.

Длина волны 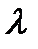есть расстояние вдоль оси Z, на которой фаза колебания изменится на 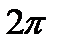. Её находят из соотношения

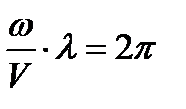, отсюда

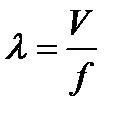
Длина волны в диэлектрике обратно пропорционально частоте. Так длины волны сотового телефона 800Мгц будет равная:

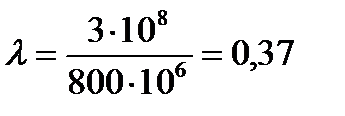[м]