ОСНОВЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ
ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ И ХАРАКТЕРИСТИКИ
В основе гидравлического расчета трубопроводов лежат известные из гидравлики уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности (сплошности) потока для случая несжимаемой жидкости имеет вид
f1 υ 1 f2 υ 2 const, (4)
где f1, f2 — площади 1-го и 2-го сечений трубы;
υ 1, υ 2 — средние скорости движения жидкости в 1-м и 2-м сечениях.
Уравнение (4) показывает, что если в трубопроводе нет притоков и отводов, то расход жидкости в любом сечении является постоянным, а следовательно, средние скорости будут обратно пропорциональны площадям сечений трубы: υ 1/ υ 2 f2/ f1.
Уравнение Бернулли выражает закон сохранения энергии движущейся жидкости. В случае установившегося движения несжимаемой жидкости для 1-го и 2-го сечений потока относительно произвольно выбранной горизонтальной плоскости сравнения оно запишется в следующем виде:
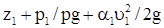
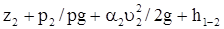 (5)
(5)
где 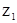 ,
, 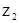 — высоты расположения центров тяжести 1-го и 2-го сечений потока
— высоты расположения центров тяжести 1-го и 2-го сечений потока
над плоскостью сравнения;
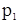 ,
, 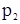 — давления в центрах тяжести 1-го и 2-го сечений;
— давления в центрах тяжести 1-го и 2-го сечений;
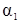 ,
, 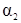 — коэффициенты, учитывающие неравномерность распределения
— коэффициенты, учитывающие неравномерность распределения
скоростей по сечению потока (для турбулентного режима 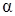 =1,045
=1,045
и практически принимается 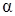 = 1, для ламинарного режима
= 1, для ламинарного режима 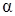 = 2);
= 2);
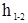 — потерянная удельная энергия потока или потеря напора на участке
— потерянная удельная энергия потока или потеря напора на участке
1—2
Таблица 3
| Температура, °С | Значения V106 при содержании солей по массе | |||
| 0 (пресная вода) | ||||
| 1,789 | 1,804 | 1,815 | 1,825 | |
| 1,516 | 1,530 | 1,544 | 1,556 | |
| 1,306 | 1,320 | 1,334 | 1,348 | |
| 1,145 | 1,152 | 1,165 | 1,179 | |
| 1,007 | 1,019 | 1,032 | 1,045 | |
| 0,897 | 0,905 | 0,917 | 0,930 | |
| 0,805 | 0,816 | 0,827 | 0,838 |
Как известно, ламинарный режим течения наблюдается при числе Рейнольдса Re < 2300, тогда как турбулентный при Re > 2300. Число Рейнольдса Re = υ d/n, где υ — скорость течения жидкости в трубе, м/с; d — внутренний диаметр трубы, м; n — коэффициент кинематической вязкости, м2/с. Для различных капельных жидкостей n зависит главным образом от температуры, уменьшаясь с ее повышением. Значения коэффициента n 106 для воды приведены в табл. 3.
Основным видом течения жидкости в трубопроводах судовых систем является турбулентное. Ламинарный режим течения наблюдается в трубопроводах, транспортирующих жидкости, обладающие значительной вязкостью (мазут, масло, нефть).
По физическому смыслу все члены уравнения (5) представляют собой удельные энергии (отнесенные к единице веса жидкости); так, член z есть удельная потенциальная энергия положения жидкости, член p/pg — удельная потенциальная энергия давления и член 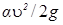 — удельная кинетическая энергия потока в данном сечении. Весь трехчлен z + p/pg+
— удельная кинетическая энергия потока в данном сечении. Весь трехчлен z + p/pg+ 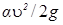 выражает собой полную удельную энергию, которую имеет поток в данном поперечном сечении, т. е. полный гидродинамический напор, выражаемый в метрах столба жидкости. Величина
выражает собой полную удельную энергию, которую имеет поток в данном поперечном сечении, т. е. полный гидродинамический напор, выражаемый в метрах столба жидкости. Величина 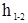 представляет собой уменьшение удельной энергии потока на длине между 1-м и 2-м сечением, затрачиваемой на преодоление сопротивления движению жидкости.
представляет собой уменьшение удельной энергии потока на длине между 1-м и 2-м сечением, затрачиваемой на преодоление сопротивления движению жидкости.
Потери напора h складываются из потерь на трение hт в прямых участках трубопровода и потерь в местных сопротивлениях (задвижке, клапане, колене и др.) hм. Следовательно, можно написать
h = hт + hм. (6)
Потери напора на трение (м) в прямых цилиндрических трубах определяют по формуле Дарси — Вейсбаха
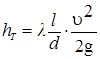 , (7)
, (7)
где 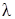 - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
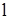 - длина прямой трубы, м;
- длина прямой трубы, м;
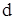 - внутренний диаметр трубы, м;
- внутренний диаметр трубы, м;
υ - средняя скорость жидкости, м/с
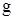 - ускорение свободного падения, м/с2.
- ускорение свободного падения, м/с2.
При определении потерь на трение (м) в трубах прямоугольного сечения используют формулу
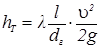 , (8)
, (8)
где dr — гидравлический диаметр, м.
Для прямоугольного канала с размерами сторон а и b гидравлический диаметр
dr = 2аb /( а + b). (9)
Трубы прямоугольного сечения применяют в системах вентиляции и кондиционирования воздуха.
При выполнении расчетов трубопроводов необходимо знать коэффициент гидравлического трения 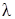 . В общем случае он является функцией числа Рейнольдса Re и шероховатости стенок трубы, по которой протекает жидкость.
. В общем случае он является функцией числа Рейнольдса Re и шероховатости стенок трубы, по которой протекает жидкость.
За меру шероховатости принимают расчетную высоту выступа k, которая называется абсолютной шероховатостью и измеряется в миллиметрах. Для труб промышленного производства, имеющих неравномерное распределение выступов и впадин, волнистость, используют понятие эквивалентной шероховатости kэ. Значение ее получают расчетом, исходя из условия эквивалентности гидравлического сопротивления труб одинаковых длин и внутренних диаметров, одна из которых имеет равномерную зернистую шероховатость, а другая — неравномерную.
Отношение абсолютной шероховатости k(kэ) к характерному линейному поперечному размеру трубы (обычно к диаметру) называется относительной шероховатостью 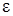 , т. е.
, т. е. 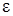 = k/d или
= k/d или 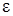 = kэ/d.
= kэ/d.
Для ламинарного режима течения независимо от 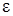 значение
значение 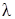 определяют по формуле
определяют по формуле
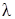 = 64/Re. (10)
= 64/Re. (10)
Для технически гладких трубопроводов, т. е. когда kэ ≈ 0 и 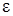 ≈ 0 при Re > 2300
≈ 0 при Re > 2300
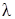 = (1,8 Re – 1,5)-2. (11)
= (1,8 Re – 1,5)-2. (11)
Как частный случай для указанных трубопроводов при 2300 < Re < 105 коэффициент 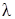 может быть найден по формуле
может быть найден по формуле
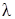 = 0,3164 Re - 0,25 (12)
= 0,3164 Re - 0,25 (12)
Для шероховатых труб при условии, что Re > 2300, т. е. для всей области турбулентного течения, коэффициент 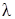 можно определить по формуле
можно определить по формуле
λ=0,1 (1,46 kэ/d+100/Re)0,25. (13)
Эквивалентная шероховатость стальных труб, не бывших в эксплуатации, изменяется в пределах от 0,02 до 0,2 мм в зависимости от технологии их изготовления, срока хранения и т. д.. Для новых алюминиевых труб значение kэ принимают в среднем равным 0,025 мм.
Коэффициент λ можно также найти по графику рис. 20, на котором представлены кривые λ=f(Re,d/kэ). Кривая предельных значений чисел Рейнольдса Reпp показывает, что в области справа от нее коэффициент λ зависит только от относительной шероховатости.
Местные потери напора (м) вычисляют по формуле
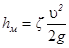 (14)
(14)
где 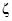 – коэффициент местного сопротивления;
– коэффициент местного сопротивления;
υ – средняя скорость жидкости на входе в местное сопротивление или выходе из него, м/с.
Если на отдельном участке трубопровода имеется несколько местных сопротивлений, то потерю напора на нем определяют как сумму потерь напора в отдельных местных сопротивлениях, т. е.
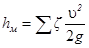 (15)
(15)
Такое суммирование местных сопротивлений справедливо, если они удалены одно от другого на расстоянии 10 диаметров трубы. При меньшем расстоянии
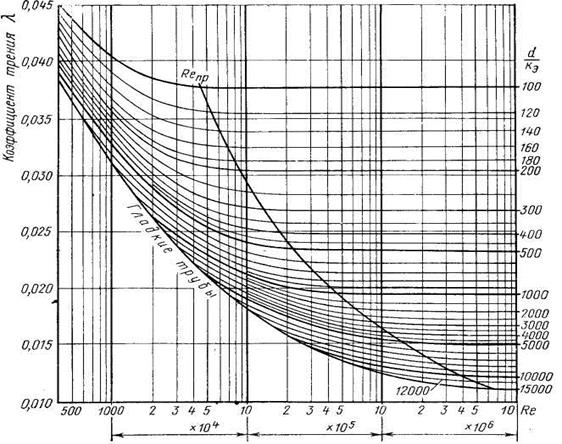
Числа Re
Рис. 20. Зависимость коэффициента гидравлического трения от числа Рейнольдса для стальных труб разного диаметра
между местными сопротивлениями наблюдается их взаимное влияние, выражающееся в увеличении коэффициента 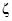 . Однако в практике расчета трубопроводов этим влиянием обычно пренебрегают и расчет ведут по формуле (15).
. Однако в практике расчета трубопроводов этим влиянием обычно пренебрегают и расчет ведут по формуле (15).
Коэффициент местного сопротивления 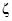 есть величина безразмерная и в общем случае является функцией числа Рейнольдса потока и вида местного сопротивления (крана, клапана, тройника и др.), т. е.
есть величина безразмерная и в общем случае является функцией числа Рейнольдса потока и вида местного сопротивления (крана, клапана, тройника и др.), т. е. 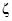 = f (Re, вид местного сопротивления).Несмотря на наличие большого количества экспериментальных материалов и теоретических исследований, общие зависимости для
= f (Re, вид местного сопротивления).Несмотря на наличие большого количества экспериментальных материалов и теоретических исследований, общие зависимости для 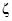 , относящиеся ко всем видам местных сопротивлений, еще не получены.
, относящиеся ко всем видам местных сопротивлений, еще не получены.
Для некоторых наиболее простых видов местных сопротивлений (резкое расширение, течение жидкости в конических трубах, диафрагмы и др.) получены теоретические формулы, по которым определяют потери напора в них. В большинстве случаев 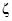 находят экспериментальным путем. При выборе коэффициента местного сопротивления в первую очередь следует учитывать режим движения потока, т. е. значение Re потока, при котором были получены значения
находят экспериментальным путем. При выборе коэффициента местного сопротивления в первую очередь следует учитывать режим движения потока, т. е. значение Re потока, при котором были получены значения 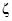 , пределы применимости опытных данных, а также, к какой скорости препятствий они отнесены. Практически при Re ≥ 105 изменением коэффициента
, пределы применимости опытных данных, а также, к какой скорости препятствий они отнесены. Практически при Re ≥ 105 изменением коэффициента 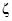 можно пренебречь и считать, что он является величиной постоянной. Значения коэффициентов
можно пренебречь и считать, что он является величиной постоянной. Значения коэффициентов 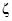 , представляют либо в табличной форме, либо в виде графиков или в виде экспериментальной формулы.
, представляют либо в табличной форме, либо в виде графиков или в виде экспериментальной формулы.
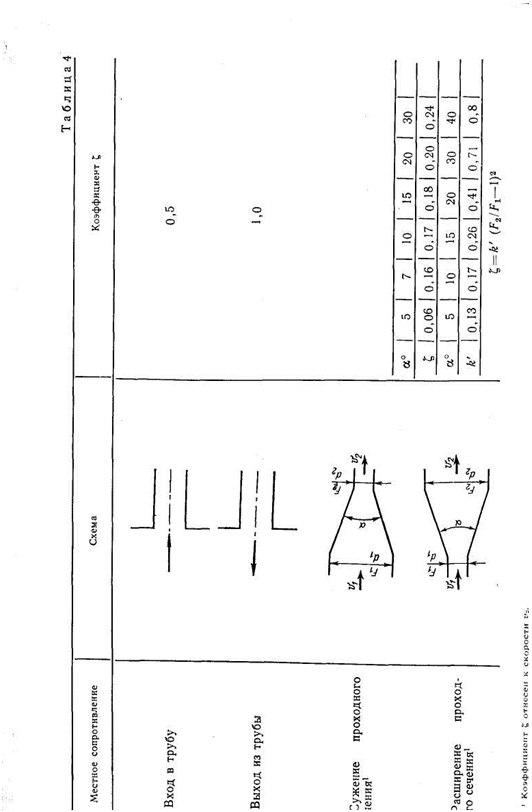
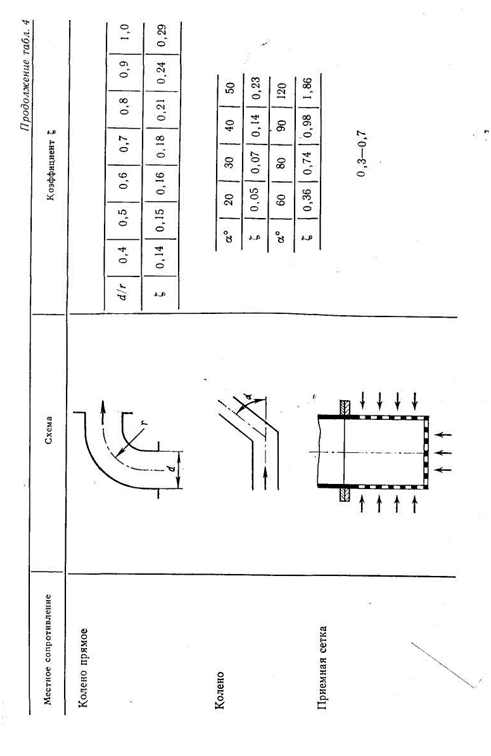
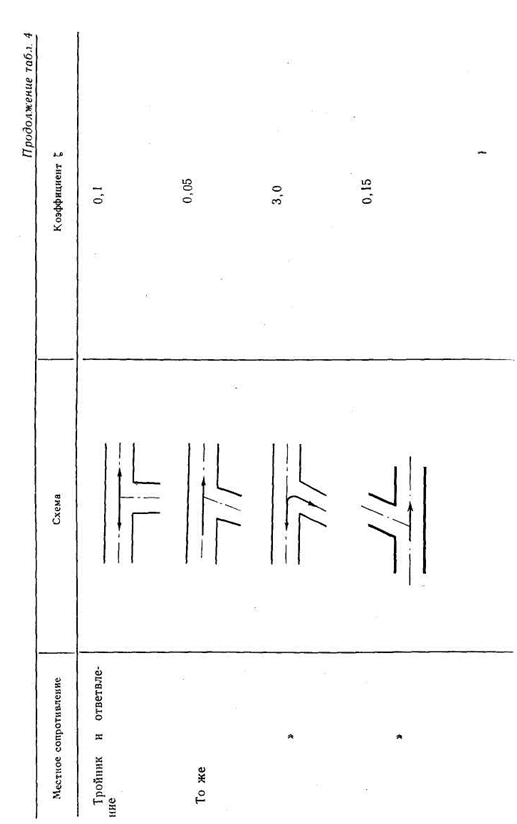
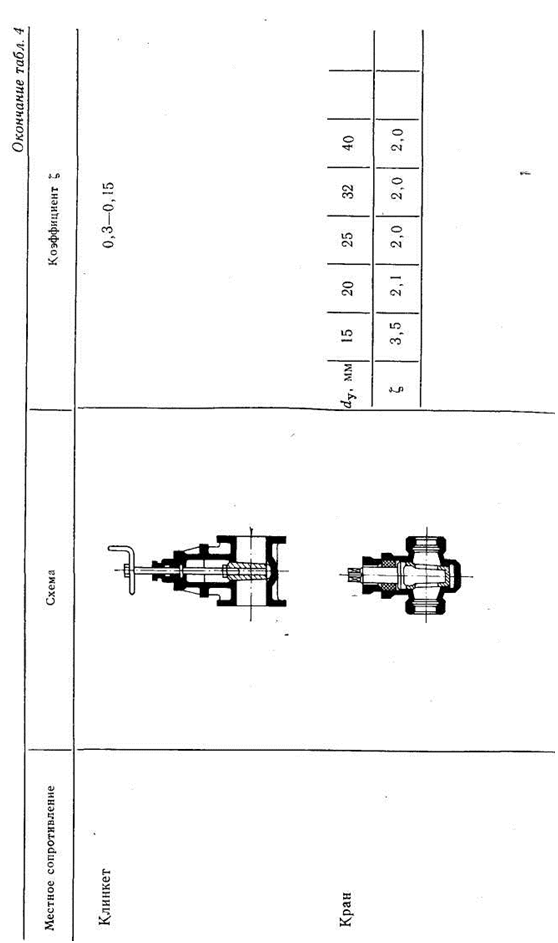
В табл. 4 приведены значения коэффициентов местных сопротивлений 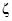 для некоторых элементов судовых водопроводов. Подробные сведения по различным видам гидравлических сопротивлений содержатся в справочной итературе. Значения коэффициентов сопротивления
для некоторых элементов судовых водопроводов. Подробные сведения по различным видам гидравлических сопротивлений содержатся в справочной итературе. Значения коэффициентов сопротивления 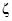 арматуры часто указывают на чертежах завода — поставщика арматуры.
арматуры часто указывают на чертежах завода — поставщика арматуры.
Выведем формулу для построения характеристики трубопровода. Потери напора в трубопроводе можно выразить зависимостью
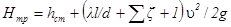 ,
,
где 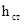 — статическая высота подачи, равная сумме геометрической и манометрической высот, причем под последней подразумевается высота, соответствующая избыточному давлению в системе (пневмоцистерне, магистрали водотушения и др.); 1 — учитывает потерю с выходной скоростью в случае концевой трубы.
— статическая высота подачи, равная сумме геометрической и манометрической высот, причем под последней подразумевается высота, соответствующая избыточному давлению в системе (пневмоцистерне, магистрали водотушения и др.); 1 — учитывает потерю с выходной скоростью в случае концевой трубы.
Так как при расходе Qтр через трубопровод скорость
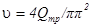 , то
, то 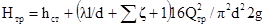
Для каждого данного трубопровода величина 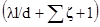
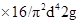 является постоянной. Окончательно получим
является постоянной. Окончательно получим
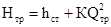 . (16)
. (16)
Это и есть уравнение характеристики трубопровода.
На рис. 21 характеристика трубопровода изображена кривой 2. Если на эту характеристику нанести характеристику насоса 1, то можно определить его режим работы. Точка А пересечения характеристик насоса и трубопровода называется рабочей точкой. Она показывает, что
 |
 |
 |
 |
насос, работая на данный трубопровод, будет обеспечивать подачу Q1, и напор Н1. Изменение характеристики трубопровода вызывает перемещение точки А на характеристике насоса и, следовательно, изменение режима работы последнего.
Характеристику Н— Q насоса строят по результатам испытаний его на стенде при постоянной частоте вращения n (мин-1). Такие характеристики приводятся в каталогах на насосы.
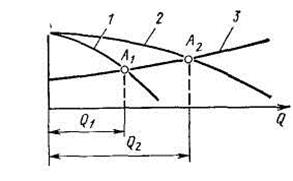
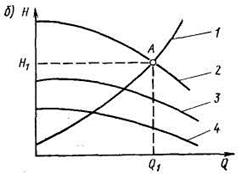
Представим теперь, что в трубопровод жидкость подается не одним, а двумя насосами, подключенными к нему параллельно. При параллельном соединении обеспечивается увеличенная подача жидкости в трубопровод. Будем считать, что насосы одинаковые и характеристика Н— Q каждого из них изображается кривой 1 (рис. 22, а). Суммарная характеристика 2 двух параллельно работающих насосов получается сложением их подач при одинаковых напорах. Нанося на эти характеристики характеристику трубопровода 3, получим рабочие точки А1 и А2, которые определяют количество жидкости, перекачиваемое по трубопроводу од ним (подача Q1) и двумя (подача Q2) параллельно работающими насосами.
На практике встречаются случаи, когда насосы работают последовательно. При последовательном соединении повышается напор насосной установки (рис. 22, б). На рисунке кривая 4 — характеристика одного насоса, а кривая 3—характеристика другого. Суммарная характеристика 2 двух последовательно работающих насосов получается сложением их напоров при одинаковой подаче. Пересечение характеристики 2 насосов с характеристикой 1 трубопровода в точке А определяет режим работы двух последовательно включенных насосов. Последовательное соединение насосов применяют на танкерах при выкачке вязкого нефтегруза на некоторые нефтебазы, расположенные на значительном расстоянии от причала. Форма характеристик Н— Q , изображенных на рис. 21 и 22, свойственна лопастным насосам.
 n= const n= const
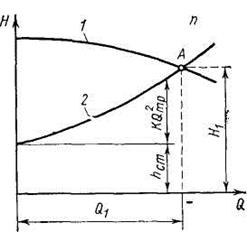 Рис. 21. К определению рабочего
режима насоса
Рис. 21. К определению рабочего
режима насоса
| а)
| |||
| Рис. 22. Графики совместной работы насосов | ||||
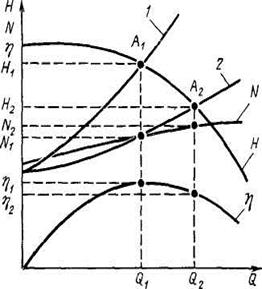 Рис. 23. К определению показателей
работы насоса
Рис. 23. К определению показателей
работы насоса
| У поршневого насоса подача весьма мало зависит от создаваемого им напора, т. е. насос имеет жесткую характеристику. Незначительное уменьшение подачи поршневого насоса с увеличением напора объясняется возрастанием протечек жидкости внутри насоса. На практике этим уменьшением подачи обычно пренебрегают и характеристику Н— Q поршневого насоса изображают в виде прямой, параллельной оси ординат. Для суждения об экономичности работы лопастного насоса в системе на характеристику трубопровода наносят характеристики Н— Q, Н— Q и η — Q насоса (рис.23). Пользуясь такими | |||
| характеристиками, можно при каждой данной подаче Q определить не только необходимый напор Н насоса, но также его мощность N и к. п. д. η. Так, например, рабочей точке А1 соответствует подача Q1 напор Н1 мощность N1 и к. п. д. η1; рабочей точке А2— Q2, Н2, N2 и η2 . Как видно, на трубопровод 1 насос будет работать более экономично, чем на трубопровод 2, поскольку η1 > η2 . При подборе насоса для судовой системы стремятся к тому, чтобы он на расчетном режиме имел максимальный к. п. д. | ||||
Дата добавления: 2015-12-11; просмотров: 3692;
