АНАЛИТИЧЕСКИЙ МЕТОД. Данный метод основан непосредственно на решении двух уравне­ий: уравнения Бернулли и уравнения расхода

Данный метод основан непосредственно на решении двух уравне­ий: уравнения Бернулли и уравнения расхода. Этим методом рассчитывают как простые, так и сложные (разветвленные) трубопроводы.

Расчет простого трубопровода. В расчетной схеме сеть трубопрово­дов системы обычно разбивают на отдельные участки, в пределах ко­торых сохраняются постоянство расхода жидкости и постоянство диа­метра сечения трубы. Такие трубопроводы называют простыми.

Рассмотрим расчет простого трубопровода (см. рис. 17). Напишем уравнение Бернулли для сечений 1 и 2 трубопровода:

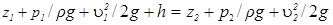(17)

Входящая в уравнение величина h, представляющая собой потери на трение и местные сопротивления, определяется зависимостью

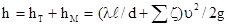(18)

Подставив в уравнение (17) значение h по формуле (18) и решив его относительно p₂/rg, получим напор H₂ в узловой точке 2:

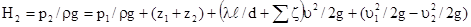(19)

Так как диаметр трубопровода постоянный, то 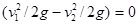и уравнение (19) примет окончательный вид

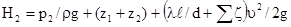
Представим зависимость (24) в виде

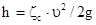(20)

где 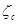— суммарный (полный) коэффициент сопротивления трубопровода сис­темы, определяемый по формуле

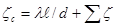(21)

Поскольку в основной расчётной формуле (20) потери напора выражены в функции скоростного напора, то рассматриваемый метод расчёта часто называют методом динамических напоров.

Из формулы (20) получим выражение для скорости движения жидкости в трубопроводе

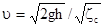
Расход жидкости в трубопроводе будет равен расходу жидкости у потребителя в точке 1. Для большинства потребителей (пожарного ствола, водораспылителя, дренчера и др.)

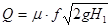(22)

где 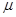— коэффициент расхода;

f — площадь сечения отверстия истечения у потребителя, м²;

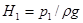— напор у потребителя, м.

Зная расход Q, можно найти диаметр трубопровода по формуле

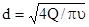(23)

Покажем, как используют формулы при расчете трубопроводов. Если напор H₂ в узловой точке 2 (см. рис. 24) является искомой величи­ной, то расчет трубопровода выполняют в такой последовательности: исходя из заданного напора Н₁ у потребителя определяют расход Q жидкости по формуле (22); задавшись скоростью движения жидкости в трубопроводе, вычисляют его диаметр d по формуле (23); подбирают условный проход трубы, а затем находят по соответствующему госу­дарственному стандарту фактические наружный и внутренний диамет­ры трубы; уточняют скорость движения жидкости в трубе по формуле υ 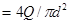; вычисляют число Рейнольдса 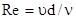; по найденному значению Re и принятому значению эквивалентной шероховатости k_э вычисляют коэффициент гидравлического трения l или находят его по графику рис. 20; пользуясь табл. 4 или другими источниками, опреде­ляют сумму коэффициентов местных сопротивлений 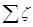; вычисляют суммарный коэффициент сопротивлений 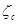по формуле (21); определяют потери напора h в трубопроводе по формуле (20); находят напор в уз­ловой точке 2 по выражению H₂=H₁+h+(z₁-z₂). Из данного расчета видно, что задача решается полностью и в конечном виде.

Рассмотрим случай гидравлического расчета того же трубопровода 1—2, когда напор H₂ в узловой точке 2 является заданным. Цель рас­чета — определить скорость υ жидкости в трубопроводе, а также рас­ход Q и напор H₁ ее у потребителя. Диаметр d трубопровода предвари­тельно назначают. Данная задача решается рядом последовательных приближений. Задаемся в 1-м приближении напором у потребителя H₁=H₁^’ и вычисляем следующие величины:

расход воды на участке

;

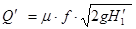скорость движения жидкости в трубопроводе

;

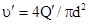число Рейнольдса

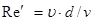
суммарный коэффициент сопротивления трубопровода

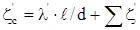
потери напора в трубопроводе

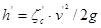
Далее решаем задачу во 2-м приближении. Напор у потребителя будет равен

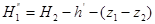
Повторяем расчет по тем же формулам и в такой же последователь­ности, как и в 1-м приближении. В результате получаем 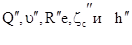. И так делаем ряд последовательных приближений, пока не получим значения напора 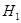для всех двух последующих приближе­ний, близкие между собой.

Расчет сложного трубопровода. Любой сложный (разветвленный) трубопровод состоит из отдельных простых трубопроводов, соединен­ных по определенной схеме. Гидравлический расчет разветвленного трубопровода (см. рис. 25) выполняется по участкам и обычно сводится к применению для них решений, рассмотренных для простых трубо­проводов. Как видно из рис. 25, насос по разветвленному трубопроводу подает воду к целому ряду потребителей. В данной схеме число потре­бителей равно четырем; в общем случае их может быть значительно больше. Предположим, что напор H и подача Q насоса неизвестны. Расчет трубопровода производим последовательно по участкам от са­мой отдаленной точки 1 к насосу (рис. 25, а). Участок 1—2 представля­ет собой простой трубопровод и рассчитывается в таком порядке:

расход воды на участке

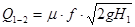
диаметр трубопровода

,

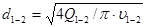где 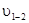— скорость жидкости в трубопроводе, которой задаются в предела 2-4 м/с,

число Рейнольдса

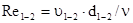
суммарный коэффициент сопротивления трубопровода

;

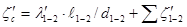потери напора на участке

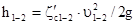
напор в точке 2

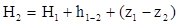
Участок 2—3 также представляет собой простой трубопровод, и по­скольку для него напор в точке 2 тот же, что и для участка 1-2 , т.е. H₂ то рассчитывают его рядом последовательных приближений.

Участок 2—4 — простой трубопровод и рассчитывается следующим образом. Определяют расход воды на участке Q_2-4=Q_1-2+Q_2-3, а затем вычисляют d_2-1, Re_2-4, z_c2-4, h_2-4 и находят напор H₄ в точ­ке 4 по формуле

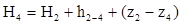
После этого рассчитывают участки 4—5, 4—6, 6—7 и 6—8.

Подача и напор насоса системы будут равны: Q=Q_6-8, H=H₈

В общем случае потребную подачу насоса определяют по выраже­нию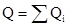

где 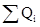— сумма расходов воды потребителями, рабо­тающими одновременно.

Из всех возможных комбинаций одновременной работы потребите­лей берут тот случай, когда расход воды будет максимальным.

Если подача Q и напор H насоса заданы, то целью расчета является определение параметров движения жидкости по участкам, а также на­пора и расхода жидкости у потребителей. На участки трубопровод раз­бивают в направлении от насоса к самой удаленной точке (рис. 25, б). Расчет начинают с магистрали 1- 4, а затем рассчитывают отдельные ответвления. Приняв скорость υ_м движения жидкости в магистрали рав­ной 2-4 м/с, определяют ее диаметр по формуле

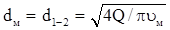
Участки магистрали рассчитывают последовательно один за дру­гим, начиная с участка 1—2. Для этого участка имеем:

число Рейнольдса

;

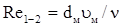потери напора

;

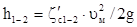напор в точке 2

.

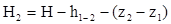Аналогично рассчитывают участки 2—3 и 3—4.

Напор в точке 3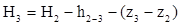

Напор в точке 4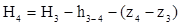

По известным напорам в узловых точках 2,3 и 4 рассчитывают от­ветвления 2—6, 3—7, 4—8 и 4—5.