Рекомендации к решению заданий 8 – 14.

Пример 1. Найти векторное произведение векторов 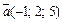и .

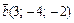Решение. Составим и вычислим определитель:

.

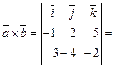
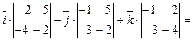
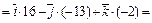
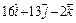Таким образом, векторное произведение векторов 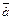и 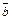есть вектор: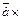 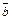= = 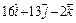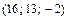. Ответ: .

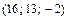Пример 2. Найти площадь параллелограмма, построенного на векторах 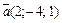и .

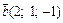Решение. Найдем векторное произведение векторов 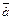и :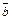

= .

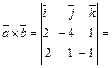
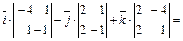
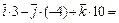
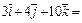
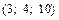Тогда площадь параллелограмма, построенного на векторах 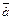и 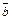, равна модулю векторного произведения:

S_пар .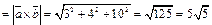

Ответ: .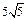

Пример 3. Вычислить модуль векторного произведения векторов 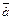и 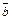, если .

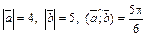Решение. Модуль векторного произведения векторов 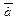и 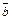равен:

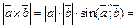
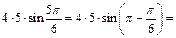
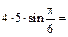
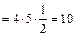. Ответ: 10.

Пример 4. Найти площадь треугольника, построенного на векторах 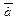и 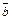, если .

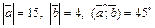Решение.

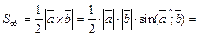
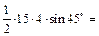
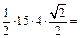
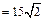. Ответ: .

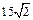Пример 5. Найти смешанное произведение векторов .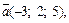

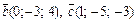Решение. Смешанное произведение векторов, заданных коорди­натами, равно:

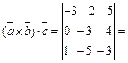
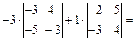
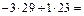
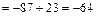. Ответ: –64.

Пример 6. Проверить, что векторы 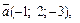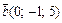, 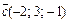компланарны.

Решение. Найдем смешанное произведение данных векторов:

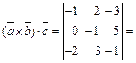
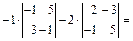
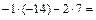
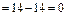. Так как смешанное произведение векторов равно 0, значит векторы 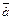, , 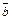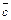компланарны.

Пример 7. Найти объем пирамиды АВСD с вершинами , , , .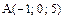

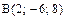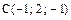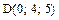Решение. Найдем векторы, образующие пирамиду:

;

.

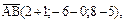
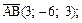
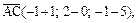
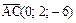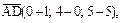
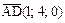Тогда объем пирамиды АВСD равен 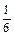смешанного произведения этих векторов, взятого по абсолютной величине. Найдем смешанное произведение векторов:

.

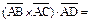
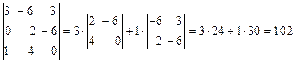Объем пирамиды АВСD равен 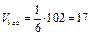. Ответ: 17.