Рекомендации к решению заданий 5 – 7. 1 страница
Пример 1. Найти скалярное произведение векторов 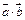 , если
, если 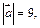
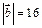 ,
, 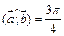 .
.
Решение. Применим формулу 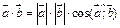 . Тогда скалярное произведение векторов
. Тогда скалярное произведение векторов 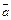 и
и 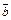 равно:
равно: 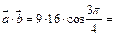
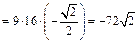 . Ответ: –
. Ответ: – 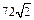 .
.
Пример 2. Найти угол, образованный векторами 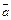 и
и 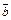 , если
, если 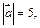
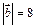 ,
, 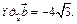
Решение.
1-й способ. Из формулы 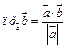 находим скалярное произведение векторов
находим скалярное произведение векторов 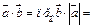
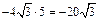 . Угол между векторами
. Угол между векторами 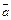 и
и 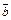 найдем по формуле
найдем по формуле 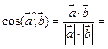
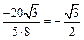 . Значит угол между векторами
. Значит угол между векторами  и
и  равен
равен 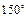 .
.
2-й способ. Для данных условий угол между векторами 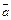 и
и 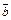 найдем следующим образом:
найдем следующим образом: 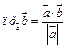 =
= 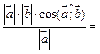
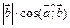 , отсюда
, отсюда 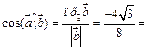
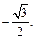 Ответ:
Ответ: 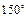 .
.
Пример 3. Найти проекцию вектора 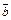 на вектор
на вектор 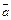 , если
, если 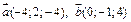 .
.
Решение. Применим формулу 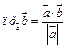 . Найдем скалярное произведение векторов
. Найдем скалярное произведение векторов 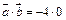
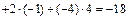 и длину вектора
и длину вектора 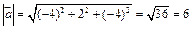 . Тогда
. Тогда 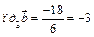 .
.
Ответ: – 3.
Пример 4. Вычислить работу, произведенную силой 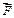 по перемещению тела из точки С в точку В, если
по перемещению тела из точки С в точку В, если 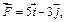
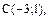
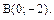
Решение. Работа, произведенная силой 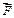 по перемещению тела из точки С в точку В, равна скалярному произведению векторов силы
по перемещению тела из точки С в точку В, равна скалярному произведению векторов силы 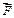 и перемещения
и перемещения 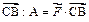 . Вектор перемещения имеет координаты
. Вектор перемещения имеет координаты 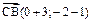 , или
, или 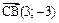 . Тогда работа силы
. Тогда работа силы 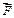 равна
равна 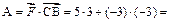
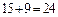 . Ответ: 24.
. Ответ: 24.
Задание 8.Найти векторное произведение векторов 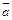 и
и 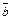 .
.
Задание оценивается в 1 балл.
| Номер задания | Исходные данные | Варианты ответов | |||
| 8.1 | 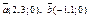
| 1) (–2; 3; 0) | 2) (0; 0; 5) | 3)(1; 4; 0) | 4)(1; 1; 4) |
| 8.2 | 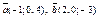
| 1)(–2; 0; 1) | 2)(1; 0; 1) | 3) (0; 5; 0) | 4)(1; 0; –12) |
| 8.3 | 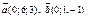
| 1)(0; 6; –3) | 2) (–9; 0; 0) | 3)(0; 7; 2) | 4)(0; 6; 2) |
| 8.4 | 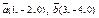
| 1) (0; 0; 2) | 2)(4; –6; 0) | 3)(3; 6; 0) | 4)(2; –2; 0) |
| 8.5 | 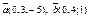
| 1)(0; 7; 4) | 2)(0; 12; –4) | 3)(2; 0; 0) | 4) (23; 0; 0) |
| 8.6 | 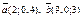
| 1)(18; 0; 12) | 2)(11; 0; 7) | 3) (0; 30; 0) | 4)(0; 28; 0) |
| 8.7 | 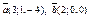
| 1) (0;–8; –2) | 2)(5; 1; –4) | 3)(6; 1; 0) | 4)(0; –7; 1) |
| 8.8 | 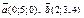
| 1) (0; 15; 0) | 2) (20;0;–10) | 3)(2; 8; 4) | 4)(10; 0; –5) |
| 8.9 | 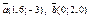
| 1)(1; 8; –3) | 2)(4; 0; 5) | 3) (6; 0; 2) | 4)(0; 12; 0) |
| 8.10 | 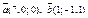
| 1) (0;–7;–7) | 2)(0; 1; 5) | 3)(7; 0; 0) | 4)(8; –1; 1) |
| 8.11 | 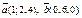
| 1)(1; 8; 4) | 2)(0; 12; 0) | 3)(–20; 0; 5) | 4) (–24;0;6) |
| 8.12 | 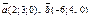
| 1) (0;0;26) | 2)(–12; 1; 0) | 3)(–4; 7; 0) | 4)(0; 0; 6) |
| 8.13 | 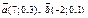
| 1)(–14; 0; 3) | 2) (0;–13;0) | 3)(5; 0; 4) | 4)(0; –10; 5) |
| 8.14 | 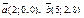
| 1)(10; 0; 0) | 2)(7; 2; 8) | 3) (0;–16;4) | 4)(0; –17; 5) |
| 8.15 | 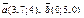
| 1)(3; 12; 4) | 2)(0; 35; 0) | 3)(–10; 0; 5) | 4) (–20;0;15) |
| 8.16 | 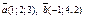
| 1)(–1; 6; 6) | 2) (–8;–5; 6) | 3)(0; 6; 5) | 4)(–4; –1; 5) |
| 8.17 | 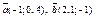
| 1) (–4; 7; –1) | 2)(1; 1; 3) | 3)(–2; 0; –4) | 4)(–2; 4; 5) |
| 8.18 | 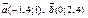
| 1)(0; 8; 4) | 2)(–1; 8; 4) | 3)(10; 4; –6) | 4) (14;4; –2) |
| 8.19 | 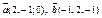
| 1)(–2; –2; 0) | 2) (1; 2; 5) | 3)(1; 1; –1) | 4)(1; 2; 3) |
| 8.20 | 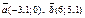
| 1)(–18; 5; 0) | 2)(3; 6; 0) | 3) (1; 3; –21) | 4)(2; –9; 5) |
| 8.21 | 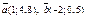
| 1)(1; 4; 13) | 2)(–2; 0; 40) | 3) (20;–21;8) | 4)(10; 11; 5) |
| 8.22 | 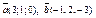
| 1)(2; 3; –3) | 2) (–3; 9; 7) | 3)(5; 1; 9) | 4)(–3; 3; –3) |
О к о н ч а н и е
| 8.23 | 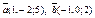
| 1)(–4;–7;–2) | 2)(0; –2; 7) | 3)(–1; –2; 1) | 4)(1; 6; 5) |
| 8.24 | 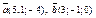
| 1)(8; 0; –4) | 2)(15; –1; 0) | 3)(–5; 10; 1) | 4) (–4;–12;–8) |
| 8.25 | 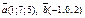
| 1)(0; 7; 7) | 2)(–1; 0; 10) | 3)(10; –5; 5) | 4) (14;–7;7) |
| 8.26 | 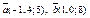
| 1) (32;13;–4) | 2)(0; 0; 40) | 3)(30; 15; 5) | 4)(0; 4; 13) |
| 8.27 | 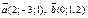
| 1)(2; –2; 3) | 2) (–7;–4;2) | 3)(0; –3; 2) | 4)(–5; –3; 5) |
| 8.28 | 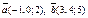
| 1)(–3; 0; 10) | 2)(2; 4; 7) | 3) (–8;11;–4) | 4)(–7; 1; –3) |
| 8.29 | 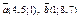
| 1)(5; 13; 8) | 2)(4; 40; 8) | 3)(17; 17;17) | 4)(27;–27;27) |
| 8.30 | 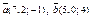
| 1) (8;–33;–10) | 2)(35; 0; –4) | 3)(12; 0; –4) | 4)(8; –30; 5) |
Задание 9.Найти площадь параллелограмма, построенного на векторах 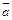 и
и 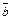 , как на сторонах.
, как на сторонах.
Задание оценивается в 1 балл.
| Номер задания | Исходные данные | Варианты ответов | |||
| 9.1 | 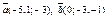
| 1) 1 | 2) 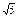
| 3) 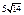
| 4) 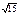
|
| 9.2 | 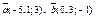
| 1) 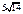
| 2) 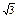
| 3) 1 | 4) 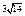
|
| 9.3 | 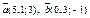
| 1) 1 | 2) 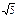
| 3) 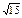
| 4) 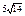
|
| 9.4 | 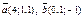
| 1) 7 | 2) 6 | 3) 5 | 4) 4 |
| 9.5 | 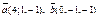
| 1) 4 | 2) 5 | 3) 6 | 4) 7 |
| 9.6 | 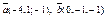
| 1) 6 | 2) 5 | 3) 4 | 4) 3 |
| 9.7 | 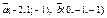
| 1) 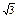
| 2) 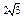
| 3) 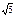
| 4) 2 |
| 9.8 | 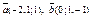
| 1) 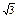
| 2) 2 | 3) 1 | 4) 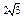
|
| 9.9 | 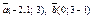
| 1) 2 | 2) 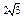
| 3) 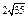
| 4) 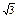
|
| 9.10 | 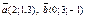
| 1) 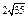
| 2) 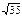
| 3) 2 | 4) 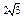
|
| 9.11 | 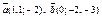
| 1) 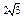
| 2) 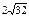
| 3) 2 | 4) 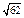
|
| 9.12 | 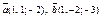
| 1) 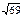
| 2) 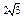
| 3) 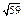
| 4) 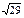
|
| 9.13 | 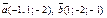
| 1) 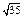
| 2) 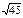
| 3) 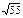
| 4) 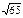
|
| 9.14 | 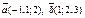
| 1) 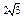
| 2) 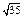
| 3) 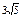
| 4) 8 |
| 9.15 | 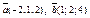
| 1) 5 | 2) 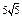
| 3) 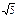
| 4) 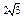
|
| 9.16 | 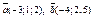
| 1) 6 | 2) 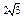
| 3) 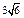
| 4) 9 |
| 9.17 | 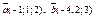
| 1) 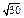
| 2) 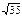
| 3) 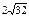
| 4) 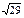
|
| 9.18 | 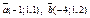
| 1) 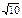
| 2) 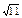
| 3) 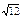
| 4) 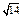
|
О к о н ч а н и е
| 9.19 | 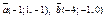
| 1) 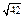
| 2) 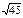
| 3) 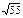
| 4) 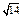
| |||
| 9.20 | 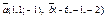
| 1) 7 | 2) 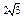
| 3) 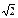
| 4) 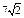
| |||
| 9.21 | 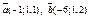
| 1) 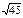
| 2) 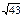
| 3) 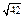
| 4) 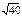
| |||
| 9.22 | 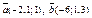
| 1) 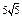
| 2) 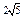
| 3) 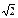
| 4) 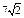
| |||
| 9.23 | 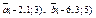
| 1) 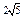
| 2) 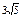
| 3) 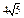
| 4) 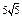
| |||
| 9.24 | 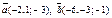
| 1) 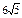
| 2) 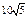
| 3) 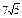
| 4) 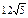
| |||
| 9.25 | 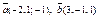
| 1) 2 | 2) 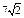
| 3) 
| 4) 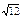
| |||
| 9.26 | 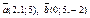
| 1) 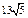
| 2) 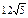
| 3) 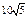
| 4) 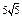
| |||
| 9.27 | 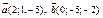
| 1) 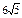
| 2) 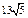
| 3) 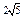
| 4) 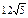
| |||
| 9.28 | 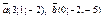
| 1) 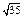
| 2) 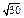
| 3) 3 | 4) 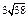
| |||
| 9.29 | 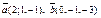
| 1) 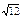
| 2) 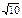
| 3) 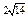
| 4) 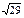
| |||
| 9.30 | 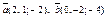
| 1) 10 | 2) 12 | 3) 14 | 4) 15 | |||
Задание 10.Ответить на вопрос задания, выбрав один из вариантов ответов.
Задание оценивается в 1 балл.
| Номер задания | Вопрос задания | Варианты ответов | |||
| 10.1 | Вычислить 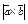 , если , если 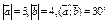
| 1) | 2)
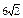
| 3) | 4)
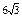
|
| 10.2 | Вычислить 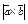 , если , если 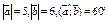
| 1) | 2)
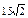
| 3) | 4)
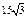
|
| 10.3 | Вычислить 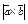 , если , если 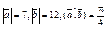
| 1)
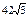
| 2)
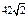
| 3) | 4) |
| 10.4 | Вычислить 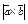 , если , если 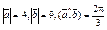
| 1)
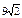
| 2) | 3)
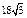
| 4) |
| 10.5 | Вычислить 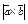 , если , если 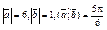
| 1) | 2)
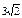
| 3)
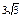
| 4) |
| 10.6 | Вычислить 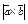 , если , если 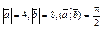
| 1) | 2) | 3) | 4) |
| 10.7 | Вычислить 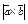 , если , если 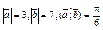
| 1)
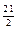
| 2) | 3)
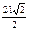
| 4)
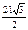
|
| 10.8 | Вычислить 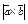 , если , если 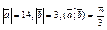
| 1)
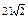
| 2)
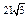
| 3) | 4) |
П р о д о л ж е н и е
Дата добавления: 2015-12-11; просмотров: 711;
