Для самостоятельной работы студентов 4 страница
О к о н ч а н и е
| 3.22 | Записать координаты вектора 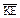 , если K(2; 4; 3),O(4; 2; 5), а точка E является серединой отрезка KO , если K(2; 4; 3),O(4; 2; 5), а точка E является серединой отрезка KO
| 1)

| 2)
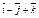
| 3)
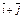
| 4)
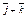
|
| 3.23 | Записать координаты вектора 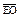 , если А(2; –1; 3), O(2;–3; 5), а точка E является серединой отрезка АO , если А(2; –1; 3), O(2;–3; 5), а точка E является серединой отрезка АO
| 1)
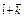
| 2)
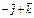
| 3)

| 4)
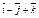
|
| 3.24 | Записать координаты вектора 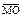 , если М(2; 3; 4), В(4; 5; 2), а точка В является серединой отрезка МO , если М(2; 3; 4), В(4; 5; 2), а точка В является серединой отрезка МO
| 1)
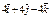
| 2)
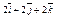
| 3)
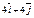
| 4)

|
| 3.25 | Записать координаты вектора 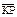 , если К(2; –1; –3), О(4; –3; 5), а точка Р является серединой отрезка КO , если К(2; –1; –3), О(4; –3; 5), а точка Р является серединой отрезка КO
| 1)
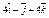
| 2)
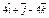
| 3)
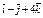
| 4)

|
| 3.26 | Записать координаты вектора 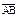 , если С(–2; 4; 1), В(– 4; 2; 3), а точка А является серединой отрезка СВ. , если С(–2; 4; 1), В(– 4; 2; 3), а точка А является серединой отрезка СВ.
| 1)
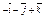
| 2)

| 3)
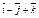
| 4)
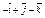
|
| 3.27 | Записать координаты вектора 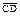 , если С(5; 1; 3), К(3; 1; 7), а точка К является серединой отрезка СD , если С(5; 1; 3), К(3; 1; 7), а точка К является серединой отрезка СD
| 1)
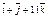
| 2)
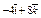
| 3)
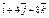
| 4)
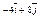
|
| 3.28 | Записать координаты вектора 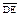 , если D(3; –1; 4), В(–3; –5; 6), а точка Е является серединой отрезка DВ , если D(3; –1; 4), В(–3; –5; 6), а точка Е является серединой отрезка DВ
| 1)
–3 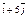
| 2)
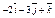
| 3)
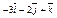
| 4)
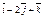
|
| 3.29 | Записать координаты вектора 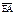 , если А(–3; 2; –5), В(–1; –4; 1), а точка Е является серединой отрезка АВ , если А(–3; 2; –5), В(–1; –4; 1), а точка Е является серединой отрезка АВ
| 1)
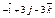
| 2)
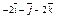
| 3)
3 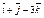
| 4)
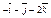
|
| 3.30 | Записать координаты вектора 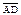 , если А(1; 1; 1); В(0; –1; 2), а точка B является серединой отрезка АD , если А(1; 1; 1); В(0; –1; 2), а точка B является серединой отрезка АD
| 1)
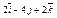
| 2) (–2; –4; 2) | 3)

| 4) (2; 4; 2) |
Задание 4.Ответить на вопрос задания, выбрав один из вариантов ответов.
Задание оценивается в 1 балл.
| Номер задания | Вопрос задания | Варианты ответов | |||
| 4.1 | Если два вектора 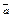 и и 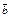 связаны соотношением связаны соотношением 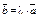 , где , где 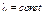 , то можно утверждать, что они… , то можно утверждать, что они…
| 1) коллинеарны | 2) ортого-нальны | 3) равны | 4) имеют одинаковое направление |
| 4.2 | Соответствующие координаты векторов 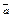 и и 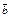 пропорциональны. Тогда можно утверждать, что эти векторы … пропорциональны. Тогда можно утверждать, что эти векторы …
| 1) равны | 2) ортого-нальны | 3) коллинеарны | 4) имеют одинаковую длину |
| 4.3 | Если у векторов 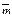 и и 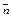 соответствующие координаты различны, то эти векторы … соответствующие координаты различны, то эти векторы …
| 1) равны по длине | 2) не равны | 3) неколлинеарны | 4) ортогональны |
| 4.4 | Если два вектора  и и 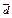 связаны соотношением связаны соотношением 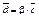 , где , где  , то можно утверждать, что эти векторы … , то можно утверждать, что эти векторы …
| 1) равны | 2) ортогональны | 3) неколлинеарны | 4) не равны |
| 4.5 | Если у векторов  и и 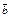 соответствующие координаты равны. Тогда можно утверждать, что эти векторы … соответствующие координаты равны. Тогда можно утверждать, что эти векторы …
| 1) равны | 2) ортогональны | 3) неколлинеарны | 4) не равны |
| 4.6 | Координаты векторов 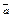 и и 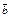 связаны соотношениями связаны соотношениями 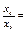 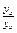 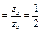 , тогда можно утверждать, что … , тогда можно утверждать, что …
| 1)
вектор 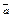 в 2 раза длиннее вектора
в 2 раза длиннее вектора 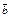
| 2) противоположны по направлению | 3)
вектор 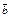 в 2 раза длиннее вектора в 2 раза длиннее вектора 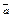
| 4) векторы равны |
| 4.7 | Координаты векторов 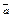 и и 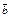 связаны соотношениями связаны соотношениями 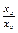 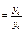 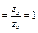 , тогда можно утверждать, что они … , тогда можно утверждать, что они …
| 1) равны | 2) не равны | 3) ортогональны | 4) противоположны по направлению |
| 4.8 | Координаты векторов 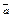 и и 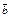 связаны соотношениями связаны соотношениями 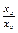 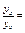 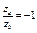 , тогда можно утверждать, что они … , тогда можно утверждать, что они …
| 1) противо- положны по направлению | 2) не равны | 3) ортогональны | 4) имеют одинаковое направление |
| 4.9 | Известно, что векторы  и и 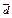 коллинеарны, имеют одинаковую длину, но противоположны по направлению, тогда коллинеарны, имеют одинаковую длину, но противоположны по направлению, тогда 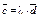 , где , где  равно… равно…
| 1) | 2) –1 | 3) | 4) |
П р о д о л ж е н и е
| 4.10 | Векторы  и и 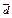 коллинеарны, имеют одно и то же направление, причем вектор коллинеарны, имеют одно и то же направление, причем вектор  в 2 раза короче вектора в 2 раза короче вектора 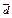 . Тогда . Тогда 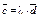 , где , где  равно… равно…
| 1)
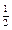
| 2) | 3) –2 | 4)
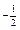
|
| 4.11 | Векторы  и и 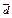 коллинеарны, имеют одно и то же направление, причем коллинеарны, имеют одно и то же направление, причем 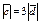 , тогда , тогда 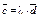 , где , где  равно… равно…
| 1) | 2)
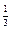
| 3) –3 | 4)
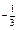
|
| 4.12 | Векторы  и и 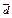 коллинеарны, имеют одно и то же направление и вектор коллинеарны, имеют одно и то же направление и вектор  в 2 раза длиннее вектора в 2 раза длиннее вектора 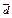 , тогда , тогда 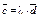 , где , где  равно… равно…
| 1) | 2) –2 | 3)
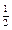
| 4)
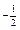
|
| 4.13 | Векторы  и и 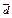 коллинеарны, имеют противоположные направления и вектор коллинеарны, имеют противоположные направления и вектор  в 2 раза длиннее вектора в 2 раза длиннее вектора 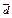 , тогда , тогда 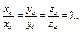 где где  равно … равно …
| 1) | 2) –2 | 3)
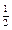
| 4)
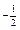
|
| 4.14 | Векторы  и и 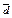 равны. Тогда равны. Тогда 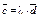 , где , где  равно… равно…
| 1) | 2) –1 | 3) | 4) |
| 4.15 | Векторы  и и 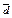 коллинеарны, имеют противоположные направления и вектор коллинеарны, имеют противоположные направления и вектор  в 2 раза короче вектора в 2 раза короче вектора 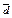 , тогда , тогда 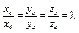 , где , где  равно… равно…
| 1)
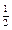
| 2) | 3) –2 | 4)
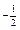
|
| 4.16 | Векторы  и и 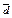 коллинеарны, имеют противоположные направления и вектор коллинеарны, имеют противоположные направления и вектор  в 4 раза длиннее вектора в 4 раза длиннее вектора 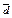 , тогда , тогда 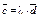 , где , где  равно… равно…
| 1) | 2)
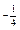
| 3) –4 | 4)
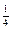
|
| 4.17 | Векторы  и и 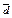 коллинеарны, имеют одно и то же направление, причем коллинеарны, имеют одно и то же направление, причем 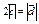 , тогда , тогда 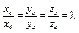 , где , где  равно… равно…
| 1) | 2) –2 | 3)
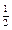
| 4)
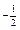
|
П р о д о л ж е н и е
| 4.18 | Векторы 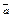 и и 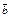 коллинеарны, имеют противоположные направления, причем вектор коллинеарны, имеют противоположные направления, причем вектор 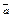 в 4 раза длиннее вектора в 4 раза длиннее вектора 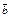 , тогда , тогда 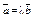 , где , где  равно… равно…
| 1) | 2) –4 | 3)
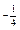
| 4)
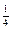
|
| 4.19 | Векторы 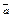 и и 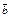 коллинеарны, имеют одно и то же направление, причем коллинеарны, имеют одно и то же направление, причем 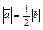 , тогда , тогда 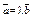 , где , где  равно… равно…
| 1) | 2) –2 | 3)
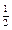
| 4)
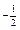
|
| 4.20 | Векторы  и и 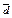 коллинеарны, имеют противоположные направления, причем коллинеарны, имеют противоположные направления, причем 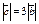 , тогда , тогда 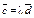 , где , где  равно… равно…
| 1) | 2) –3 | 3)
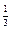
| 4)
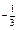
|
| 4.21 | Векторы  и и 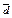 коллинеарны, имеют противоположные направления, причем вектор коллинеарны, имеют противоположные направления, причем вектор  в 5 раз длиннее вектора в 5 раз длиннее вектора 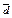 , тогда , тогда 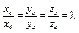 , где , где  равно… равно…
| 1) | 2) –5 | 3)

| 4)
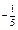
|
| 4.22 | Векторы 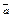 и и 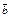 коллинеарны, имеют противоположные направления, причем коллинеарны, имеют противоположные направления, причем 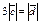 , , 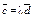 , где , где  равно… равно…
| 1)
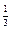
| 2)
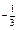
| 3) | 4) –3 |
| 4.23 | Векторы 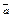 и и 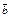 коллинеарны, имеют одно и то же направление, причем вектор коллинеарны, имеют одно и то же направление, причем вектор 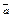 в 6 раз короче вектора в 6 раз короче вектора 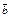 , тогда , тогда 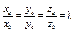 , где , где  равно… равно…
| 1)
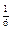
| 2)
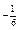
| 3) | 4) –6 |
| 4.24 | Векторы  и и 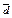 коллинеарны, имеют одно и то же направление, причем коллинеарны, имеют одно и то же направление, причем 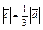 , тогда , тогда 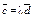 , где , где  равно… равно…
| 1)
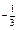
| 2) | 3) – 3 | 4)
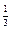
|
| 4.25 | Векторы  и и 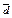 коллинеарны, имеют противоположные направления, причем коллинеарны, имеют противоположные направления, причем 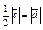 , тогда , тогда 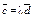 , где , где  равно… равно…
| 1)
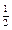
| 2)
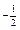
| 3) –2 | 4) |
О к о н ч а н и е
| 4.26 | Векторы  и и 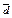 коллинеарны, имеют одно и то же направление, причем вектор коллинеарны, имеют одно и то же направление, причем вектор  длиннее длиннее 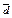 в 4 раза, тогда в 4 раза, тогда 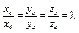 , где , где  равно… равно…
| 1) | 2) –4 | 3)
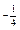
| 4)
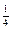
|
| 4.27 | Векторы 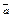 и и 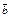 коллинеарны, имеют противоположные направления, длина вектора коллинеарны, имеют противоположные направления, длина вектора 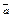 в 6 раз меньше длины вектора в 6 раз меньше длины вектора 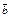 , , 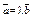 , тогда , тогда  равно… равно…
| 1) | 2) –6 | 3)
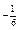
| 4)
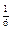
|
| 4.28 | Векторы 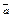 и и 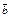 коллинеарны, имеют одно и то же направление и коллинеарны, имеют одно и то же направление и 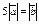 , тогда , тогда 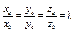 , где , где  равно… равно…
| 1) | 2) –5 | 3)
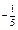
| 4)

|
| 4.29 | Векторы 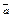 и и 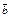 коллинеарны, имеют противоположные направления, причем коллинеарны, имеют противоположные направления, причем 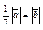 , тогда , тогда 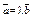 , где , где  равно… равно…
| 1) | 2)
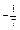
| 3)
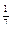
| 4) –7 |
| 4.30 | Векторы  и и 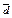 коллинеарны, имеют противоположные направления, причем коллинеарны, имеют противоположные направления, причем 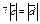 , тогда , тогда 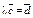 , где , где  равно … равно …
| 1)
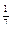
| 2)
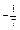
| 3) | 4) –7 |
Дата добавления: 2015-12-11; просмотров: 741;
