Прохождение волн через тонкий слой на границе двух сред
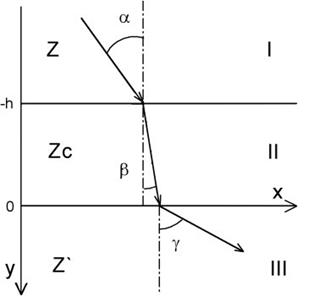
Рассмотрим общий случай наклонного падения продольной волны, считая для простоты все среды жидкими, так как в них не происходит трансформация типов волн (рис. 3.14).
|
| Рис. 3.14. Прохождение продольных волн через границу двух жидких сред, разделенных тонким слоем |
Для определения коэффициентов отражения 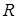 и прохождения
и прохождения 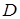 воспользуемся граничными условиями: давление и нормальные составляющие колебательных скоростей не меняются при переходе через границы слоя (здесь и далее слоем будем называть среду
воспользуемся граничными условиями: давление и нормальные составляющие колебательных скоростей не меняются при переходе через границы слоя (здесь и далее слоем будем называть среду 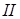 ).
).
Выражения для давления 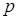 и нормальной составляющей колебательной скорости
и нормальной составляющей колебательной скорости 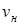 имеют вид:
имеют вид:
 , (3.45)
, (3.45)
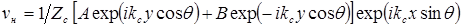 , (3.46)
, (3.46)
где 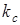 – волновое число в тонком слое;
– волновое число в тонком слое;
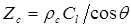 – нормальный импеданс тонкого слоя.
– нормальный импеданс тонкого слоя.
Зададим граничные условия.
1. На границе 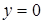 :
:
 , (3.47)
, (3.47)
где 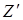 – входной нормальный импеданс для нижней границы.
– входной нормальный импеданс для нижней границы.
В данном случае 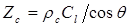 .
.
2. На границе 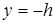 воспользуемся условием равенства суммарных импедансов сверху и снизу от границы:
воспользуемся условием равенства суммарных импедансов сверху и снизу от границы:
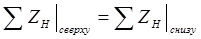 . (3.48)
. (3.48)
Используя это условие, найдем значение входного импеданса для верхней границы:
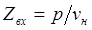 . (3.49)
. (3.49)
Тогда с учетом (3.45) и (3.46)
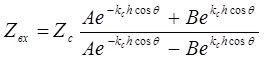 . (3.50)
. (3.50)
С учетом (3.47) получим
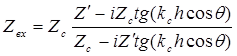 , (3.51)
, (3.51)
где 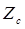 – нормальный импеданс слоя;
– нормальный импеданс слоя;
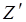 – нормальный импеданс нижней среды.
– нормальный импеданс нижней среды.
Таким образом, входной импеданс первой границы зависит от нормальных импедансов 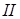 и
и 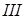 сред. Наличие мнимой части у
сред. Наличие мнимой части у 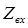 означает, что
означает, что 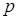 и
и 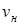 не совпадают по фазе. Из (3.51) нетрудно получить частный случай нормального падения волны. Тогда все соответствующие углы равны нулю, а их косинусы – единице. Нормальный же импеданс можно заменить характеристическим, поскольку они равны между собой. Как известно, коэффициент отражения волны от границы двух сред определяется по формуле
не совпадают по фазе. Из (3.51) нетрудно получить частный случай нормального падения волны. Тогда все соответствующие углы равны нулю, а их косинусы – единице. Нормальный же импеданс можно заменить характеристическим, поскольку они равны между собой. Как известно, коэффициент отражения волны от границы двух сред определяется по формуле
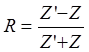 , (3.52)
, (3.52)
где 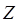 ,
, 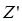 – нормальные импедансы сред.
– нормальные импедансы сред.
По аналогии можем записать коэффициент отражения от верхней границы для сред, разделенных тонким слоем, заменив 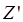 на
на 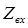 :
:
 , (3.53)
, (3.53)
где 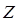 – нормальный импеданс среды (в случае нормального падения равен характеристическому).
– нормальный импеданс среды (в случае нормального падения равен характеристическому).
Формулу (3.51) можно вывести прямым решением уравнений из условий на границе, не используя понятие входного импеданса, как это было сделано выше. Ценность рассмотренного подхода в том, что можно распространить полученный результат на произвольное число слоев. В этом случае в уравнение (3.51) вместо 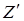 необходимо подставить входной импеданс для нижней границы слоя. Это применимо для всех последующих слоев. Если имеется два слоя, то
необходимо подставить входной импеданс для нижней границы слоя. Это применимо для всех последующих слоев. Если имеется два слоя, то 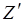 определяется по той же формуле, что и
определяется по той же формуле, что и 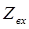 .
.
На практике возможным является использование слоев различной толщины. Проанализируем наиболее значимые с точки зрения эффективности АК соотношения.
1. Толщина слоя 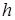 равна целому числу длин полуволн:
равна целому числу длин полуволн:
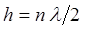 или
или 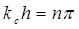 . (3.54)
. (3.54)
Тогда справедливо
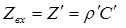 . (3.55)
. (3.55)
При этом коэффициент отражения определяется как
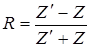 . (3.56)
. (3.56)
Последнее равенство означает, что при нормальном падении волны слой толщиной, равной или кратной половине волны, не влияет на отражение и прохождение, и коэффициенты отражения и прохождения зависят только от импедансов верхней и нижней сред.
В случае наклонного падения должно выполняться условие 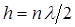 , при этом реализуется соотношение
, при этом реализуется соотношение 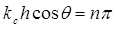 , что совпадает с условием возникновения нормальных волн Лэмба.
, что совпадает с условием возникновения нормальных волн Лэмба.
2. Если толщина слоя равна нечетному числу четвертей длин волн, т. е. 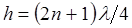 или
или 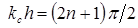 , то выражения для
, то выражения для 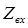 и
и 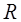 имеют вид
имеют вид
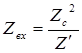 и
и 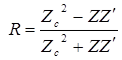 . (3.57)
. (3.57)
Таким образом, если толщина слоя кратна четверти длины волны, то слой влияет на отражение и прохождение волн через границу. В этом случае даже малое изменение толщины тонкого слоя может привести к существенному изменению коэффициентов отражения и прохождения.
Дата добавления: 2015-12-10; просмотров: 1741;
