Влияние толщины слоя на прохождение акустических волн

Известно, что при разделении сред тонким слоем возможно получение неодинаковых по величине коэффициентов отражения в зависимости от соотношения значений импедансов трех сред. Рассмотрим два случая.

1. Симметричный случай ( 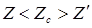или ).

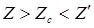Коэффициент отражения максимален 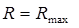при выполнении условия .

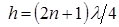Коэффициент отражения минимален 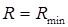при выполнении условия .

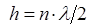2. Несимметричный случа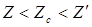й ( или ).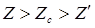

Коэффициент отражения максимален ( 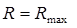) при выполнении условия 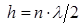. Коэффициент отражения минимален ( 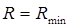) при выполнении условия .

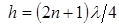Из приведенных соотношений видно, что четвертьволновый слой улучшает условия прохождения акустических волн через границу в несимметричном случае, а полуволновый – в симметричном. Таким образом, путем подбора материалов контактирующих промежуточных сред можно добиться эффекта просветления границ раздела, то есть добиться выполнения услови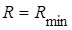й и 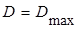. Особенно важно обеспечить реализацию этого эффекта при подборе материала и расчете толщины конструктивных элементов преобразователя.

Физической причиной осцилляции коэффициентов 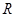и 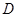при изменении толщины промежуточного слоя служит интерференция волн в тонком слое. Для иллюстрации рассмотрим преобразователь как комбинацию слоев (рис. 3.15).

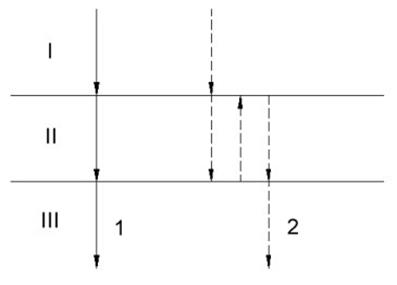
Рис. 3.15. Схема, поясняющая изменение фазы для сквозной волны (1) и волны (2), испытавшей двукратное отражение. I, II, III – среды с различными акустическими свойствами

На рис. 3.15. среда 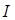– пьезопластина (импеданс 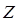), среда 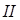– протектор (импеданс 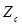), среда 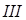– контактная жидкость (импеданс 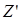). Для данной схемы реализуется несимметричный случай, т. е. .

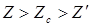Пусть толщина протектора равна четверти длины волны 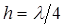. Изменение фазы для прошедшей волны с учетом толщины слоя протектора:

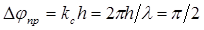. (3.58)

Изменение фазы однократно отраженной волны:

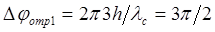. (3.59)

При отражении от нижней границы вследствие существенного различия импедансов сред произойдет изменение фазы на величину 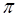. При отражении от верхней границы фаза останется прежней. При прохождении волны в среду III произойдет изменение фазы на 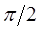. Общее изменение фазы для двукратно отраженной волны составляет:

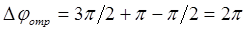. (3.60)

Таким образом, на нижней границе фазы прошедшей волны и волны, испытавшей двукратное отражение, совпадают. Вследствие этого происходит увеличение суммарной амплитуды волн, а значение коэффициента прозрачности для границы сред, разделенных тонким слоем, становится максимальным. В случае полуволнового слоя имеет место обратная ситуация: суммарная амплитуда на нижней границе уменьшается, а коэффициент прозрачности принимает минимальное значение.

Для случая очень тонкого слоя ( 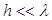) в симметричном случае ( 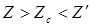) справедливо соотношение 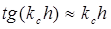. Тогда коэффициент отражения по интенсивности может быть определен по формуле:

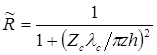. (3.61)

Эту модель можно использовать для описания эффектов отражения от различных дефектов типа трещин. Рассмотрим некоторые из них:

- малая трещина, заполненная воздухом ( 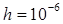мм), тогда для частоты 2,5МГц 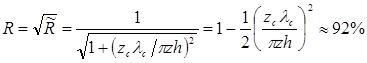и ;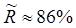

- трещина толщиной - ;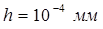

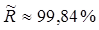- граница сталь – воздух (модель бесконечно широкой трещины), , .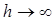

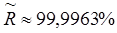Таким образом, видно, что коэффициент отражения будет близок к единице, если в зазоре между преобразователем и поверхностью объекта контроля отсутствует контактная жидкость. Если же этот зазор заполнен жидкостью, то в этом случае коэффициент отражения существенно уменьшается. Аналогичная ситуация имеет место также для заполненных дефектов и дефектов типа трещин с малым раскрытием, выявляемость которых гораздо ниже в сравнении с полыми дефектами того же размера.

Контрольные вопросы

1. Дайте определение коэффициентов прохождения и отражения по амплитуде и интенсивности. Как они зависят от значений акустических импедансов контактирующих сред?