Оценка воздействия взрыва на промышленные объекты
1.1 Основные параметры и свойства ударных волн при внешних взрывах
Ударные волны представляют большой интерес при изучении механического действия взрыва [1]. При распространении взрывных волн в воздухе или при взаимодействии их с каким–либо препятствием происходят быстрые изменения давления, плотности, температуры и массовой скорости.
По данным многочисленных исследований сформулированы основы элементарной теории ударных волн.
Фронт ударной волны можно рассматривать как поверхность, на которой претерпевают разрыв непрерывности параметры, характеризующие состояние и движение среды (рисунок 1), при этом на поверхности выполняются основные законы сохранения массы (1), количества движения (2) и энергии (3).
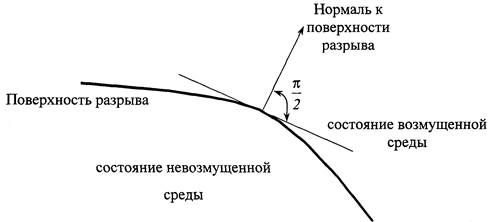
Рисунок 1 – Схематическое изображение фронта ударной волны
Состояние среды до и после разрыва характеризуется следующими параметрами: скоростью ударной волны, плотностью среды, скоростью потока среды.
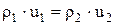 , ,
| (1) | |
 , ,
| (2) | |
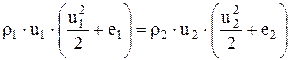 , ,
| (3) |
где ρ1, ρ2 – плотность среды соответственно до и после разрыва;
u1, u2 – скорость потока среды соответственно до и после разрыва;
р1, р2 – давление соответственно до и после разрыва;
е1, е2 – энтальпия, соответственно до и после разрыва.
В тех случаях, когда поток среды через поверхность разрыва существует, а тангенциальные компоненты скорости непрерывны на поверхности разрыва и равны нулю, поток среды движется по нормали к поверхности разрыва, то ударная волна прямая. Если же тангенциальные компоненты скорости не равны между собой по обеим сторонам разрыва и не равны нулю, то ударная волна – пространственная косая. В случае, если один из тангенциальных компонентов скорости равен нулю, такая волна будет плоской и называться просто косой ударной волной.
Далее будем рассматривать именно плоскую прямую ударную волну, так как она является наиболее приемлемой моделью, хотя и упрощенной.
Наиболее изученными являются невозмущенные каким–либо препятствием взрывные волны в воздухе. Такие волны принято называть падающими или проходящими. Структура подобных волн представлена на рисунке 2.
Взрывная волна ослабляется по мере ее распространения. По характеру воздействия она подразделяется на три зоны:
– ближайшая к источнику взрыва зона – характеризуется огромными давлениями и температурами;
– промежуточная зона, в которой избыточное давление достаточно велико для тяжелых разрушений;
– зона слабого взрыва, в которой возможно установление зависимости изменения избыточного давления во времени на больших расстояниях.
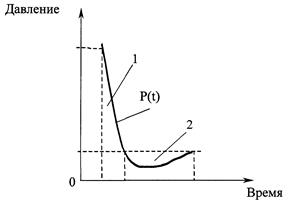
1 – положительная фаза; 2 – отрицательная фаза (волна разрежения)
Рисунок 2 – Структура идеальной взрывной волны
На основании исследований, можно отметить следующие основные свойства ударных волн, которые необходимо учитывать при определении нагрузок, действующих на конструкцию при прохождении воздушной ударной волны:
– скорость распространения ударных волн всегда больше скорости звука в невозмущенной среде;
– на фронте ударной волны параметры состояния и движения среды изменяются скачком;
– ударные волны сопровождаются перемещением среды в направлении распространения фронта возмущения;
– скорость ударной волны зависит от ее интенсивности;
– ударная волна не имеет периодического характера, а распространяется в виде одиночного скачка уплотнения;
– при встрече проходящей волны с объектом ограниченных размеров происходит отражение и дифракция ударных волн;
– при прохождении воздушной взрывной волны в грунте образуются ударные волны, которые взаимодействуют с объектом.
При решении конкретных прикладных задач к основным параметрам, характеризующим разрушающую способность взрывной волны, относят избыточное давление (Δр), которое представляет собой разность между максимальным давлением взрыва и начальным давлением среды и удельный импульс взрыва (i). Законы изменения нагрузок во времени, при решении прикладных задач, заменяют упрощенными – расчетными.
Известно, что давление в волне – есть функция скорости выделения энергии при сгорании объема газовой смеси, а импульс волны – слабая функция скорости тепловыделения.
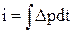 . .
| (4) |
Для удобства исследований, основные параметры ударной волны принято выражать как функции скорости звука в невозмущенной среде.
Для определения зависимостей по расчету параметров ударных волн следует использовать поля параметров, установленные для наиболее опасного режима – детонации.
Конкретный вид зависимости находят, как правило, в опытах с зарядами взрывчатых веществ. В связи с наличием в литературе большого количества информации о разрушительном действии взрывов конденсированных взрывчатых веществ, действие других источников ударных волн для практических приложений принято выражать тротиловым эквивалентом.
Соответствующая зависимость для избыточного давления на фронте ударной волны может быть описана общеизвестным уравнением
 , ,
| (5) |
где r – расстояние от центра облака до точки измерения, м;
W – масса тротила, энергия которого равна энергии взрывающейся газовой смеси, кг.
К сожалению, данных по измерению импульса на фазе сжатия известно значительно меньше, чем по измерениям избыточного давления, а также более низка их точность. Характер изменения импульса ударной волны аналогичен изменению избыточного давления. На основе имеющихся данных численное значение импульса можно определить по зависимости
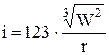 . .
| (6) |
Однако давление в падающей волне не представляет истинную нагрузку, действующую на объект после взрыва. Поэтому для того, чтобы оценить верхний предел таких нагрузок или дать приближенное значение ударных нагрузок, используют дополнительные параметры взрывной волны: динамическое давление или скоростной напор ударной волны (Q), которое в значительной мере определяет лобовую нагрузку и возможное повреждение объекта, а также скорость ударной волны (D).
Динамический (скоростной) напор ударной волны определяется согласно
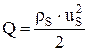 , ,
| (7) |
где  – плотность течения на фронте взрывной волны, кг/м3;
– плотность течения на фронте взрывной волны, кг/м3;
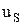 – скорость течения на фронте взрывной волны, м/с.
– скорость течения на фронте взрывной волны, м/с.
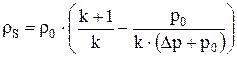 , ,
| (8) |
где 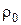 – начальная плотность газа, кг/м3, для воздушных взрывов
– начальная плотность газа, кг/м3, для воздушных взрывов 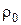 = 1,293 кг/м3;
= 1,293 кг/м3;
k – показатель адиабаты, значение k обычно находится в диапазоне от 1,2 до 1,4, причем для газовых смесей  ;
;
р0 – начальное давление (р0 =100 кПа).
 , ,
| (9) |
где D – скорость движения фронта ударной волны, м/с;
с – скорость звука в невозмущенном газе, м/с; для воздушных взрывов с = 333 м/с.
 , ,
| (10) |
где Δр – избыточное давление на фронте ударной волны, Па.
Процесс воздействия взрывной волны на реальные промышленные объекты усложняется из–за явления дифракции взрывных волн на конструкциях конечного размера. Вместе с отражением части волны от фронтальной поверхности объекта одновременно происходит дифракция волны вокруг самого объекта, при этом фронт волны вновь смыкается за телом. При встрече взрывной волны с препятствием давление, действующее на объект, скачкообразно возрастает, а затем, при обтекании, уменьшается.
При протекании взрывного процесса в атмосфере, кроме вышеописанных явлений, возникают еще ударные волны в грунте, независимо от положения источника взрыва относительно земли. Параметры ударных волн в грунте зависят от расстояния от центра заряда, параметров порождающей воздушной ударной волны, характеристик грунта. Учет взаимодействия ударных волн в грунте с сооружениями особенно важен при подземных взрывах и при действии на заглубленные конструкции, колебания грунта при наземных и воздушных взрывах, а также создаваемые нагрузки могут повлиять на работоспособность объекта. В данной работе взаимодействие объектов с волнами в грунте рассматриваться не будет.
1.2 Методика определения ударной нагрузки, действующей на аппараты колонного типа при внешнем взрыве
Особый интерес представляет этап определения расчетных нагрузок, действующих при внешнем взрыве на аппараты колонного типа. В зависимости от степени устойчивости сооружения на действие взрыва и его удаления от источника они могут быть как аварийными, так и эксплуатационными. При эксплуатационных нагрузках в конструкциях не должны возникать деформации, приводящие к нарушению нормальной работы сооружения, тогда как при аварийных нагрузках могут возникать пластические деформации и разрушения. В большинстве случаев нагрузки, вызванные действием взрывных волн, являются для конструкций аварийными, и они значительно превосходят эксплуатационные нагрузки.
Стандартные методы расчета на прочность и определение расчетных усилий, возникающих в элементах аппаратов колонного типа постоянного и переменного по высоте сечений от ветровых нагрузок и сейсмических воздействий, проводятся в соответствии с требованиями. Методы расчета заключаются в следующем:
– устанавливаются опасные сечения, для которых и будет проводиться расчет;
– определяются расчетные нагрузки (от давления, температуры, от действия эксцентричных весовых сил, ветровых нагрузок и сейсмических воздействий) в опасных сечениях;
– определяются нагрузки для трех различных условий работы (эксплуатации, испытаний, монтажа);
– проводят стандартную проверку выполнения условий прочности и устойчивости стенки колонного аппарата;
– проводят стандартный расчет на прочность и устойчивость опорной обечайки, в результате которого проверяют прочность сварного шва, соединяющего корпус аппарата с опорной обечайкой, и устойчивость самой обечайки;
– проводят стандартный расчет нижнего опорного узла, в результате которого определяют размеры опорного узла, удовлетворяющие условиям прочности и устойчивости;
– проводят расчет анкерных болтов, который заключается в выборе количества болтов и расчете внутреннего диаметра их резьбы, а затем, проверяют выполнение условия прочности.
Взрывные волны действуют на конструкции и сооружения как кратковременные динамические нагрузки, которые значительно превосходят эксплуатационные и являются аварийными. Расчет напряжений, прогибов и деформаций в элементах конструкций при воздействии взрыва необходим для выяснения уровня повреждения объекта. Как правило, требуется информация о максимальных напряжениях и деформациях при изгибе и сдвиге, а не о динамике деформируемого состояния, поэтому целесообразно использовать упрощенные аналитические методы оценок, позволяющие представить результаты расчетов графически. Это дает возможность установить влияние изменения различных параметров нагрузок на деформации в конструкции.
В расчетах аппараты колонного типа обычно принимают как вертикальный консольный стержень постоянного или переменного сечения, упруго защемленный у основания.
Целесообразно рассматривать колонный аппарат как упругую систему (по аналогии на действие ветровой и сейсмической нагрузки). В приведенной ниже методике определения ударных нагрузок на аппараты колонного типа используются упрощенные аналитические методы, и нагрузка принимается равномерно распределенной по высоте конструкции (рисунок 3).
В качестве модели взрыва рассматриваем случайный наземный взрыв неограниченного парогазового облака в воздушной среде (атмосфере) при нормальных условиях с плоским прямым фронтом ударной волны.
Взрывная волна может оказать разрушающее действие только на отдельные элементы конструкции (локальное действие) или на всю конструкцию (общее действие). В зависимости от эксплуатационных требований допускаются:
– только упругие деформации;
– пластические деформации;
– выход из строя отдельных элементов конструкции без разрушения всего сооружения.
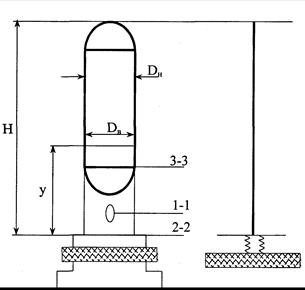
Рисунок 3 – Расчетная схема колонного аппарата
Нагрузку, создаваемую ударной волной на колонный аппарат в целом или на участок высотой ((Н – у), м) при внешнем взрыве, можно представить как
 , ,
| (11) |
где 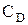 – коэффициент сопротивления тела стационарному обтекающему потоку воздуха, или аэродинамический коэффициент; для колонного оборудования, ось симметрии которого перпендикулярна направлению потока;
– коэффициент сопротивления тела стационарному обтекающему потоку воздуха, или аэродинамический коэффициент; для колонного оборудования, ось симметрии которого перпендикулярна направлению потока;
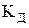 – коэффициент динамического усиления;
– коэффициент динамического усиления;
q – нагрузка, действующая на аппарат при обтекании его ударной волной, распределенная по высоте аппарата, Н/м;
Н – высота колонны, м;
у – ордината произвольного расчетного сечения, м.
Лобовую нагрузку, действующую на объект при взрыве, определяет динамическое давление, поэтому распределенную нагрузку, действующую на аппарат колонного типа при обтекании его взрывной волной, можно представить как
 , ,
| (12) |
где Q – динамический (скоростной) напор ударной волны, Па, рассчитываемый по формуле (7);
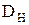 – наружный диаметр колонны, м.
– наружный диаметр колонны, м.
При решении динамических задач существует подход, по которому динамические величины можно определить путем умножения статических величин на динамический коэффициент. В данной задаче коэффициент динамического усиления
 , ,
| (13) |
где  – характеризует долю усиления динамической составляющей взрывной нагрузки;
– характеризует долю усиления динамической составляющей взрывной нагрузки;
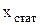 – статический прогиб от действия ударной волны, м.
– статический прогиб от действия ударной волны, м.
Поскольку объекты цилиндрической формы хорошо обтекаемы, величину статического прогиба при дифракции взрывной волной характеризует давление, действующее на сооружение в момент установления режима обтекания
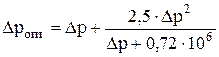 , ,
| (14) |
где  – давление обтекания, Па;
– давление обтекания, Па;
 – избыточное давление на фронте ударной волны, Па.
– избыточное давление на фронте ударной волны, Па.
Максимальный статический прогиб от действия взрывной волны
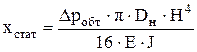 . .
| (15) |
Для расчета максимального прогиба в режиме импульсного приложения нагрузки используется известный закон сохранения энергии, то есть равенства кинетической энергии ударной волны (К, Дж) и потенциальной энергии деформации, (U, Дж)
| K=U | (16). |
Полная кинетическая энергия ударной волны в режиме импульсного приложения определяется
 , ,
| (17) |
где I – полный импульс ударной волны, Н·с;
m – общая масса аппарата при рабочих условиях, кг.
Максимальная потенциальная энергия деформации, накопленная системой, определяется следующим образом
 , ,
| (18) |
где М – изгибающий момент, Н*м.
Потенциальная энергия деформации, накопленная упругой системой, при условии малой деформации (упругий изгиб Бернулли) определяется из выражения
 , ,
| (19) |
где 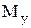 – изгибающий момент, возникающий в упругой системе, Н·м;
– изгибающий момент, возникающий в упругой системе, Н·м;
Е – модуль упругости материала аппарата, Па;
J – момент инерции аппарата относительно центральной оси, м4.
Одним из основных моментов в решаемой задаче является выбор подходящей формы колебаний х=f(у), форма колебаний существенно не влияет на энергетические оценки при расчете деформаций, поэтому в пределах допускаемой погрешности получается достоверное приближенное решение независимо от формы колебаний, удовлетворяющей соответствующим граничным условиям.
Для рассматриваемой системы форма деформируемой оси должна удовлетворять следующим условиям:
– нулевой прогиб и угол поворота в заделке ( 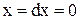 и
и 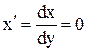 );
);
– максимальный прогиб на свободном конце;
– отсутствие момента сил на свободном конце (нулевая вторая производная,  ).
).
Известно, что этим условиям отвечает колебание, соответствующее линии статического прогиба (рисунок 4).
Для того, чтобы получить уравнение кривой статического прогиба по высоте, запишем прогиб в произвольном сечении, определенный по методу начальных параметров для единичной распределенной нагрузки (q* = 1 Н/м) и при единичных характеристиках колонного аппарата (Е = 1 Па, J = 1 м4).
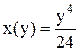 . .
| (20) |
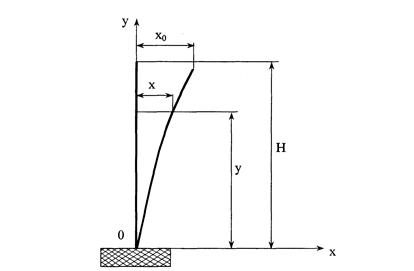
Рисунок 4 – Схема изгиба аппарата колонного типа
под действием ударной нагрузки
Дважды продифференцировав выражение (20) и поделив правую часть выражений на максимальные соответствующие величины, запишем уравнения прогиба, угла поворота и упругой линии балки относительно максимальных:
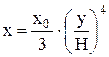 , ,
| (21) | |
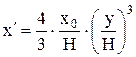 , ,
| (22) | |
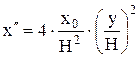 , ,
| (23) |
где  – максимальный прогиб, м.
– максимальный прогиб, м.
Подставив в (19) выражение для  , запишем выражение полной потенциальной энергии для рассматриваемой упругой системы:
, запишем выражение полной потенциальной энергии для рассматриваемой упругой системы:
 , ,
| (24) | |
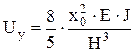 . .
| (25) |
Максимальный прогиб  в режиме импульсного приложения нагрузки определяем из равенства потенциальной энергии деформации и кинетической энергии (16).
в режиме импульсного приложения нагрузки определяем из равенства потенциальной энергии деформации и кинетической энергии (16).
 . .
| (26) |
Отсюда
 . .
| (27) |
Тогда, подставив (27) в (13), получаем коэффициент динамического усиления упругой системы
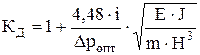 . .
| (28) |
Подставляя выражение (28) в (11), получаем формулу для определения нагрузки, создаваемой ударной волной, на колонный аппарат в целом при внешнем взрыве
 . .
| (29) |
Таким образом, получена зависимость нагрузки, действующей на колонное оборудование при действии взрывной волны. Далее по известной формуле рассчитывается изгибающий момент от действия ударной волны в опасных сечениях
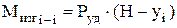 . .
| (30) |
Затем проводят проверку аппарата на прочность и устойчивость.
Результатом этих расчетов является оценка живучести колонных аппаратов, которая заключается в проверке прочности и устойчивости формы конструкций при различных уровнях воздействия взрывной волны.
2 Оценка прочности колонных аппаратов под действием внешнего взрыва с учетом наличия трещин
При оценке прочности колонных аппаратов необходимо учесть имеющиеся в конструкции дефекты и оценить их влияние на прочность.
Любой материал, какой бы предварительной технологической обработке он ни подвергался, всегда обладает какими–либо несовершенствами. Он содержит дефекты, присущие как самому материалу, так и те, которые возникают в процессе изготовления изделия.
Колонные аппараты изготавливаются сопряжением различных оболочек термической сваркой. При этом анализ работы аппаратов позволяет выявить преимущественные места возникновения дефектов. Эти очаги можно разделить на три основные группы:
– сварные швы или участки, прилегающие к местам сварки;
– места концентрации напряжений, обусловленные формой элемента;
– местные повреждения (трещины, царапины, вмятины, подрезы и т.п.), появившиеся при изготовлении отдельных элементов или при некачественной обработке.
Наиболее часто имеют место трещины в зоне сварных швов. В самих сварных швах возникает сетка мелких трещин, а в околошовной зоне трещины достигают глубины 20 мм (при толщине стенки аппарата 30 мм), а в длину вырастают до 1,5 м и более. Эти дефекты являются очагами, вблизи которых начинаются разрушения.
Разрушения возникают в связи с тем, что в процессе эксплуатации первоначально безопасные трещины могут начать расти и достичь критических размеров; при этом коэффициент интенсивности напряжений (даже не превышающих допускаемые напряжения) будет возрастать до опасной величины.
Рассмотрим так называемую идеализированную модель хрупкого разрушения, основанную на концепциях Гриффитса, Ирвина, поскольку в условиях динамических взрывных нагрузок эта модель является наиболее подходящей. Рост прямолинейной трещины рассматривается в упругой плоскости. При этом в вершине возникают неограниченные по величине напряжения, и процесс разрушения предполагается происходящим собственно в самой вершине трещины. Кроме того, предполагается, что расход энергии на образование единицы новой поверхности является константой для данного материала.
Рассмотрим процесс развития трещин в конструкциях, приводящий к авариям вследствие быстрого разрушения. Николс этот процесс делит на три стадии:
1 трещина медленно растет, начиная от концентратора или дефекта, под влиянием приложенных однократных или переменных напряжений. Известно, что этот процесс ускоряется под воздействием окружающей химической среды;
2 трещина, достигнув критического размера, становится нестабильной, т.е. может распространяться без дальнейшего увеличения приложенных напряжений. Это состояние зависит от локальных свойств материала, местной величины напряжений и окружающей среды;
3 нестабильная трещина, начинающаяся в месте, где наблюдается наиболее жесткое сочетание условий по напряжениям, свойствам материала и среды по сравнению с условиями для всей конструкции, может либо пройти через все тело конструкции, либо остановиться на каком–то расстоянии от места зарождения.
Хрупкое разрушение может начинаться в изолированных областях локального охрупчивания – твердых включениях, прожогах, хрупких сварных швах и т.д., трещиностойкость которых ниже, чем у основного материала.
Рассмотрим аппарат колонного типа с трещиной (рисунок 5) под действием ударной нагрузки и выделим элемент с трещиной.

Рисунок 5 – Расчетная схема аппарата с трещиной
Критические размеры трещины определяет критерий хрупкого разрушения КIс: критическая длина трещины
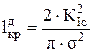 ; ;
| (31) |
критическая глубина
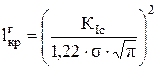 ; ;
| (32) |
где КIс – критический коэффициент интенсивности напряжений, МПа · м1/2;
σ – напряжения от максимальной нагрузки на аппарат от действия внешнего взрыва, МПа.
Предлагается следующий порядок расчета напряжений от максимальной нагрузки на аппарат (σ, Па):
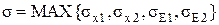 ; ;
| (33) |
где σх1 – меридиональные напряжения со стороны взрыва (по аналогии с ветровой нагрузкой), Па;
σх2 – меридиональные напряжения с противоположной от взрыва стороны колонны, Па;
σЕ1 – эквивалентные напряжения со стороны взрыва, Па;
σЕ2 – эквивалентные напряжения с противоположной от взрыва стороны, Па.
Меридиональные напряжения определяются по формулам:
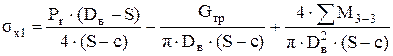 , ,
| (34) | |
 , ,
| (35) |
где Рr – расчетное давление в аппарате, Па;
Dв – внутренний диаметр аппарата, м;
S – толщина стенки аппарата, м;
с – прибавка к толщине стенки, м,
Gтр – вес участков колонны, расположенных выше трещины при рабочих условиях, Н;
ΣМ3-3 – изгибающий момент от совместного действия ветровой и ударной нагрузки в расчетном сечении 3–3 (место приварки корпуса аппарата к опоре), Н·м.
Эквивалентные напряжения рассчитываются по формулам:
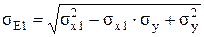 , ,
| (36) | |
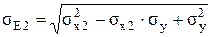 , ,
| (37) |
где σу – окружные напряжения (только от внутреннего давления в аппарате), Па:
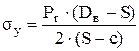 . .
| (38) |
Далее подставляя в формулы (31) и (32) найденные значения максимальных напряжений по (33) от действия взрывной нагрузки, определяем критические параметры трещины: ширину и глубину.
Цель расчета: оценка прочности колонного аппарата под действием внешнего взрыва с учетом наличия трещины.
3 Пример решения
Задача
На расстоянии r=200 м от дебутанизатора происходит надземный взрыв. Тротиловый эквивалент взрыва (W) - 2000 кг. В сварном шве основания колонны обнаружена трещина размером L=15 мм. Необходимо определить, является ли такая трещина критической с точки зрения безопасности дальнейшей эксплуатации.
Дебутанизатор изготовлен из стали марки 16ГС. Внутренний диаметр (Dв) 1600 мм; толщина стенки аппарата (S) - 8 мм; прибавка к толщине стенки с=2,5 мм; высота (Н) 26780 мм; масса колонны в рабочем состоянии (m) 15800 кг; момент инерции колонны J=0,013 м4. Расчетное давление в аппарате Р=600 кПа. Допускаемое значение напряжения при рабочей температуре 148 МПа; модуль продольной упругости Е=198,2 ГПа. За расчетное сечение принято сечение на высоте у3-3=2 м. Расчетная схема колонного аппарата приведена на рисунке 3. Изгибающий момент от ветровой нагрузки в расчетном сечении равен: 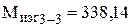 кН·м. Вес участков колонны, расположенных выше трещины,
кН·м. Вес участков колонны, расположенных выше трещины, 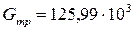 кг.
кг.
Показатель адиабаты принять равным k=1,3; критический коэффициент интенсивности напряжений КIс=13 МПа · м1/2.
Решение
Предполагаем, что трещина возникает в сварном шве приварки корпуса аппарата к опоре.
В расчете приняты следующие значения некоторых величин: начальное давление р0 =100 кПа; скорость звука для воздушных взрывов с = 333 м/с; для воздушных взрывов начальная плотность газа 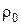 = 1,293 кг/м3; аэродинамический коэффициент
= 1,293 кг/м3; аэродинамический коэффициент 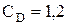 .
.
Расчет на прочность и устойчивость будем вести от совместного действия на аппарат ветровой и ударной нагрузок, которые принимаем равномерно распределенными по высоте колонны.
Рассчитаем параметры ударной волны (импульс и давление на фронте) по формулам (5) и (6):
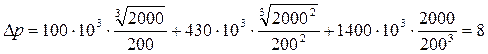 кПа, кПа,
| ||
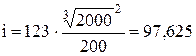 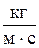 . .
|
Давление, действующее на сооружение в момент установления режима обтекания по формуле (14):
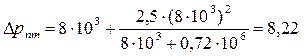 кПа. кПа.
|
Плотность течения на фронте ударной волны по формуле (8):
 кг/м3. кг/м3.
|
Скорость движения фронта ударной волны по формуле (10):
 м/с. м/с.
|
Скорость течения на фронте ударной волны по формуле (9):
 м/с. м/с.
|
Динамический напор ударной волны по формуле (7):
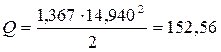 Па. Па.
|
Нагрузка, действующая на аппарат при обтекании его ударной волной по формуле (12):
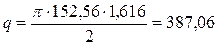 Н/м. Н/м.
|
Коэффициент динамического усиления по формуле (28):
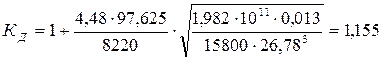 . .
|
Ударная нагрузка, рассчитанная по формуле (11) составит:
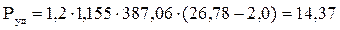 кН. кН.
|
Изгибающий момент от действия ударной нагрузки в расчетных сечениях соответственно по (30):
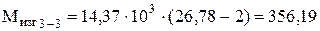 кН · м; кН · м;
|
Суммарный изгибающий момент от совместного действия ветровой и ударной нагрузки в расчетном сечении 3–3 соответственно:
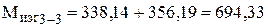 кН · м; кН · м;
|
Определим меридиональные напряжения по формулам (34) и (35), возникающие в колонном аппарате в месте обнаружения трещины со стороны взрыва ( 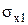 ) и со стороны противоположной взрыву (
) и со стороны противоположной взрыву (  ) соответственно:
) соответственно:
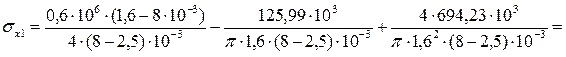 =107,37 МПа;
=107,37 МПа;
|
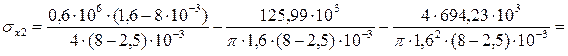 =/-20,53/ МПа.
=/-20,53/ МПа.
|
Окружные напряжения (только от внутреннего давления в аппарате) по формуле (38):
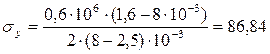 МПа. МПа.
|
Эквивалентные напряжения, возникающие в аппарате от совместного действия ветровой и ударной нагрузок, определяются по формулам (36) и (37):
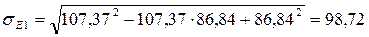 МПа; МПа;
| ||
 МПа. МПа.
|
Напряжения от максимальной нагрузки на аппарат от действия внешнего взрыва определяются по формуле (33):
 МПа; МПа;
|
Условие прочности и устойчивости корпуса аппарата выполняется, если максимальная нагрузка на аппарат не превышает допускаемых напряжений:
| 107,37 МПа < 148 МПа. |
Критические размеры трещины определяются по формулам (31) и (32).
Критическая длина трещины:
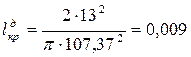 м; м;
|
критическая глубина:
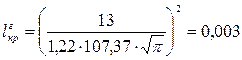 м. м.
|
Очевидно, что имеющаяся трещина (L = 15 мм) превышает по размерам критическую, следовательно, такая трещина небезопасна в случае внешнего взрыва.
Из проведенных расчетов видно, что наличие в конструкциях даже незначительных трещин, в случае воздействия на них взрывной нагрузки, способно привести к их росту, и в конечном итоге к потере прочности аппарата.
4 Перечень вариантов
Исходные данные для всех вариантов:
марка стали - 16ГС,
прибавка к толщине стенки - с=2,5 мм,
высота дебутанизатора - Н=26780 мм,
масса колонны - m=15800 кг,
момент инерции колонны - J=0,013 м4,
расчетное давление в аппарате - Ррасч=600 кПа,
допускаемые напряжения: [σ]200=148 МПа,
модуль упругости: Е=198,2 ГПа,
расчетное сечение - y3-3=2 м,
изгибающий момент от ветровой нагрузки - Мизг3-3=338,14 кН·м,
вес участков колонн расположенных выше трещины - Gтр=125,99·103 кг,
показатель адиабаты - K=1,3,
критический коэффициент интенсивности напряжений - K1c=13 МПа·м1/2
толщина стенки аппарата - S=8 мм.
В таблице 1 приведены дополнительные исходные данные для вариантов заданий.
Таблица 1 – Дополнительные исходные данные для вариантов заданий
| Номер варианта | W, кг | r, м | L, мм | Dвн, мм | |
| Продолжение таблицы 1 | |||||
| Продолжение таблицы 1 | |||||
| Продолжение таблицы 1 | |||||
5 Рекомендации по оформлению выводов по практической работе
Представить отчет по практической работе в рукописном или печатном виде, содержащий название практической работы, номер варианта, исходные данные, включая эскиз колонны, последовательность расчета, результаты расчета и выводы. Пример оформления титульного листа приведен в приложении А.
В выводах должна быть отражена оценка выполнения условия прочности и устойчивости корпуса колонного аппарата с учетом наличия трещины при воздействии ударной волны.
| <== предыдущая лекция | | | следующая лекция ==> |
| Календарь пчеловода | | | В опытах проводится точный количественный учет всех организмов последующих поколений, которые различаются по каждой паре изучаемых признаков. |
Дата добавления: 2015-12-08; просмотров: 3809;
