Лекция №7. Энергия ветра. Работа ветрового колеса крыльчатого ветродвигателя. Идеальный ветряк. Вертикально-осевая ветровая роторная турбина

Содержание лекции: энергия ветра, действие силы ветра на поверхность, работа ветрового колеса крыльчатого ветродвигателя, идеальный ветряк и его характеристики, мощность пропеллерного ветроколеса, конструкция и работа вертикально-осевой ветровой роторной турбины, автономная работа ВЭС и ее параллельная работа с энергосистемой.

Цель лекции:изучение основных положении теории ветроустановок,рассмотрение ветроэнергетических агрегатов различной конструкций и принципов их работы

Поток ветра с поперечным сечением F обладает кинетической энергией, определяемой выражением:

Масса воздуха, протекающая через поперечное сечение F со ско-ростью V, равна:

m = rFV. (2)

Тогда кинетическая энергия ветра:

Из (3) следует, что энергия ветра изменяется пропорционально кубу его скорости.

Посмотрим, сколько процентов энергии ветра может превратить в полезную работу поверхность, поставленная перпендикулярно к направлению ветра и перемещающаяся в этом же направлении, что имеет место, например, у ветродвигателей карусельного типа.

Мощность T определяется произведением силы P на скорость V:

T = PV. (4)

Допустим, мы имеем поверхность F, поставленную перпендику-лярно к направлению ветра (рисунок 1)

Рисунок. 1 -. Действие силы ветра на поверхность

Воздушный поток вследствие торможения его поверхностью получит подпор и будет обтекать её и производить давление силой Px. Вследствие действия этой силы поверхность будет перемещаться в направлении потока с некоторой скоростью U (рис. 7.10); работа Т при этом будет равна произведению силы на скорость U, с которой перемещается поверхность F, то есть:

где Px– сила сопротивления, которая равна:

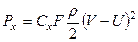
где Cx– аэродинамический коэффициент лобового сопротивления; F – поверхность миделевого сечения тела, т. е. проекции площади тела на плоскость, перпендикулярную направлению воздушного потока.

В этом случае ветер набегает на поверхность с относительной скоростью, равной:

W =V - U. (7)

Подставив значение Pxиз уравнения (7.3.6) в уравнение (7.3.5), получим:

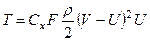(8)

Определим отношение работы, развиваемой движущейся поверхностью и выраженной уравнением (7.3.8), к энергии ветрового потока, имеющего поперечное сечение, равное этой поверхности, а именно:

(9)

Величину 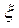называют коэффициентом использования энергии ветра, зависит от скорости перемещения поверхности в направлении ветра. При некотором значении скорости U коэффициент 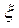получает максимальное значение. В самом деле, если скорость перемещения поверхности равна нулю U = 0, то работа ветра также равна нулю. Если U = V, т. е. поверхность перемещается со скоростью ветра, работа также будет равна нулю. Отсюда следует, что значение скорости U заключено в пределах между U = 0 и U = V. Установлено, чтобы получить максимальное 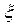поверхность должна перемещаться со скоростью:

U=V/3 (10)

Максимальный коэффициент использования энергии ветра при работе поверхности силой сопротивления не может быть больше 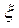= 0,192.