Дифракция электромагнитных волн

Все явления, связанные с особенностями распространения электромагнитной волны в неоднородной среде, которые невозможно описать в рамках геометрической оптики, относят к дифракции. Вначале под дифракцией понимали проникновение волны в область геометрической тени. Сейчас же круг дифракционных явлений настолько широк, что строгое определение дифракции вряд ли возможно. Даже то, что я сказал о геометрической оптике, может быть оспорено. Например, в последнее время физики интенсивно изучают среды с “отрицательным” показателем преломления (В.Г.Веселаго, 1968) в рамках формальной геометрической оптики. На рис.54.1 показано распространение электромагнитной волны, падающей на границу раздела двух сред с показателями преломления 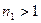и .

Рис.54.1

В этом случае преломленная волна идет в соответствии с законом Снеллиуса (52.2) не в том направлении, как обычно, а так, как показано на рисунке. Можно долго рассуждать о формализме описания сред, для которых показатель преломления отрицателен. Однако, можно не определять отрицательного показателя преломления, а решить эту задачу, как задачу дифракции волны на периодической структуре (она показана кружочками), поскольку только в таких средах наблюдается аномальный ход лучей.

Прежде чем перейдем к рассмотрению частных задач дифракции, отметим важнейшее условие. Если длина волны сравнима с характеристическим размером неоднородности среды, в которой она распространяется, то явления дифракции проявляются максимально. Если же она много меньше размера неоднородности, то описать распространение волны можно, используя законы отражения и преломления волн в рамках геометрической оптики. Если же длина волны много больше размера неоднородности, то принято говорить о ее рассеянии.

При решении задач дифракции мы пользуемся принципом суперпозиции полей, который в этом разделе физики называют принципом Гюйгенса-Френеля. Он заключается в том, что каждая точка волнового фронта (бесконечно малый элемент его поверхности) становится источником вторичных волн. Интенсивность излучения в произвольной точке наблюдения будет являться результатом интерференции множества этих вторичных волн. В вакууме, конечно, этот принцип не имеет никакого физического содержания, в среде же мы можем считать источниками этих вторичных волн заряды, колеблющиеся в поле падающей волны.

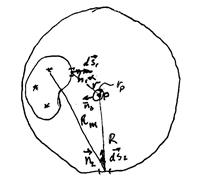
Обоснование принципа Гюйгенса-Френеля на основе решения волнового уравнения было сделано Кирхгофом (G.Kirchhoff, 1882). Пусть имеется источников света. Они расположены в объеме, ограниченном замкнутой поверхностью 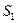, на которой будем считать, в соответствии с принципом Гюйгенса-Френеля, находятся источники вторичных волн. Один из них показан на рис.54.2 – излучающая площадка .

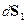Окружим точку наблюдения сферической поверхностью радиуса 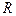и решим волновое уравнение в двусвязной области пространства между замкнутыми поверхностям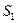и и 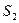. Односвязной называется область, в которой любая замкнутая поверхность может быть стянута в точку. Если бы замкнутой поверхности 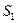не было, то объем, ограниченный замкнутой поверхностью 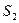, представлял собой односвязную область пространства.

Для монохроматичной волны переменные в уравнении (23.2) разделяются, и мы получаем уравнение для пространственного распределения

напряженности поля:

. (54.1)

Это уравнение будет одинаковым для любой проекции вектора

напряженности электрического поля.

Рис.54.2

Далее решаем задачу для какой-то одной линейно поляризованной волны. Введем вспомогательную функцию 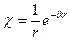. Подстановкой убедимся, что она также будет удовлетворять уравнению

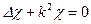. (54.2)

Функция 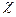- сферически симметричная функция, поэтому в операторе Лапласа будет только слагаемое, зависящее от 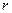так, что

.

Для исключения расходимости решения уравнения (54.1) в точке наблюдения Р (при 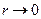, 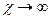) окружим ее сферической поверхностью малого радиуса 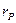. Для решения уравнения, теперь уже в трехсвязной области, воспользуемся формулой Грина (Т.Корн, Г.Корн. Справочник по математике, 1984, с.175). С выводом ее для двух непрерывных функций и 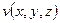с непрерывными производными можно познакомиться, например, в книге А.Н.Тихонова и А.А.Самарского (Уравнения математической физики, 1977, с.288-293). Итак, используя формулу Грина, можем записать:

.

Интеграл слева равен нулю, поскольку подынтегральное выражение можем получить, умножая (54.1) на 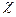, и вычитая результат умножения (54.2) на , оно оказывается равно нулю.

В интеграле справа производные берутся по направлениям единичных векторов для каждой поверхности, показанных на рис.54.2. Интеграл справа распадается на три интеграла:

.

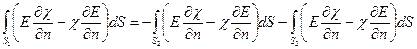Второй интеграл справа вычислим, устремляя к нулю:

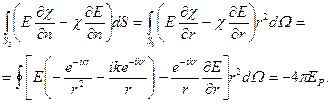
Интеграл по поверхност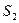и при 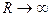будет стремиться к нулю.

Докажем это утверждение. Электрическое поле в волне убывает обратно пропорционально расстоянию до источника, тогда электрическое поле в произвольной точке на сферической поверхности радиуса 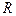будет равно:

.

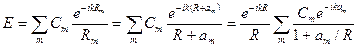Раскладывая функцию 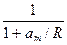в ряд по малому параметру 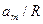, получим

,

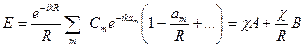где 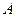и - постоянные не зависящие от 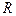. В разложении мы ограничились первыми двумя слагаемыми.

Вернемся теперь к интегралу по поверхност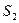и при :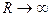

.

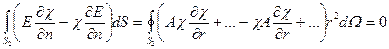Остальные слагаемые, которые убывают с ростом 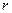быстрее чем 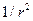, не приведены. Слагаемые, которые могли дать ненулевой вклад, одинаковы по величине и противоположны по знаку.

Окончательно получили следующий результат: электрическое поле в точке наблюдения 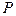получаем в результате сложения полей всех волн, излученных вторичными источниками на волновом фронте 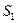. Сумму записываем в виде интеграла:

.

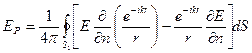При решении практических задач, вместо замкнутой поверхности берем поверхность открытого участка волнового фронта источника. Например, если имеется полость с источником внутри и открытым участком 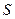, то напряженность поля в точке наблюдения, после вычисления производной в первом слагаемом, будет равна:

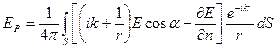. (54.3)

Для большинства задач по дифракции света в последнем уравнении делают еще одно упрощение: пренебрегают вторым слагаемым в круглых скобках, считая .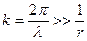

Рассмотрим простейшую задачу дифракции плоской волны на щели (рис.54.3а). Пусть ширина щели равна 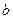, а длину ее считаем бесконечно большой. Тогда любая полоска шириной 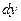будет излучать цилиндрическую волну. Никаких перераспределений интенсивности за счет дифракции в направлении оси мы наблюдать не будем. Дифракционная картина в плоскости, перпендикулярной оси , будет представлять собой полосы, интенсивность в которых будет зависеть только от координаты .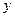

Рис.54.3

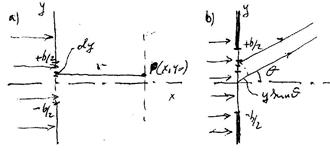
Вычисляя интеграл (54.3), получим

В бесконечных пределах проводится интегрирование по z. Этот интеграл можно вычислить численно для конечной длины щели. Мы же сделаем некоторые упрощения. Для больших , в пределе при 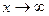для малых углов 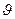можем считать параллельными направления цилиндрических волн от разных полосок 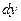в точку наблюдения. Тогда решаемая задача, будет эквивалентна задаче об интерференции волн, излучаемых полосками шириной 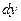, при условии, что разность хода лучей от центральной полоски и произвольной с координатой 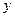будет равна 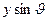(рис.54.3b).

Результирующая напряженность на удаленном экране будет пропорциональна:

,

где введен новый параметр . Интенсивность света в дифракционной картине, в зависимости от параметра , будет равна:

.

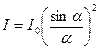Угол 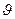, под которым мы будем наблюдать минимум интенсивности в дифракционной картине можно определить из условия 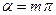, где :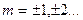

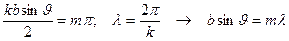. (54.4)

Для нахождения положения максимума необходимо решать трансцендентное уравнение:

,

но для малых 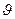можно считать, что максимумы располагаются примерно посередине между минимумами.