ЛЕКЦИЯ 9 Основные задачи математической статистики

2..Определение закона распределения на основе опытных данных.

3. Статическая функция распределения и статический ряд.

4. Числовые характеристики статического распределения.

5. Выравнивание статических рядов.

2.1.3. Задачи и методы обработки опытных данных. а) Основные задачи математической статистики.

Законы распределения случайных величин, как и их числовые характеристики могут быть получены только на основе обработки конкретных опытных данных.

Как уже отмечалось разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, и составляет предмет математической статистики.

Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму. Наиболее часто возникает необходимость в решении следующих трех типов задач.

Задача определения закона распределения случайной величины

по статистическим данным

При обработке значительных по объему статистических данных возникает вопрос об определении законов распределения тех или иных случайных величин. На практике всегда приходится иметь дело с ограниченным количеством экспериментальных данных, в связи с чем результаты наблюдений и их обработки всегда содержат больший или меньший элемент случайности. Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Поэтому к методике обработки экспериментальных данных предъявляют такие требования, чтобы она при сохранении типичных черт явления отбрасывала все второстепенные, связанные с недостаточным объемом опытного материала. В связи с этим возникает задача сглаживания статистических данных и представления их в наиболее компактном виде с помощью соответствующих аналитических зависимостей.

Задача проверки правдоподобия гипотез

Эта задача тесно связана с предыдущей. Статистический материал может с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы: например, согласуются ли результаты эксперимента с гипотезой о распределении случайной величины по конкретному закону . Для решения этого и ряда подобных вопросов в математической статистике существует ряд приемов.

Задача нахождения неизвестных параметров распределения

Довольно часто при обработке статистического материала вопрос об определении законов распределения не возникает. Это может быть связано с недостаточным объемом экспериментального материала, а также в тех случаях, когда закон распределения известен до опыта, из теоретических соображений. Тогда возникает более частная задача по определению некоторых числовых характеристик случайной величины. При небольшом числе опытов эта задача точного решения не имеет. В таких условиях может быть поставлена только задача об определении оценок для искомых параметров, т.е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие.

Рассмотрим последовательно решение 3–х перечисленных задач.

б) Определение закона распределения на основе опытных данных

Статистическая функция распределения

Изучается случайная величина X, закон распределения которой неизвестен, а требуется этот закон определить из опыта. С этой целью над X производится ряд независимых опытов (наблюдений). В каждом из них случайная величина X принимает определенное значение. Совокупность наблюденных значений величины есть первичный статистический материал, подлежащий обработке и исследованию. Такая совокупность называется простым статистическим рядом и оформляется в виде таблицы. в первом столбце которой указан номер опыта, а во втором –соответствующее значение случайной величины.

Простой статистический ряд – это первичная форма записи статистического материала. Он может быть обработан различными способами. Один из них – построение статистической функции распределения случайной величины.

Статистической функцией распределения случайной величины X называется частота события 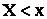в данном статистическом материале:

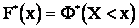(2.19)

Для нахождения значения 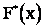достаточно подсчитать число опытов, в которых величина X приняла значения, меньшие чем х, и разделить на общее число произведенных опытов n.

Статистическая функция распределения (рис. 2.14) любой случайной величины (дискретной или непрерывной) представляет собой ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений.

Рис. 2.14

С увеличением числа опытов n 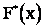сходится по вероятности к .

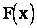Построение 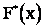в принципе решает задачу описания экспериментального материала. Но при большом числе опытов построение 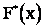рассмотренным способом трудоемко. Кроме того удобнее пользоваться другими характеристиками статистических распределений которые и будут рассмотрены.

Статистический ряд. Гистограмма.

При большом числе наблюдений статистический материал целесообразно представлять в виде статистического ряда . Он строится по следующему алгоритму:

1. Весь диапазон наблюденных значений Х делится на интервалы (разряды), обычно 10–20 интервалов;

2. Подсчитывается количество значений случайной величины. попавших в i-ый разряд (m_i);

3. Находится частота 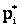, соответствующая данному разряду:

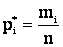
4. Строится таблица, в первой строке которой приведены разряды в порядке их расположения вдоль от абсцисс, а во второй –соответствующие им частоты.

Эта таблица и называется статистическим рядом.

Здесь 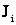– обозначение i-го разряда; 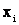, 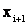– его граница: 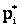– соответствующая частота; к – число разрядов.

Статистический ряд может быть представлен графически в виде так называемой гистограммы . Для ее построения по оси абсцисс откладываются разряды и на каждом из них как на основании строится прямоугольник, площадь которого равна частоте данного разряда. Таким образом, частоту каждого разряда следует поделить на его длину и полученное число взять в качестве высоты прямоугольника (рис. 2.15).

Рис. 2.15

При увеличении числа разрядов к и уменьшении их длины ( ) гистограмма будет все более приближаться к гладкой кривой, являвшейся кривой распределения, т.е. .

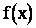Числовые характеристики статистического распределения

Ранее были введены в рассмотрение различные числовые характеристики случайных величин: математическое ожидание, дисперсия, начальные и центральные моменты различных порядков. Аналогичные числовые характеристики существуют и для статических распределений. Каждой числовой характеристике случайной величины X соответствует ее статическая аналогия.

Так, для математического ожидания случайной величины X аналогией является среднее арифметическое наблюденных значений случайной величины:

(2.20)

где 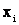– значение случайней величины, наблюденное в i-ом опыте;

n – число опытов.

Аналогичные зависимости существуют и для других числовых характеристик, а именно:

– для статической дисперсии:

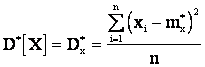(2.21)

– для статистических начальных моментов:

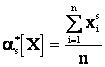(2.22)

– для статистических центральных моментов:

(2.23)

При очень большом количестве опытов вычисление характеристик по формулам (2.20)–(2.23) становится громоздким. В этом случае для статистических числовых характеристик могут быть использованы следующие приближенные формулы:

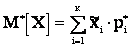(2.20а)

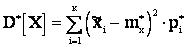(2.21а)

(2.22а)

(2.23а)

где 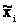– "представитель" i-го разряда;

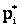– частота i-го разряда;

к – число разрядов.

Следует отметить, что наряду с терминами "статистическое математическое ожидание" (статистическое среднее), "статистическая дисперсия" и т.п., используются для обозначения тех же величин термины "выборочное среднее", "выборочная дисперсия" и т.п.

Выравнивание статистических рядов

Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем. что число наблюдений ограничено, что произведены именно те. а не другие опыты, давшие – именно те, а не другие результаты. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов .

Задача выравнивания заключается в том. чтобы подобрать теоретическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение. Как правило принципиальный вид теоретической кривой заранее известен из соображений, связанных с существом статистического материала. Аналитическое выражение выбранной кривой распределения зависит от определенных параметров. Поэтому задача выравнивания ряда переходит в задачу рационального выбора значений этих параметров таким образом, чтобы соответствие между статистическим и теоретическим распределением было бы наилучшим. Критерии, с помощью которых устанавливается это, могут быть различными: сумма квадратов отклонений теоретической кривой распределения от данных статистического ряда; разность между важнейшими числовыми характеристиками теоретического распределения (моментами) и соответствующими статистическими характеристиками и т.п.