Наброс нагрузки на электродвигатели
Рассмотрим вначале наброс нагрузки на синхронный двигатель, что характерно для двух режимов его работы: снижения питающего напряжения и увеличения момента сопротивления.
Предположим, что произошло резкое снижение напряжения от 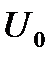 до
до 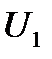 и соответственно изменилась угловая характеристика мощности двигателя (рис. 5.4, а). При этом новый установившийся режим (точка с)наступает после цикла качаний ротора двигателя.
и соответственно изменилась угловая характеристика мощности двигателя (рис. 5.4, а). При этом новый установившийся режим (точка с)наступает после цикла качаний ротора двигателя.
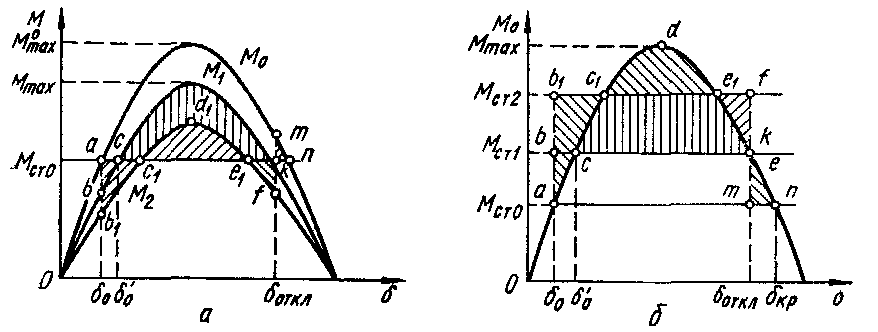
Рис. 5.4. Угловые характеристики мощности синхронного двигателя при уменьшении напряжения (а) и увеличении момента сопротивления (б)
В данном случае площадь ускорения меньше площади торможения, в результате чего система остается устойчивой.
При снижении напряжения до 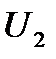 система переходит на характеристику
система переходит на характеристику 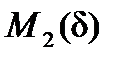 и оказывается неустойчивой. Чтобы сохранить устойчивость, необходимо повысить напряжение до
и оказывается неустойчивой. Чтобы сохранить устойчивость, необходимо повысить напряжение до 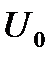 . Для этого, используя метод площадей, надо так подобрать угол δ, чтобы сумма площадей ускорения была меньше суммы площадей торможения:
. Для этого, используя метод площадей, надо так подобрать угол δ, чтобы сумма площадей ускорения была меньше суммы площадей торможения:
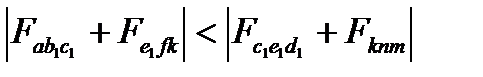 (5.1)
(5.1)
В общем случае снижения напряжения от 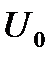 до
до 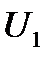 (моментов от
(моментов от 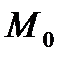 до
до 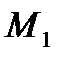 )предельный угол, при котором нужно восстановить напряжение, определяется правилом площадей:
)предельный угол, при котором нужно восстановить напряжение, определяется правилом площадей:
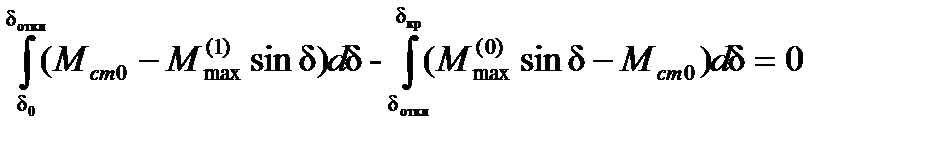 (5.2)
(5.2)
После интегрирования (5.2) получим
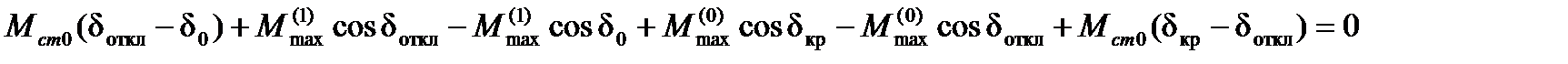
или
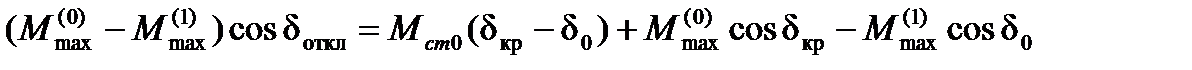
откуда
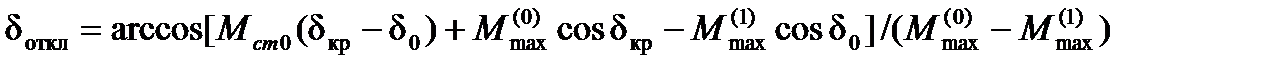 (5.3)
(5.3)
При увеличении нагрузки на валу двигателя процесс протекает следующим образом. Если наброс момента сопротивления происходит от значения 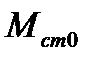 до
до 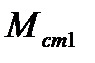 то система будет устойчива, так как площадь ускорения меньше площади торможения (рис. 5.4, б).
то система будет устойчива, так как площадь ускорения меньше площади торможения (рис. 5.4, б).
При увеличении момента до 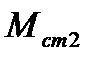 система оказывается неустойчивой, поскольку площадь ускорения
система оказывается неустойчивой, поскольку площадь ускорения 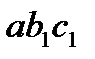 больше площади торможения
больше площади торможения 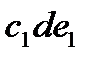 . Для сохранения устойчивости нужно снизить момент от
. Для сохранения устойчивости нужно снизить момент от 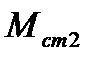 до
до 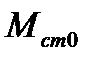 при значении угла δ, не превышающем предельного значения по условию устойчивости.
при значении угла δ, не превышающем предельного значения по условию устойчивости.
В случае наброса момента сопротивления от 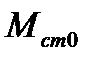 до некоторого значения
до некоторого значения 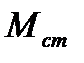 , приводящего к нарушению устойчивости при неизменном питающем напряжении, предельный угол отключения двигателя можно найти из уравнения, составленного по методу площадей:
, приводящего к нарушению устойчивости при неизменном питающем напряжении, предельный угол отключения двигателя можно найти из уравнения, составленного по методу площадей:
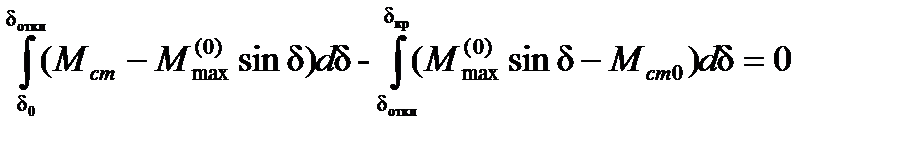 (5.4)
(5.4)
После интегрирования (5.4) и преобразований получим
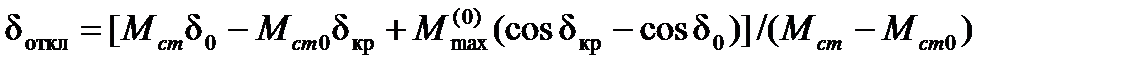 (5.5)
(5.5)
При исследовании устойчивости синхронного двигателя практическое значение имеет предельное время наброса нагрузки на двигатель, работавший в предшествующий момент времени в номинальном или любом другом режиме, т. е. время, в течение которого допустимо понижение питающего напряжения или увеличение момента сопротивления. Это время можно определить, пользуясь методом последовательных интервалов либо упрощенным методом, при котором синусоида аппроксимируется прямой, проходящей через точки угловой характеристики мощности с углами 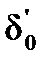 и
и 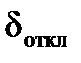 .
.
Предельное время tпр при использовании упрощенного метода (рис. 5.5, а) определяется из уравнения переходного процесса при набросе нагрузки
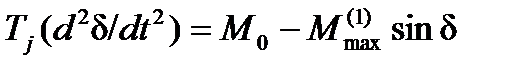 (5.6)
(5.6)
которое после введения новых параметров 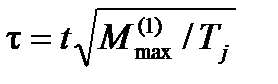 и
и 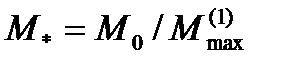
принимает вид
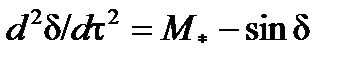 (5.7)
(5.7)
где 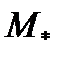 - постоянное значение приведенного момента.
- постоянное значение приведенного момента.
Решение уравнения (5.7) представляет большую трудность, так как синусоидальную функцию 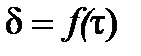 нельзя выразить через конечную комбинацию известных трансцендентных величин.
нельзя выразить через конечную комбинацию известных трансцендентных величин.
Однако его можно проинтегрировать, если синусоиду заменить отрезком прямой 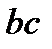 (см. рис. 5.5, а). В этом случае разность между приведенным моментом
(см. рис. 5.5, а). В этом случае разность между приведенным моментом 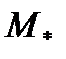 и электромагнитным моментом, равным
и электромагнитным моментом, равным 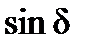 , представляет относительное ускорение
, представляет относительное ускорение 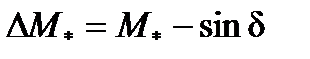 , которое на рис.5.5,аобозначено отрезком 1-2.
, которое на рис.5.5,аобозначено отрезком 1-2.
Заменив участок синусоиды 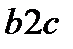 соответствующим отрезком прямой, получим
соответствующим отрезком прямой, получим
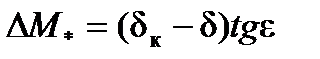 (5.8)
(5.8)
где 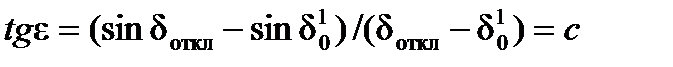
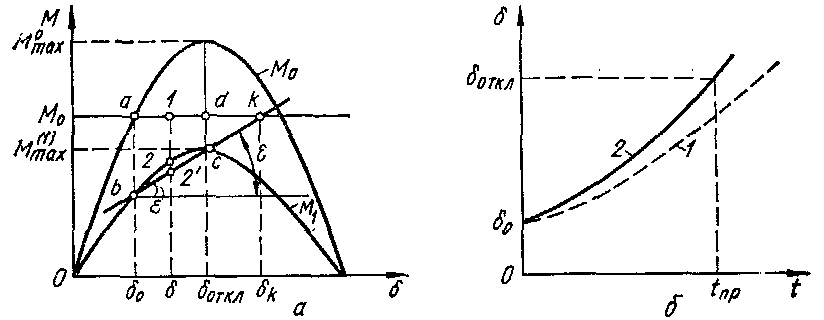
Рис.5.5. Угловые характеристики мощности синхронного двигателя (а) и изменение угла δ при синусоидальной угловой характеристике (кривая 1) и ее аппроксимации прямой (кривая 2)
Таким образом, уравнение (5.7) заменяется уравнением
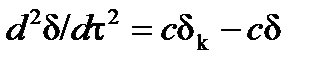 (5.9)
(5.9)
Это уравнение легко интегрируется при начальных условиях 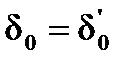 ,
, 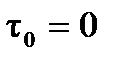 . При этом
. При этом
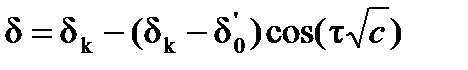 (5.10)
(5.10)
или
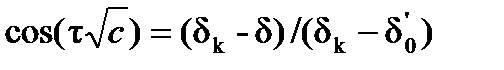
Подставив 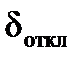 вместо
вместо 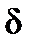 , определим предельное время наброса нагрузки
, определим предельное время наброса нагрузки
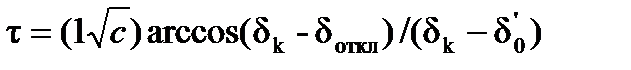 (5.11)
(5.11)
С учетом значений 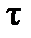 и с, а также замены
и с, а также замены
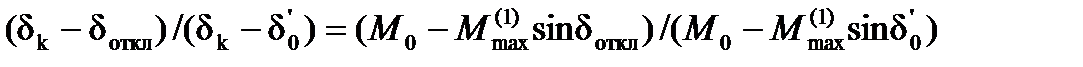
что следует из подобия треугольников 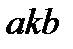 и
и 
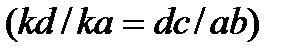 , окончательно запишем
, окончательно запишем
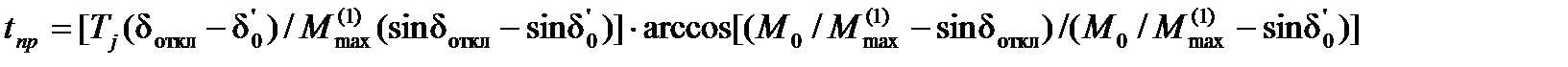 (5.12)
(5.12)
По кривым рис. 5.5, б, характеризующим изменение угла 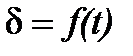 при набросе нагрузки, судят о погрешности аппроксимации синусоиды прямой
при набросе нагрузки, судят о погрешности аппроксимации синусоиды прямой 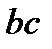 . Таким образом, с приемлемой для инженерных расчетов точностью по формуле (5.12) можно определить допустимое время резкого нарушения режима работы синхронной нагрузки.
. Таким образом, с приемлемой для инженерных расчетов точностью по формуле (5.12) можно определить допустимое время резкого нарушения режима работы синхронной нагрузки.
Рассмотрим теперь влияние сильных возмущений на работу асинхронной нагрузки. При КЗ скольжение асинхронных двигателей увеличивается, в результате чего после отключения КЗ напряжение в системе может не восстановиться до нормального значения. Это обусловлено тем, что с повышением скольжения возрастает потребление реактивной мощности асинхронным двигателем, а при этом снижается напряжение.
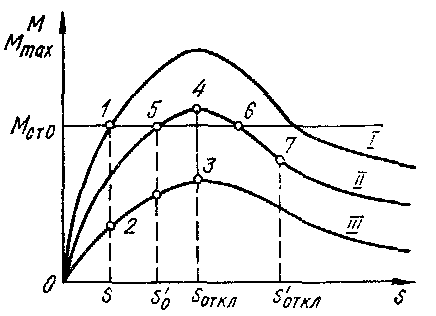
Рис. 5.6. Изменение режима работы асинхронного двигателя при сильных возмущениях
Зависимость электромагнитного момента асинхронного двигателя от скольжения показана на рис. 5.6. При КЗ вращающий момент двигателя резко уменьшается (точка 2 на характеристике III), он начинает тормозиться, а его скольжение возрастает. Если КЗ отключается при скольжении 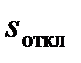 (точка 3 на той же характеристике), то вращающий момент двигателя снова увеличивается. В момент отключения КЗ процесс отражается точкой 4 на характеристике
(точка 3 на той же характеристике), то вращающий момент двигателя снова увеличивается. В момент отключения КЗ процесс отражается точкой 4 на характеристике
II, где вращающий момент больше тормозного. Двигатель ускоряется, его скольжение падает, и возникает новый установившийся режим (точка 5 на характеристике I),
Если длительность КЗ велика и оно отключается при скольжении 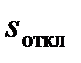 (за точкой 6 на характеристикеII), то увеличение вращающего момента двигателя после отключения повреждения может оказаться недостаточным. Избыточный момент при этом становится тормозящим. Скольжение двигателя возрастает, и он останавливается.
(за точкой 6 на характеристикеII), то увеличение вращающего момента двигателя после отключения повреждения может оказаться недостаточным. Избыточный момент при этом становится тормозящим. Скольжение двигателя возрастает, и он останавливается.
При набросах нагрузки на асинхронный двигатель, вызывающих уменьшение питающего напряжения или увеличение момента на валу, скольжение двигателя повышается. Если при этом момент сопротивления окажется большим, чем максимальный 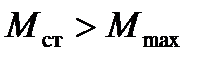 , то скольжение двигателя возрастает до значения s = 1, и он остановится. Чтобы этого не произошло, нужно своевременно восстановить напряжение или уменьшить момент на валу двигателя.
, то скольжение двигателя возрастает до значения s = 1, и он остановится. Чтобы этого не произошло, нужно своевременно восстановить напряжение или уменьшить момент на валу двигателя.
В нормальном режиме асинхронный двигатель работает при скольжении s0 и моменте 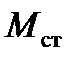 (точка а на рис. 5.7, а).Предположим, что напряжение на зажимах двигателя снизилось с
(точка а на рис. 5.7, а).Предположим, что напряжение на зажимах двигателя снизилось с 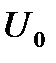 до
до 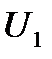 .При этом электромагнитный момент двигателя уменьшится в
.При этом электромагнитный момент двигателя уменьшится в 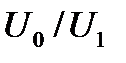 раз:
раз:
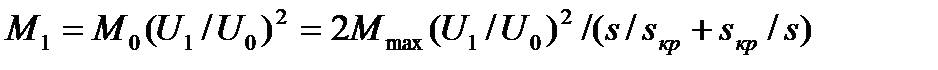 (5.13)
(5.13)
При снижении электромагнитного момента с 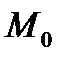 до
до 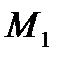 двигатель будет тормозиться и остановится. Время, по истечении которого двигатель остановится, и изменение скольжения за это время можно найти, если проинтегрировать уравнение движения двигателя
двигатель будет тормозиться и остановится. Время, по истечении которого двигатель остановится, и изменение скольжения за это время можно найти, если проинтегрировать уравнение движения двигателя
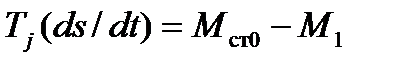 (5.14)
(5.14)
При этом возникает задача определения предельного времени, в течение которого может снижаться напряжение с 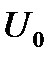 до
до 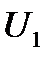 без останова двигателя с продолжением его работы после восстановления напряжения. Для этого скольжение не должно превышать значения, большего чем
без останова двигателя с продолжением его работы после восстановления напряжения. Для этого скольжение не должно превышать значения, большего чем 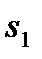 (точка
(точка 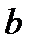 на рис. 5.7, а), поскольку при
на рис. 5.7, а), поскольку при 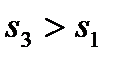 двигатель переходит на неустойчивую часть характеристики, и восстановление питающего напряжения уже не сможет прекратить его торможения и останова.
двигатель переходит на неустойчивую часть характеристики, и восстановление питающего напряжения уже не сможет прекратить его торможения и останова.
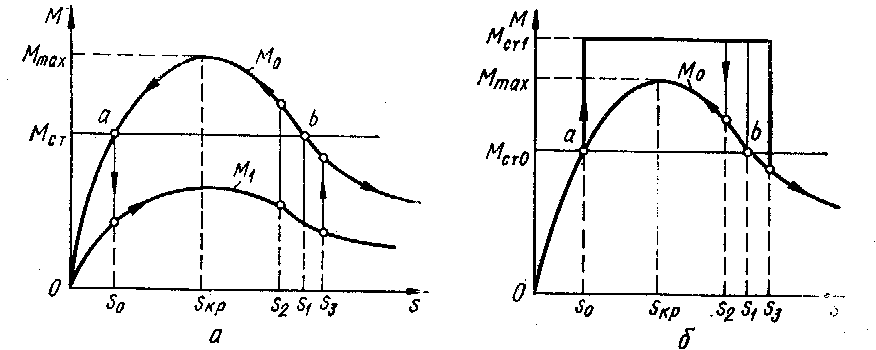
Рис. 5.7. Механические характеристики асинхронного двигателя при снижении питающего напряжения (а) и повышении момента сопротивления (б)
Подставив (5.13) в уравнение (5.14), последнее можно записать в виде
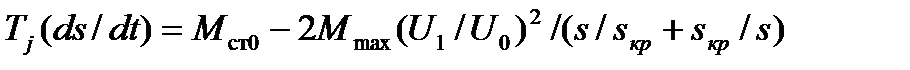
откуда
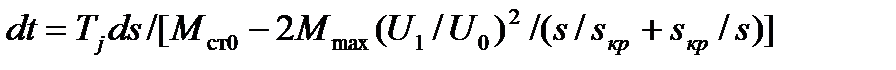
После интегрирования левой части этого уравнения от 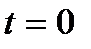 до
до 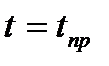 а правой от
а правой от 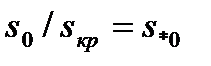 до
до 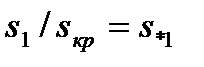 определим время, при котором двигатель достигает скольжения
определим время, при котором двигатель достигает скольжения  :
:
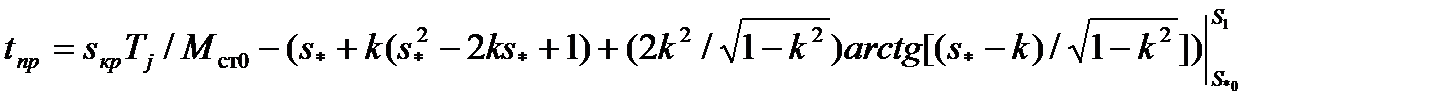 (5.15)
(5.15)
где
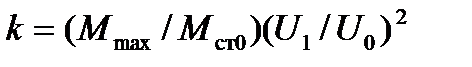 ;
; 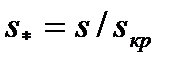
Значения 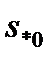 и
и 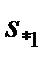 найдем из выражения
найдем из выражения
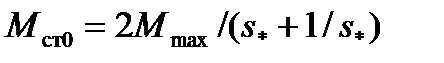 или
или 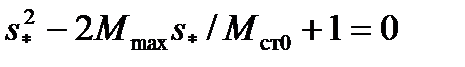
откуда
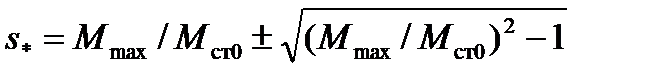 (5.16)
(5.16)
Знак «+» здесь соответствует 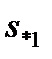 , а знак «— » -
, а знак «— » - 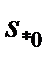 .
.
Поведение двигателя при повышении момента сопротивления на валу (рис. 5.7, б)полностью соответствует его поведению при снижении питающего напряжения, но при расчете 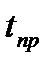 по формуле (5.15)
по формуле (5.15) 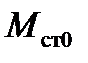 нужно заменить на
нужно заменить на 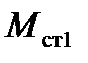 .
.
Дата добавления: 2015-12-08; просмотров: 4400;
