Статическая устойчивость

Из рассмотрения простейших механических систем следует, что естьсостояния (режимы), в которых системы после случайного возмущения стремятся восстановить исходный или близкий к нему режим (рис.6). В других режимах случайное возмущение уводит системы от исходного состояния. В первом случае системы являются устойчивыми, во втором — неустойчивыми.

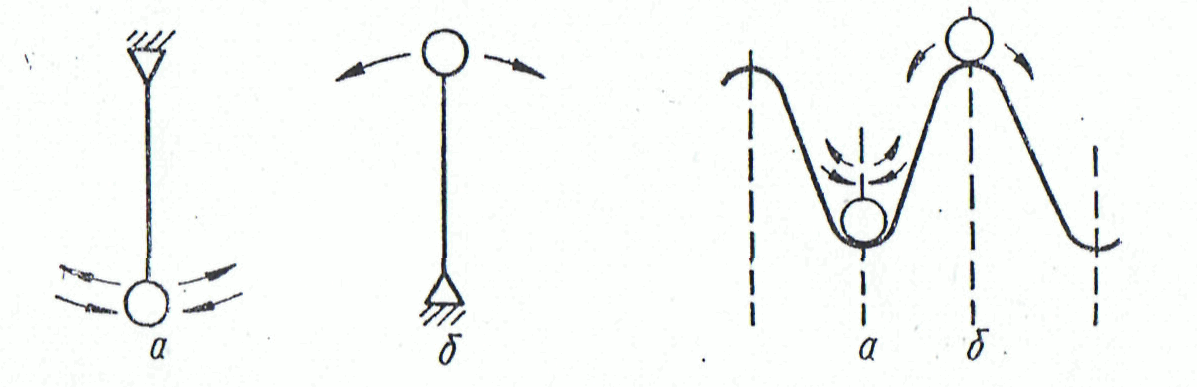
Рис.6. Устойчивые (а) и неустойчивые (б) состояния равновесия механических систем

В установившемся режиме между энергией источника W_Г, поступающей в систему извне, и энергией, расходуемой в нагрузке и на покрытие потерь, имеется баланс. При каком-либо возмущении, проявляющемся в изменении параметра режима П на 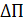, этот баланс нарушается.

Если система обладает такими свойствами, что энергия

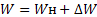> 9

после возмущения расходуется более интенсивно, чем приобретается от внешнего источника 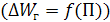, то новый режим, возникший в результате возмущения, не может быть обеспечен энергией и в системе должен восстановиться прежний установившийся или близкий к нему режим. Такая система устойчива.

Из определения устойчивости следует, что условием сохранения устойчивости системы (критерием устойчивости) является соотношение

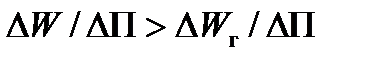(10)

или в дифференциальной форме

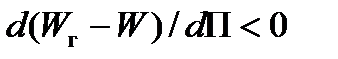(11)

Величину 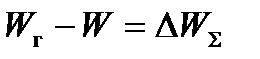называют избыточной энергией. Эта энергия положительна, если дополнительная генерируемая энергия, появившаяся при возмущении, возрастает интенсивнее, чем нагрузка системы с учетом потерь в ней. При этом условии критерий устойчивости запишется в виде

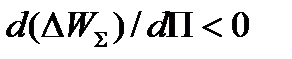(12)

т. е. режим устойчив, если производная от избыточной энергии по определяющему параметру П отрицательна.

Для обеспечения статической устойчивости системы существенное значение имеет запас статической устойчивости, который определяет допустимые пределы ухудшения режима до нарушения статической устойчивости. Запас статической устойчивости может характеризоваться углами сдвига роторов генераторов и напряжениями в узловых точках системы.

Большое значение имеет наличие запаса статической устойчивости в послеаварийном режиме, который уменьшается по сравнению с запасом статической устойчивости в нормальном режиме, причем в последнем запас устойчивости по увеличению мощности электрической передачи должен составлять 15 — 20 %, а в после-аварийном режиме 5 — 10 %, но эти значения строго не лимитируются.

Чтобы проверить статическую устойчивость системы, необходимо составить дифференциальные уравнения малых колебаний для всех ее элементов и регулирующих устройств, а затем исследовать корни характеристического уравнения на устойчивость. Поскольку строгое решение такой задачи очень сложно, в инженерных расчетах применяются приближенные методы исследования устойчивости, которые основываются на использовании практических критериев устойчивости.

Рассмотрим простейшую схему электрической передачи, в которой генератор работает через трансформатор и линию на шины неизменного напряжения, т. е. на шины системы, мощность которой настолько велика по сравнению с мощностью рассматриваемой электрической передачи, что напряжение на ее шинах можно считать неизменным по амплитуде и фазе при любых режимах (рис.7, а).

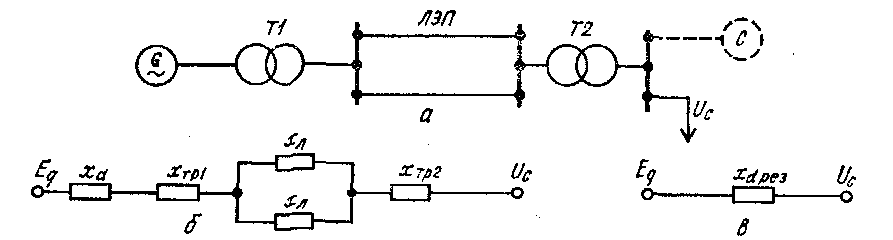
Рис.7. Схема электропередачи (а) и схемы ее замещения (б, в)

При исследовании характера переходного процесса удобно пользоваться угловой характеристикой 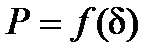, где 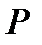-электромагнитная мощность генератора; δ - угол сдвига по фазе между синхронной э. д. с. генератора E_q и напряжением на шинах приемной системы U_с.

Из схем замещения рассматриваемой электропередачи (рис.7, б, в)следует, что результирующее сопротивление

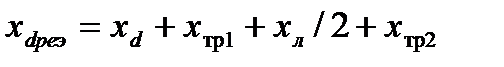(13)

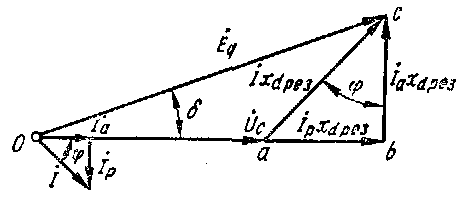
Рис.8. Векторная диаграмма для нормального режима работы электропередачи

Векторная диаграмма для нормального режима работы этой электропередачи показана на рис.8, откуда видно, что 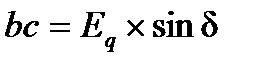, или 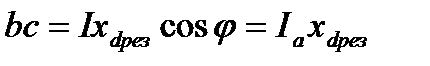. При этом

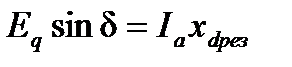(14)

Умножив обе части равенства (14) на 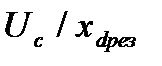, получим активную мощность, передаваемую приемной системе:

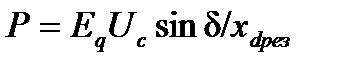(15)

где

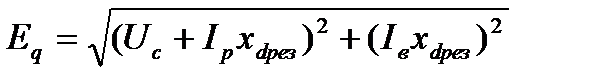
или

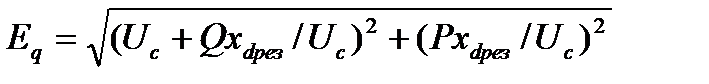
Из выражения (15) следует, что при постоянстве э. д. с. генераторов Е_q и напряжения на шинах приемной системы U_c изменение передаваемой мощности Р зависит лишь от изменения угла δ.

Мощность, отдаваемую генератором в сеть, можно изменить также воздействием на регулирующие клапаны турбины. В исходном режиме мощность турбины уравновешивается мощностью генератора, работающего с неизменной частотой вращения. По мере открытия регулирующих клапанов (или направляющего аппарата у гидротурбин) мощность турбины возрастает, в результате чего равновесие вращающего и тормозящего моментов турбины и генератора нарушается, что вызывает ускорение вращения генератора.

При ускорении генератора вектор э. д. с. 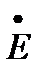перемещается относительно вращающегося с неизменной скоростью вектора напряжения приемной системы 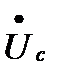. Связанное с этим увеличение угла δ приводит к соответствующему повышению мощности генератора по синусоидальному закону до тех пор, пока она вновь не уравновесит возросшую мощность турбины. Поскольку зависимость 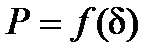носит синусоидальный характер, с увеличением угла δ мощность Р сначала возрастает, а затем, достигнув максимального значения, начинает падать.

При заданных значениях э. д. с. генератора E_q и напряжения приемника U_c существует определенный максимум передаваемой мощности, который называется идеальным пределом мощности. Он наступает при δ = 90° и определяется выражением

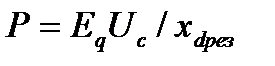(16)

Графическая зависимость активной мощности Р от угла δ показана на рис. 9.

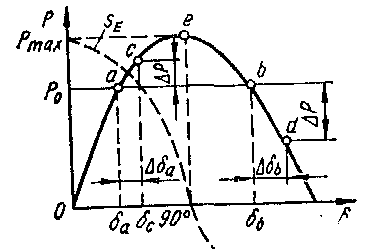
Рис.9. Угловая характеристика и характеристика синхронизирующей мощности генератора

В установившемся режиме мощность турбины Р₀ равна мощности генератора Р, т. е. между неизменной мощностью первичного двигателя и мощностью генератора существует равновесие. При этом каждому значению мощности турбины Р₀ соответствует две точки равновесия на угловой характеристике мощности генератора (см. рис.9) и, следовательно, два значения угла (δ_а и δ_b).

Однако устойчивый режим работы возможен лишь в точке а, что легко показать, рассмотрев характер движения ротора генератора при небольшом отклонении от точек равновесия (рис.10).

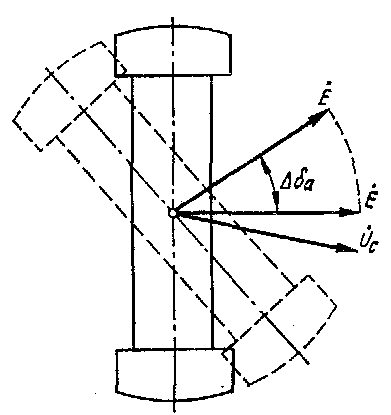
Рис.10. Изменение положения ротора генератора при малом возмущении

Предположим, что вследствие небольшого возмущения угол δ_а увеличился на Δδ_а. Этому случаю соответствуют переход рабочей точки на угловой характеристике из а в с и увеличение мощности генератора на ΔP т. е. положительному приращению угла соответствует положительное приращение мощности.

В результате увеличения мощности генератора при неизменной мощности турбины равновесие вращающего и тормозящего моментов турбины и генератора нарушается, и на валу машины возникает тормозящий момент. Под его влиянием ротор генератора начинает замедляться, что обусловливает перемещение связанного с ротором вектора э. д. с. генератора 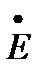сторону уменьшения угла δ. С уменьшением угла δ вновь восстанавливается исходный режим в точке а. Следовательно, данный режим системы является устойчивым. К этому же выводу можно прийти и при отрицательном приращении угла Δδ в точке а.

В точке b на рис.9 положительное приращение угла Δδ сопровождается отрицательным изменением мощности генератора ΔР. Уменьшение мощности генератора вызывает появление ускоряющего момента, под влиянием которого угол δ не уменьшается, а возрастает. С увеличением угла δ мощность генератора продолжает падать, что обусловливает дальнейшее увеличение угла δ и т, д. Процесс протекает прогрессивно и генератор выпадает из синхронизма, т. е. режим работы в точке b статически неустойчив.

Таким образом, состояние генератора, соответствующее точке а и любой другой точке на возрастающей части синусоидальной характеристики мощности, статически устойчиво, а состояние генератора, соответствующее всем точкам спадающей части характеристики, статически неустойчиво. Отсюда вытекает следующий критерий статической устойчивости системы:

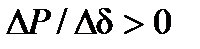
или

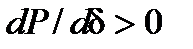(17)

Из (17) следует, что статическая устойчивость системы обеспечивается, если приращения угла δ и мощности генератора Р имеют один и тот же знак.

Производную 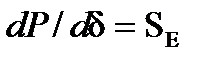принято называть синхронизирующей мощностью. Эта мощность характеризует реакцию генератора на увеличение угла сдвига ротора. Положительный знак ее является критерием статической устойчивости. Если АРВ отсутствует, то синхронизирующая мощность определяется выражением

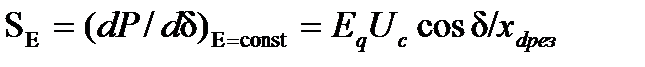(18)

При δ <90° синхронизирующая мощность положительна и обеспечиваются устойчивые стационарные режимы работы системы (см. рис.9). Количественно статическая устойчивость характеризуется коэффициентом запаса

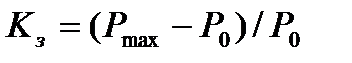
где Р_max и P₀ – максимальная и номинальная мощности системы.