Лекция 14. Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна. Возбужденный атом по истечении некоторого времени освобождается от излишка энергии с помощью испускания фотона
Правила отбора
Возбужденный атом по истечении некоторого времени освобождается от излишка энергии с помощью испускания фотона. Это излучательные переходы. Существуют также безызлучательные переходы. Поэтому можно говорить о среднем времени жизниатома в возбужденном состоянии. Переходы возбужденных атомов с излучением происходят «сами собой». Это спонтанные, или самопроизвольные переходыХарактерное время жизни атома в возбужденном состоянии  с.
с.
Существуют также вынужденные переходы, которые происходят под действием внешнего поля. В этом случае атомы поглощаютэнергию поля или вынужденно излучают, переходя в состояние с меньшей энергией. Вероятность того, что в момент времени t атом будет находиться в этом состоянии, определяется величиной 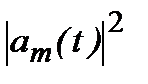 , которая таким образом характеризует вероятность перехода из состояния n в состояние m. С такими вероятностями связаны коэффициенты Эйнштейна.
, которая таким образом характеризует вероятность перехода из состояния n в состояние m. С такими вероятностями связаны коэффициенты Эйнштейна.
Рассмотрим два состояния атома с энергиями 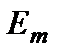 и
и 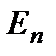 (при
(при  ) Вводится вероятность спонтанного перехода в единицу времени
) Вводится вероятность спонтанного перехода в единицу времени  из состояния
из состояния 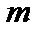 в состояние
в состояние 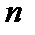 . Величина
. Величина 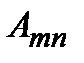 имеет смысл среднего числа актов излучения в единицу времени, приходящихся на один атом. В момент времени
имеет смысл среднего числа актов излучения в единицу времени, приходящихся на один атом. В момент времени 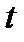 в состоянии
в состоянии 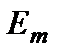 находится
находится 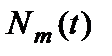 атомов. За время
атомов. За время 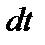 произойдет
произойдет  переходов в состояние
переходов в состояние 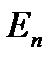 . Величина
. Величина 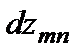 определяет уменьшение числа атомов, находившихся в момент времени
определяет уменьшение числа атомов, находившихся в момент времени  в состоянии
в состоянии 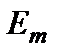 :
: 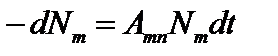 . Решение этого уравнения:
. Решение этого уравнения: 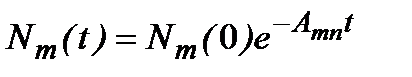 . (2.76)
. (2.76)
Величину 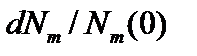 есть мера вероятности спонтанного перехода атомов за время dt. Среднее время такого перехода
есть мера вероятности спонтанного перехода атомов за время dt. Среднее время такого перехода 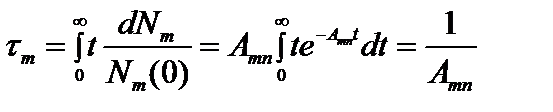 .(2.77)
.(2.77)
Таким образом, 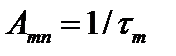 . Интенсивность излучения согласно (2.76) уменьшается со временем по закону:
. Интенсивность излучения согласно (2.76) уменьшается со временем по закону:  . (2.77а)
. (2.77а)
Если атом, находящийся в состоянии 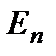 , помещен во внешнее электромагнитное поле с частотой
, помещен во внешнее электромагнитное поле с частотой 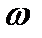 , то он поглощает энергию поля при совпадении этой частоты с
, то он поглощает энергию поля при совпадении этой частоты с  и переходит в возбужденное состояние
и переходит в возбужденное состояние 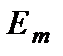 . Пусть
. Пусть 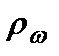 – спектральная плотность энергии электромагнитного излучения. Вводят величину
– спектральная плотность энергии электромагнитного излучения. Вводят величину  .(2.78)Это - вероятность поглощения излучения атомом в единицу времени.
.(2.78)Это - вероятность поглощения излучения атомом в единицу времени.
Существует обратный процесс – вынужденное, стимулированное,или индуцированное испусканиепри переходе  под воздействием внешнего электромагнитного поля, частота которого равна частоте перехода. Такой процесс характеризуется величиной
под воздействием внешнего электромагнитного поля, частота которого равна частоте перехода. Такой процесс характеризуется величиной 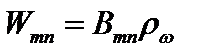 . (2.78а)
. (2.78а)
Это - вероятность индуцированного излучения в единицу времени. 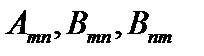 - коэффициенты Эйнштейна. Коэффициенты Эйнштейна связаны соотношениями:
- коэффициенты Эйнштейна. Коэффициенты Эйнштейна связаны соотношениями: 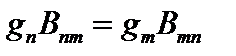 ,
, 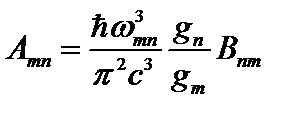 . Коэффициент
. Коэффициент 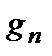 (или
(или 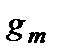 ) - статистический вес, или кратность вырождения
) - статистический вес, или кратность вырождения 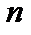 -го (или
-го (или 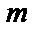 -го) состояния.
-го) состояния.
Квантовое число 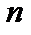 , определяющее состояния осциллятора, при переходах может изменяться лишь на ±1:
, определяющее состояния осциллятора, при переходах может изменяться лишь на ±1: 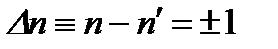 . (2.85)
. (2.85)
Частота перехода равна частоте классического осциллятора: 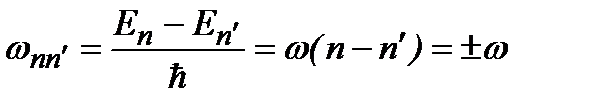 ,
,
Состояния квантового ротатора описываются квантовыми числами 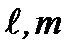 . При переходах из состояния
. При переходах из состояния 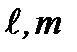 в состояние
в состояние 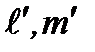 правила отбора: для изменения орбитального квантового числа:
правила отбора: для изменения орбитального квантового числа:  , (2.86)
, (2.86)
для изменения магнитного квантового числа: 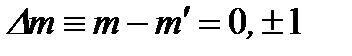 . (2.87)
. (2.87)
Эти правила определяют также поляризацию излучения.
Возможные изменения состояний ротатора связаны с законом сохранения четности. Инверсии 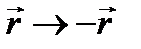 в сферической системе координат (
в сферической системе координат ( 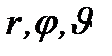 ) соответствует преобразование:
) соответствует преобразование:
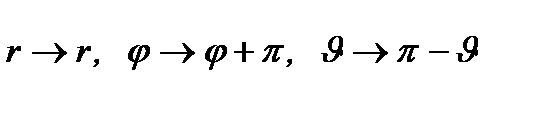 . (2.89)
. (2.89)
волновая функция при инверсии преобразуется по закону: 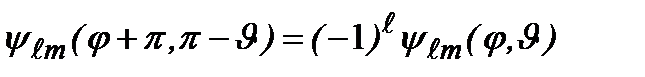 .
.
Отсюда следует, что четность состояний ротатора определяется значением орбитального квантового числа 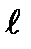 . Если
. Если  – четное число, то состояние четно. Если
– четное число, то состояние четно. Если  – нечетное число, то состояние – нечетно.
– нечетное число, то состояние – нечетно.
Таким образом, возможны переходы  лишь между состояниями с различной четностью.Это – правило Лапорта. Так как четность определяется значениями орбитального квантового числа, то отсюда следует правило (2.86). Дипольные переходы при
лишь между состояниями с различной четностью.Это – правило Лапорта. Так как четность определяется значениями орбитального квантового числа, то отсюда следует правило (2.86). Дипольные переходы при  или
или 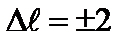 являются запрещенными.
являются запрещенными.
Правило отбора при квадрупольных переходах: 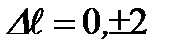 . При этом переходы с
. При этом переходы с 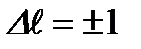 запрещены.
запрещены.
Дата добавления: 2015-12-08; просмотров: 642;
