Перпендикулярность плоскостей

Две плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой. Но через прямую линию (перпендикуляр) в пространстве можно провести множество плоскостей перпендикулярных данной.

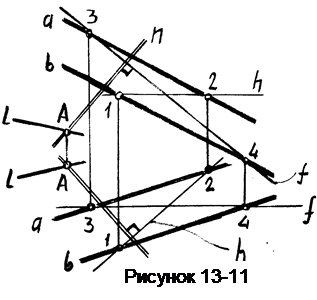Пример 7. Провести через т.А плоскость Б, перпендикулярную заданной плоскости Д(а//b), (рисунок 13-11).

Сначала проведем через т.А прямую n перпендикулярно плоскости Д, для чего на ней предварительно проводим горизонталь и фронталь.

Затем через т.А проводим произвольную прямую l.

Эти две прямые n и l задают одну из плоскостей перпендикулярных плоскости Д.

Пример 8. Определить, перпендикулярны ли данные плоскости Б(а//b)и Д(f∩h), (рисунок 13-12).

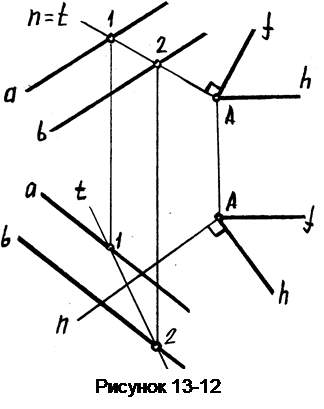Из точки пересечения горизонтали h и фронтали f проводим прямую n перпендикулярно плоскости Б.

Проверим принадлежность прямой n плоскости Б. Если плоскости перпендикулярны, то нормаль n будет либо принадлежать, либо будет параллельна плоскости Б.

В нашем случае прямая n не принадлежит и не параллельна этой плоскости (о чем можно судить по расположению проекций n и t на видах), следовательно плоскость Б не перпендикулярна плоскости Д.

Пример 9. Через прямую l провести плоскость Д перпендикулярно плоскости Б (А, b) (рисунок 13-13).

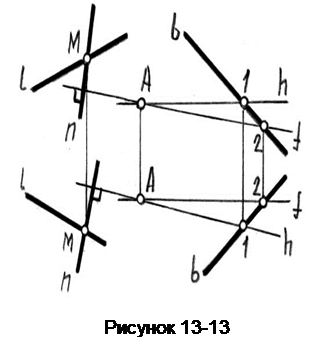На прямой l берем произвольную точку М и через неё проводим прямую n перпендикулярно плоскости Б. Пересекающиеся прямые lи nзадают искомую плоскость.