Параллельность и перпендикулярность прямой и плоскости.
Прямая относительно плоскости может занимать следующие положения:
- лежать в плоскости;
- быть ей параллельна;
- пересекать плоскость.
Перпендикулярность прямой и плоскости
Условие перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.
Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.
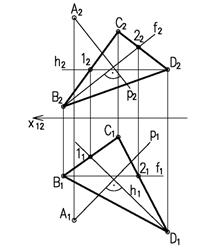На рисунке 1.8 через точку А(А1;А2) проведена прямая, перпендикулярная плоскости 
(∆ВСD).
В плоскости ά проведены горизонталь h (h1,h2) и фронталь f (f1,f2) , затем через А1 проведена горизонтальная проекция перпендикуляра p1 под прямым углом к h1, а через точку А2 фронтальная проекция перпендикуляра p2 под прямым углом к f2. Прямые p1 и p2 есть проекции искомого перпендикуляра р.
р ┴ ά → (p1 ┴ h1)+ (p2 ┴ h2)
Дата добавления: 2015-09-18; просмотров: 883;