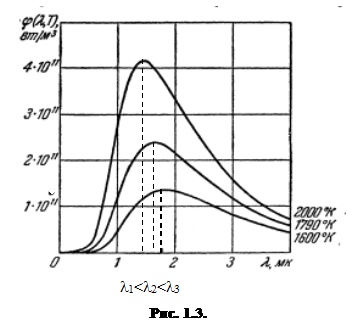
Распределение энергии в спектре излучения абсолютно черного тела.

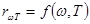Согласно закону Кирхгофа испускательная способность абсолютно черного тела , где T – температура стенок полости. Если температуру стенок полости поддерживать постоянной и равной T, то из отверстия вышеописанной полости выходит излучение весьма близкое по спектральному составу к излучению абсолютно черного тела при той же температуре. Разлагая это излучение в спектр (например, при помощи дифракционной решетки) и измеряя балометром интенсивность различных участков спектра, можно найти экспериментально вид функци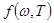и или 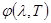(рис.1.3.).

Разные кривые относятся к разным значениям температуры абсолютно черного тела. Площадь, охватываемая кривой дает энергетическую светимость абсолютно черного тела при соответствующей температуре.

Анализ этих кривых позволяет сделать следующие выводы:

1) Спектр излучения абсолютно черного тела имеет сплошной характер, т.е. в спектре этого излучения представлен непрерывный ряд длин волн.

2) Существует отчетливо выраженный максимум излучательной способности и с повышением температуры этот максимум смещается в сторону более коротких длин волн.

3) Излучательная способность абсолютно черного тела уменьшается в сторону коротких длин волн более резко, чем в сторону более длинных волн.

Законы излучения.

Теоретическое объяснение излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к открытию квантов энергии. Посмотрим, как это происходило исторически.

1) Закон Стефана[b] - Больцмана[c]. Долгое время многочисленные попытки получить теоретически вид функции 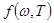не давали общего решения задачи.

Стефан (1879г.), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость любого тела R_э~T⁴ (~ четвертой степени абсолютной температуры).

Больцман (1884г.), исходя из термодинамических соображений, получил для абсолютно черного тела соотношение:

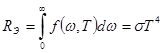- которое известно под названием закона Стефана-Больцмана.

ОПРЕДЕЛЕНИЕ: Закон Стефана-Больцмана: полная лучеиспускающая способность (энергетическая светимость) абсолютно черного тела пропорциональна четвертой степени абсолютной температуры.

s - постоянная Стефана-Больцмана. s=5,7×10^-8Вт/(м²×град⁴).

2) Закон Вина. Вин[d] (1893г.), воспользовавшись кроме термодинамики, электромагнитной теорией, показал, что функция спектрального распределения должна иметь вид:

.

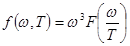На основании этого он вывел следующие законы:

ОПРЕДЕЛЕНИЕ: Закон смещения Вина: длина волны, на которую приходится максимум излучательной способности обратно, пропорциональна абсолютной температуре:

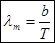
b=2,9×10³мк×К – 1^ая постоянная Вина.

ОПРЕДЕЛЕНИЕ: Максимальная излучательная способность абсолютно черного тела r_wmax возрастает пропорционально пятой степени абсолютной температуры:

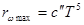
с²=1,3×10^-3Вт/м²×К⁵ – 2^ая постоянная Вина.

На законе Вина основан метод определения температуры раскаленных тел (оптическая пирометрия) по спектру их излучения. Именно этим методом впервые была определена температура поверхности Солнца. Максимум энергии солнечного излучения приходится на длину волны l_m=0,47мкм. Следовательно, абсолютная температура поверхности Солнца равна .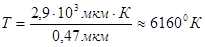

3) Рэлей и Джинс[e] сделали попытку определить функцию 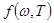, исходя из теоремы классической статистики о равномерном распределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT: одна половинка на электрическую, а другая на магнитную энергию волны. Предположив также, что в некоторой полости излучение представляет собой систему стоячих волн, они получили, что

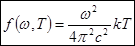- формула Рэлея-Джинса.

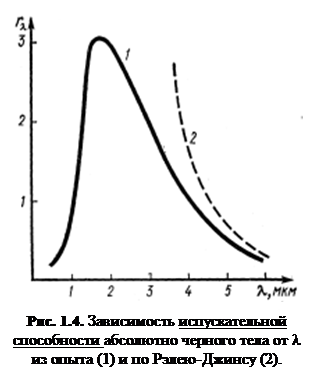
Оказывается, что формула Рэлея-Джинса, вывод которой безупречен с классической точки зрения (он основан на применении законов термодинамики и теоремы Больцмана о равнораспределении энергии по степеням свободы) удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн и резко расходится с опытом для малых длин волн. Интегрирование выражения, представляющего формулу Рэлея-Джинса, по w от 0 до ¥ дает для равновесной плотности энергии (также как и для энергетической светимости R_э) бесконечно большие значения (рис.1.4.). Эти расхождения теории и эксперимента, обнаруженные на рубеже XIX и XX веков, получили название ультрафиолетовой катастрофы.

Посмотрим, как удалось разрешить сложившееся противоречие.

Расхождения теории и эксперимента явились серьезным предостережением, выходящим далеко за рамки задачи о построении универсальной функции 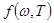. Расхождение формулы Рэлея-Джинса с экспериментом указывало на существование каких-то закономерностей, несовместимых с представлениями классической статистической физики и электродинамики. Смысл общего вывода заключается в том, что вся классическая физика имеет определенные границы применимости и использование ее законов и методов вне границ приводит к противоречию с опытом, являющимся основным критерием правильности той или иной теории.

Формула Планка.

В 1900г. Планку удалось найти вид функции 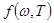в точности, соответствующий опытным данным. Но для этого ему пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии e (квантов), величина которых пропорциональна частоте излучения. А именно: 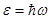. Здесь 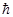- постоянная Планка, 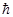=1,054×10^-34Дж×с. 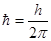, поэтому h=6,62×10^-34Дж×с.

В основе рассуждений, приводящих к определенному Планком виду функции спектрального распределения 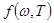, лежит выражение для средней энергии излучения с частотой w, которая вычисляется согласно следующей формуле:

(*)

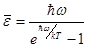Если бы энергия могла принимать непрерывный ряд значений, то ее среднее значение было бы равно 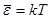. В этом можно убедиться, положив 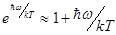, что выполняется тем точнее, чем меньше 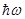(т.е., чем больше l).

Заменив в формуле Рэлея-Джинса kT выражением (*), получим формулу, найденную Планком:

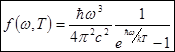
Получим выражение для средней энергии излучения частоты w, исходя из представлений Планка об испускании электромагнитного излучения в виде квантов энергии.

Если излучение испускается квантами (порциями) 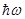, то энергия e_n должна быть кратной этой величине, т.е.

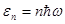, (n=0, 1, 2, 3,…).

Согласно закону Больцмана вероятность P_n того, что энергия излучения имеет величину e_n, определяется выражением:

.

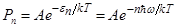Нормировочный множитель A можно найти, исходя из условия, что сумма всех P_n должна быть равна единице. Действительно, сумма P_n представляет собой вероятность того, что энергия имеет одно из возможных для нее значений. Такое событие является достоверным и, следовательно, имеет вероятность, равную единице. Итак, .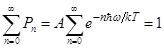

Тогда, найдя значение A, получим, что .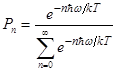

Предположив возможность измерения значения энергии данной спектральной составляющей излучения в любой момент времени, произведем через равные промежутки времени очень большое число таких измерений N. Разделив сумму полученных значений на число измерений N, найдем среднее по времени значение энергии 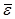. При очень большом N количество измерений N_n, которые дадут результат e_n, будет равно NP_n. Поэтому

.

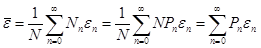Следовательно, среднее значение энергии излучения частоты w будет определяться следующим выражением:

.

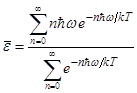Дальнейшие вычисления легко провести, приняв, что 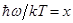, тогда

.

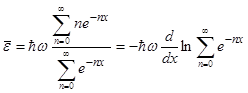Выражение, стоящее под знаком логарифма, представляет собой сумму членов бесконечной убывающей геометрической прогрессии с первым членом, равным единице и знаменателем прогрессии, равным 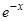. Поэтому по известной из алгебры формуле 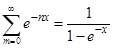. Учитывая этот результат, имеем после дифференцирования

.

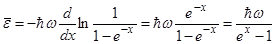Наконец, заменив x его значением 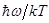, получим окончательное выражение для средней энергии излучения частоты w:

.

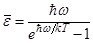Переходя к длинам волн формулу Планка можно записать в виде:

.

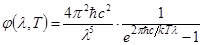Заметим, что при выполнении условия 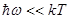квантовая формула Планка переходит в классическую формулу Рэлея-Джинса. Следовательно, условие малости кванта энергии 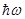по сравнению с величиной 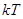определяет границы применимости классической теории. Если нельзя считать 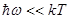, то использование формулы Рэлея-Джинса незаконно и для описания свойств теплового излучения нужно применять формулу Планка.

Применим формулу Планка для вывода законов Стефана-Больцмана и закона смещения Вина.

1) Энергетическая светимость абсолютно черного тела R_э:

.

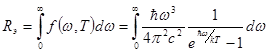Пусть 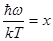, тогда 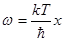и 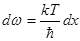. Сделав такую замену, получаем: 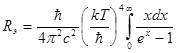. Значение интеграла 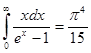, поэтому 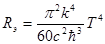. Обозначив 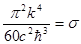, получаем закон Стефана-Больцмана: 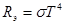. А подставив в формулу числовые значения для p, k, c, 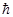, получаем, что s=5,6696×10^-8Вт/(м²×град⁴), что очень хорошо согласуется с экспериментальным значением.

2) Для вывода закона смещения Вина воспользуемся связью между функциям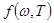и и .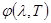

Участку спектра dw соответствует интервал длин волн dl. Определяющие один и тот же участок спектра величина dw и dl связаны простым соотношением, вытекающим из формулы: 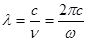. Дифференцирование дает 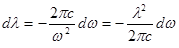. Знак “-“ можно не учитывать в дальнейших вычислениях, он лишь указывает, что с возрастанием l частота w убывает и наоборот.

Если интервалы dw и dl относятся к одному и тому же участку спектра, то величины dR_э и dR_l должны совпадать, т.е.

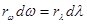
или

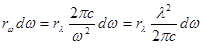(D)

Для абсолютно черного тела 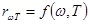, тогда аналогично формуле (D) получаем 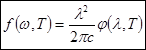- формулу связи функци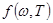й и .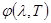

Отсюда 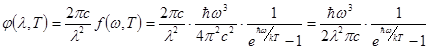. Видно, что функция 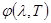зависит от l и от w. Выразим эту функцию через l, учтя, что .

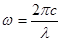Тогда имеем

.

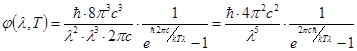Далее возьмем первую производную функции 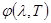по l и приравняем ее нулю (условие экстремума).

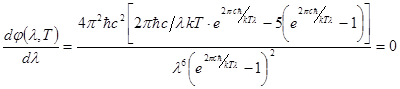
Удовлетворяющие этому уравнению значения l=0 и l=¥ соответствуют минимуму функции 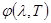. Значение l_m, при котором функция достигает максимума, обращает в нуль выражение, стоящее в числителе в квадратных скобках. Обозначим 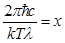, получим уравнение: .

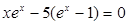Решение этого трансцендентного уравнения дает значение x=4,965. Следовательно, 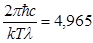. Откуда 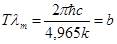- закон смещения Вина. Подстановка числовых значений p, c, k, 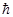дает значение для b=2,9×10³(мкм×К).

Таким образом, формула Планка дает исчерпывающее описание равновесного теплового излучения.

САМОСТОЯТЕЛЬНО: Оптическая пирометрия, Типы пирометров: радиационные, яркостные, цветовые; принцип действия.