Выбор вида тенденции
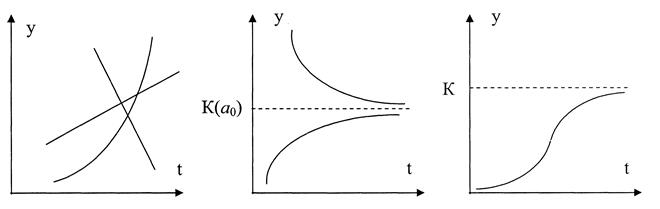
Выбор вида тенденции на основе качественного анализа.Социально-экономические процессы в зависимости от характера их протекания можно разделить на три класса (рис. 16.2):
I) Процессы с монотонным характером развития и отсутствием пределов роста (рис. 16.2, а). Эти условия справедливы для поведения многих экономических показателей, например, для большинства натуральных показателей промышленного производства. В этом случае для моделирования тенденции могут использоваться: линейная 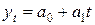 , параболическая
, параболическая 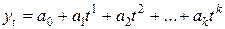 , экспоненциальная
, экспоненциальная  , степенная
, степенная 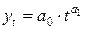 функции.
функции.
 а)I класс б)II класс в)III класс
а)I класс б)II класс в)III класс
Рис. 16.2. Схемы протекания процессов
II) Процессы, которые имеют предел роста (падения) в исследуемом периоде, так называемые процессы с «насыщением» (рис. 16.2, б). Развитие процесса происходит под влиянием некоторых ограничивающих факторов, величина воздействия которых растет вместе с ростом достигнутого уровня. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности использования ресурсов и т. д. Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление определенных продуктов питания, расход удобрений на единицу площади и т.п.
В этом случае для моделирования тенденции используются гиперболическая функция  либо модифицированная экспонента
либо модифицированная экспонента 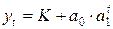 с параметром
с параметром 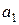 ,удовлетворяющим условию
,удовлетворяющим условию 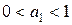 .
.
В случае гиперболы параметр 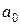 равен пределу роста, к которому значение уровня процесса приближается (при росте t)снизу в случае
равен пределу роста, к которому значение уровня процесса приближается (при росте t)снизу в случае 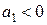 , либо сверху при
, либо сверху при 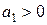 (рис. 16.2 б).
(рис. 16.2 б).
В случае модифицированной экспоненты параметр 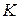 равен пределу роста, к которому значение уровня процесса приближается (при росте t)снизу в случае
равен пределу роста, к которому значение уровня процесса приближается (при росте t)снизу в случае 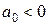 , либо сверху при
, либо сверху при 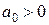 (рис. 16.2, б).
(рис. 16.2, б).
При решении экономических задач часто можно определить значение предела роста исходя из свойств прогнозируемого процесса (например, коэффициент использования оборудования не может превышать 1 и т.п.). Иногда значение предела роста задается экспертным путем.
III) Так называемые S-образные процессы (рис. 16.2, в), представляющие как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, а другой – с замедлением. С такими процессами часто сталкиваются в демографических исследованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.
К S-образным процессам можно отнести процесс развитие новой отрасли (нового производства). Вначале производство развивается очень медленно вследствие того, что технические методы производства еще недостаточно разработаны, издержки производства высоки и спрос на рынке на данный товар еще очень мал, поэтому производство развивается медленно. В дальнейшем, благодаря усовершенствованию технических методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара производство растет быстрее. Затем наступает период насыщения рынка, рост производства все более замедляется, и, наконец, почти прекращается. Наступает стабилизация производства на определенном уровне. Следует отметить, что выявленные закономерности развития следует обобщать с определенной осторожностью и, причем, только для достаточно коротких периодов, так как выявленная тенденция развития производства может быть нарушена вследствие внешних факторов, например, технического переворота в данной отрасли или связанных с нею.
Для моделирования тенденции S-образных процессов следует использовать либо логистическую функцию 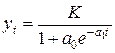 (с параметром
(с параметром 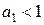 ), либо кривую Гомперца
), либо кривую Гомперца 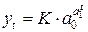 с параметрами, удовлетворяющими условиям
с параметрами, удовлетворяющими условиям  ,
, 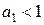 . Предел роста в обоих случаях равен параметру
. Предел роста в обоих случаях равен параметру 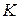 .
.
Выбор вида тенденции на основе анализа показателей динамики временного ряда.Исследуя последовательные разности уровней ряда 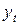 первого, второго и следующих порядков
первого, второго и следующих порядков
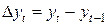 – последовательные разности первого порядка,
– последовательные разности первого порядка,
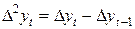 – последовательные разности второго порядка и т.д.,
– последовательные разности второго порядка и т.д.,
можно сделать вывод о наличии тенденции, описываемой полиномиальной функцией от времени t.
Если исходный временной ряд содержит тенденцию, а временной ряд последовательных разностей первого порядка не содержит тенденцию, то можно сделать вывод, что тенденция линейно зависит от времени 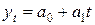 . Коэффициент
. Коэффициент 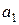 в данном случае численно равен среднему абсолютному приросту уровня явления за единицу измерения временного параметра
в данном случае численно равен среднему абсолютному приросту уровня явления за единицу измерения временного параметра 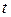 (за сутки, неделю, месяц, год и т.д.).
(за сутки, неделю, месяц, год и т.д.).
Если исходный временной ряд и временной ряд последовательных разностей первого порядка содержат тенденцию, а временной ряд последовательных разностей второго порядка не содержит тенденцию, то можно сделать вывод, что тенденция задается полиномом второго порядка от времени  . Относительно тенденции в виде полинома от t более высокой степени вывод делается аналогично.
. Относительно тенденции в виде полинома от t более высокой степени вывод делается аналогично.
Исследуя отношения последовательных уровней ряда (цепные коэффициенты роста)  ,можно сделать вывод о наличии тенденции, задаваемой экспоненциальной функцией от времени t.
,можно сделать вывод о наличии тенденции, задаваемой экспоненциальной функцией от времени t.
Если исходный временной ряд содержит тенденцию, а временной ряд коэффициентов роста не содержит тенденцию, то можно сделать вывод, что тенденция экспоненциально зависит от времени. Иными словами, тенденция имеет
вид экспоненциальной функции 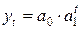 .Величина
.Величина 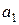 в данном случае численно равна среднему коэффициенту роста уровня явления за единицу измерения временного параметра t (за сутки, неделю, месяц, год и т.д.).
в данном случае численно равна среднему коэффициенту роста уровня явления за единицу измерения временного параметра t (за сутки, неделю, месяц, год и т.д.).
Аналогичный результат можно получить, анализируя первые последовательные разности временного ряда, составленного из логарифмов от исходных уровней.
Если наблюдается линейная зависимость между логарифмами уровней ряда 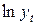 и соответствующих промежутков времени
и соответствующих промежутков времени 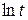 , то рекомендуется использовать степенную функцию
, то рекомендуется использовать степенную функцию 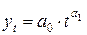 .
.
Дата добавления: 2015-11-06; просмотров: 1819;
