Теплопроводность гетерогенных систем
В строительном материаловедении теплопроводность λ учитывается при расчете ограждающих конструкций для обеспечения:
- тепловой изоляции зданий и сооружений
- тепловой защиты поверхностей тепловых агрегатов и трубопроводов;
- термостойкости огнеупорных материалов и специальных составов;
- хладоизоляции.
Поскольку ограждающие конструкции по своему назначению многофункциональны, составляющие их материалы, как правило, являются гетерогенными пористыми телами. Общая, или эффективная теплопроводность таких систем определяется теплопроводностями твердых и газовых фаз:
λ = λтв + λгаз
Однако, учитывая тот факт, что теплопроводность является векторной величиной, ее суммарное значение для гетерогенных систем зависит не только от количественного соотношения фаз, но и от их взаимного расположения, характера пограничного слоя, степени непрерывности или дискретности фаз и т.д., т.е. от структуры и текстуры материала.
Чтобы оценить эффективную теплопроводность системы, рассмотрим влияние каждой составляющей.
Для оценки зависимости теплопроводности системы от сочетания твердых фаз приведем в качестве примера три упрощенных варианта сочетания твердых фаз двухфазной системы:
- параллельное расположение слоев (фаз), свойственное слоистой структуре материалов (рис.4.4, а);
- основная фаза является непрерывной, а другая - в виде отдельных включений, что соответствует структуре стеклокристаллических материалов (рис.4.4. б);
- основная фаза является дискретной, соответствует структуре, подобной конгломератам, например бетонам, (рис.4.4. в).
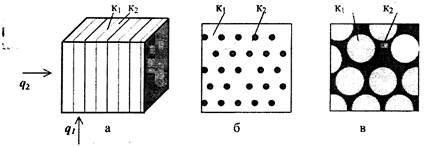
Рис. 4.4. Схемы распределения фаз:
а - параллельными слоями; б - с непрерывной основной фазой;
в - с дискретной основной фазой; к1 - основная фаза, к2 - вторая фаза;
q1, q2 - направления теплового потока
Вариант 1 Слоистая структура (см. рис. 4.4. а)
Если тепловой поток q направлен вдоль слоев, то λ рассчитывается так же, как и электропроводность цепи с параллельно включенными сопротивлениями. При одинаковом ΔТ во всех слоях большая часть тепла переносится через фазу с более высокой теплопроводностью. Среднюю теплопроводность можно рассчитать по формуле:
λср = V1 λ1 + V2 / λ2
где V1 и V2 — объемные доли каждой фазы.
В этом случае общая теплопроводность системы определяется в основном фазой с более высокой теплопроводностью, и если λ1 >> λ2, то λср= V1 λ1.
Если тепловой поток направлен перпендикулярно к плоскости слоев, то имеет место случай, аналогичный случаю электрической цепи с последовательным включением сопротивлений. Тепловой поток, проходящий через все слои, остается величиной постоянной, тогда как ΔТ по слоям различна, и общая теплопроводность определяется соотношением:
1 /λср = V1/λ1 +V2/ λ2 или λср = λ1 λ2/( V1 λ1 + V2 λ2)
В этом случае общая теплопроводность определяется в основном фазой с меньшёй теплопроводностью, и если λ1 >> λ2, то λср~~ λ2/ V2.
Вариант 2. Структура с непрерывной основной фазой (см. рис.4.4. 6).
Если вторая фаза дискретна и по величине не превышает 10%, то общая (средняя) теплопроводность системы определяется теплопроводностью непрерывной фазы.
Вариант З. Структура с дискретной основной фазой (см. рис.4.4. в).
Если содержание второй фазы превышает 10%, то главным фактором, определяющим теплопроводность системы, является соотношение фаз, и условно непрерывной фазой становится большая из них. Общую теплопроводность системы определяют исходя из соотношений Максвелла-Эйкена для непрерывной среды с λ1 и диспергированной в нее фазой с λ2:
Если λ1 >> λ2 , то λср = λ1(1- V2)/(1+ V2).
Если λ1<< λ2, то λср = λ2(1 + 2 V2)/(1 - V2).
Как влияет газовая фаза на теплопроводность системы? Выше упоминалось о том, что гетерогенные системы (неорганические, не металлические материалы), как правило, имеют значительную газовую составляющую, которая колеблется от доли процента у плотных природных каменных материалов до 99% у искусственных полимерных материалов.
Тот факт, что с увеличением газовой фазы или пористости теплопроводность системы уменьшается, не вызывает сомнения. Например, теплопроводность воздуха примерно в 20 раз меньше теплопроводности керамического черепка. Однако необходимо выделить два момента:
- при увеличении пористости теплопроводность системы уменьшается за счет сокращения объема более теплопроводной твердой фазы, что не требует доказательства;
- при увеличении пористости теплопроводность системы снижается еще и за счет уменьшения теплопроводности самой твердой фазы.
Такая закономерность объясняется тем, что поры, образуя новые поверхности в плотной структуре, становятся центрами рассеяния, примерно такими, как дефекты решетки, границы зерен примеси и пр. При этом уменьшается средняя длина свободного пробега частиц и снижается фононная теплопроводность системы.
Если пренебречь влиянием границ зерен и другими факторами, а также теплопроводностью самих пор (т.е. газовой составляющей) и допустить, что поры равномерно распределены в непрерывной среде, то можно получить уравнение Максвелла-Эйкена, показывающее влияние пористости на фононную теплопроводность гетерогенной системы:
λ = λср(1-П)(1+0,5П);
где λ, λср — соответственно теплопроводности системы и твердой фазы в абсолютно плотном состоянии;
П — пористость системы, ед.
Приведенное соотношение теплопроводность — пористость условию для непрерывной твердой фазы с изолированными порами. Однако если непрерывной является газовая фаза, как в порошкообразных и волокнистых материалах, то необходимо учитывать и ее теплопроводность, которая определяется конвективным теплопереносом а, а при температурах выше 600°С — еще и излучением «кч».
При расчете эффективной теплопроводности с учетом конвекции и излучения определяющими факторами являются размер пор и температура. Так, влияние переноса теплоты излучением на теплопроводность пор пропорционально их условному диаметру d и кубу температуры, Следовательно, наличие крупных пор приводит к повышению общей теплопроводности системы, особенно при высокой темпера туре, в то время как мелкие поры являются хорошим препятствием для переноса теплоты.
Следует, однако, снова упомянуть о том, что на теплопроводность влияет не только размер пор, но и непрерывность поровой среды. Причем влияние последнего фактора значительнее.
Из опыта применения высокотемпературной теплоизоляции известно, что в сыпучих и волокнистых материалах, где непрерывной средой является воздух, размер пор, а, следовательно, и размер зерен или толщина волокон практически не оказывают влияния на теплопроводность материалов при низких температурах.
При высоких температурах размер зерен становится значимым параметром, так как с увеличением конвективной составляющей теплопереноса резко возрастает фактор излучения. Поэтому для высокотемпературной изоляции наиболее эффективными являются мелкозернистые или мелкопористые материалы. Теплопроводность же самой твердой фазы или зерна в данном случае имеет второстепенное значение.
При высоких температурах размер зерен становится значимым параметром, так как с увеличением конвективной составляющей теплопереноса резко возрастает фактор излучения. Поэтому для высокотемпературной изоляции наиболее эффективными являются мелкозернистые или мелкопористые материалы. Теплопроводность же самой твердой фазы или зерна в данном случае имеет второстепенное значение.
Дата добавления: 2015-11-06; просмотров: 2062;
