Потенциальная энергия упруго деформированного тела.
Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).
Определим работу, которую необходимо затратить для растяжения (или сжатия) пружины на величину «x» (рис.3.8). Будем считать, что пружина подчиняется закону Гука, т.е. упругая сила пропорциональна деформации. Будем проводить растяжение пружины очень медленно, чтобы силу 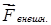 , с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе
, с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе 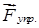 . Далее будем считать, что сила действует в направлении перемещения, т.е.
. Далее будем считать, что сила действует в направлении перемещения, т.е. 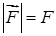 .
.
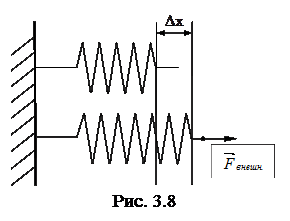 Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).
Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).
Пусть под действием силы 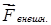 пружина растянулась на dx, тогда dA=F·dx=k·x·dx.
пружина растянулась на dx, тогда dA=F·dx=k·x·dx.
Отсюда
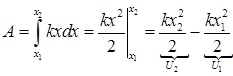 ;
;
Эта работа идет на увеличение потенциальной энергии пружины. В предположении, что потенциальная энергия недеформированной пружины равна «0» (U1 = 0) получаем
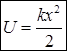 (3.12)
(3.12)
– потенциальная энергия упругой деформации пружины.
| ЛЕКЦИЯ 5 |
Дата добавления: 2015-11-04; просмотров: 977;
