Потенциальная энергия в гравитационном поле (в поле всемирного тяготения).
Установленный Ньютоном закон всемирного тяготения гласит:
ОПРЕДЕЛЕНИЕ: Гравитационная сила или сила тяготения – это сила, с которой две материальные точки притягивают друг друга, пропорциональная массам этих точек и обратно пропорциональная квадрату расстояния между ними 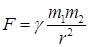 , где g – гравитационная постоянная. Эта сила направлена вдоль прямой, проходящей через взаимодействующие материальные точки.
, где g – гравитационная постоянная. Эта сила направлена вдоль прямой, проходящей через взаимодействующие материальные точки.
Рассмотрим два тела массами m1, m2 (считаем их материальными точками) и будем их сближать от расстояния r1 до r2.
Элементарная работа на пути dr будет 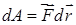 . Полная работа
. Полная работа
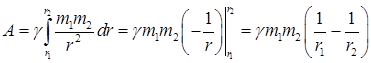 .
.
Т.е. 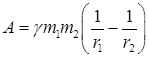 . Величина
. Величина
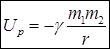 (3.11)
(3.11)
называется потенциальной энергией тела в поле всемирного тяготения.
Если между телами действует сила притяжения, то Up<0;
если между телами действует сила отталкивания, то Up>0.
Из выражения (3.11) следует, что максимальное значение потенциальной энергии тяготеющие тела будут иметь тогда, когда они бесконечно (r = ¥) удалены друг от друга (Up = 0).
Введем величину называемую потенциалом гравитационного поля.
ОПРЕДЕЛЕНИЕ: Потенциал – это скалярная величина, численно равная работе по перемещению в гравитационном поле тела единичной массы из данной точки поля на бесконечность (r=¥).
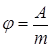 ;
; 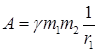 или
или 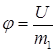 . Поле можно характеризовать потенциальной энергией, которой обладает в данном месте материальная точка.
. Поле можно характеризовать потенциальной энергией, которой обладает в данном месте материальная точка.
Получаем, что 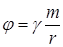 . Зная потенциал, можно вычислить работу, совершаемую над частицей массой «m» силами поля при перемещении ее из положения 1 в положение 2:
. Зная потенциал, можно вычислить работу, совершаемую над частицей массой «m» силами поля при перемещении ее из положения 1 в положение 2: 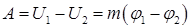 .
.
В потенциальном поле можно провести поверхность, имеющую одинаковый потенциал. Такая поверхность называется эквипотенциальной.
Дата добавления: 2015-11-04; просмотров: 1385;
