Определение допустимых размеров обнажений. Поддержание выработанного пространства магазинированной рудой

На устойчивость обнажений горных пород влияют следующие факторы:

- свойства массива горных пород;

- глубина разработки;

- угол наклона обнажения;

- время стояния обнажения;

- условия, от которых зависит, какая часть толщи пород оказывает давления на обнаженный массив (в долях единиц).

Оценка размеров обнажения:

Доказано, что устойчивость обнажения при малой его длине (l >двойной ширины) зависит от его S (площади).

При большой длине (l >двойной ширины) зависит только от его ширины, а сама длина и S уже не играют роли.

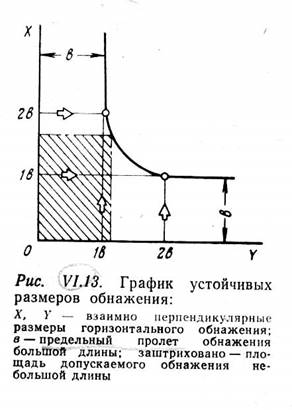
Если l, b и S соответственно длина, ширина (пролет) и площадь кровли, то условия устойчивости обнажения будет:

При l<2b l x b<S_пред

При l>2b b ≤ b_пред

Величину обнажения с точки зрения устойчивости принято характеризовать эквивалентным проектом обнажения (b_э), который определяется так:

При l<2b b_э =b

При l>2в

Предельный эквивалентный пролет обнажения (выше которого наступают разрушения) обозначим b_пред. Тогда условия устойчивости обнажения выразится так: b_э≤b_пред.

Для расчетов предельных пролетов камер применяются методы строительной механики, рассматривающие кровлю как упруго-пластическую среду.

Расчеты слоистой кровли камер по теории В.Д. Слесарева выполняются при следующих допущениях:

· обнаженная кровля выработки подобна свободно опертой или защемленной плите;

· расчет плиты можно заменить расчетом эквивалентной балки;

· плиты и балка будут испытывать приблизительно одинаковое напряженно-деформированное состояние в наиболее опасных сечениях, если их гидравлические радиусы равны;

· всякую выработку, ограниченную по контуру, можно заменить эквивалентной выработкой бесконечно большой длины, кровля которой будет испытывать такие же напряжения и деформации, как и кровля камеры;

· для расчета однопролетной балки, эквивалентной кровле горной выработки, можно использовать графический способ построения кривой давления, который применяется в статике сооружения для расчета сводов;

· кровля горных выработок работает за пределами упругих и упруго-пластических деформаций (до момента потери его устойчивости).

Под гидравлическим радиусом понимается отношение площади обнажения камеры S к ее периметру Р, т. е.

где a и b – соответственно ширина и длина камеры.

Заменяя для расчета плиту эквивалентной балкой, можно определить гидравлический радиус выработки бесконечной длины

Отсюда следует, что эквивалентный пролет камерной выработки . Поэтому при расчетах кровли камеры необходимо принимать балку с эквивалентным пролетом.

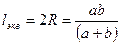
Работу кровли В.Д. Слесарев предлагает рассматривать в трех состояниях, которые он назвал предельными (см. табл.)

Предельные состояния слоистой кровли

Предельное состояние кровли	Характеристика состояния кровли	Предельные пролеты балки
Свободно опертой	С защемленными концами
I	В кровле отсутствуют растягивающие напряжения
II	Породы кровли испытывают максимальные деформации (прогиб) без нарушения сплошности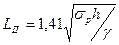
Появляются трещины и возможно частичное обрушение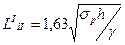
III	Трещины распространяются на всю мощность кровли, и она обрушается

На практике наибольшее распространение получил метод расчета по теории тонких плит при соотношении от h/l≥1/5 до h/l≥1/3, где h – толщина плиты, l – ширина плиты (камеры).

Для кровли, сложенной однородными трещиноватыми породами, величина устойчивого пролета для одного слоя определяется из зависимости

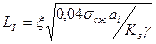
где ξ – коэффициент ползучести породы при сжатии, ξ=0,5-0,7; a_i - расстояние между трещинами в направлении, нормальном к поверхностям системы трещин наибольшего ослабления (толщина слоя, пролет которого определяется); K_з – запас несущей способности породного слоя (рекомендуется К_з =4)

С учетом угла наклона трещин наибольшего ослабления или падения слоев а предельный пролет определим из выражения

Эти формулы справедливы при условии, когда a_i/L_i≤1/5 и a_i>0,25, а слой породы, устойчивый пролет которого определяется, не нагружен весом вышележащей толщи пород.

Исследованиями отечественных ученых теория В.Д. Слесарева была развита в дальнейшем (С.Г. Авершин, Г.Н. Кузнецов, А.А. Борисов, С.В. Ветров и др.). Разработан ряд методик расчета устойчивых пролетов для различных условий. Рассмотрим некоторые из них.

По методике ВНИМИ для пологих залежей, допустимый пролет для камер с прямоуголь­ным контуром обнажения для слоистых кровель определяется из выраже­ния:

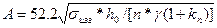, м

где: s_изг - предел прочности нижнего несущего слоя кровли при из­гибе, МПа, s_изг=(2...5)s_раст; h_о - мощность нижнего несущего слоя, м; n - ко­эффициент запаса прочности, n=2...4; g - средний объемный вес пород кровли, кН/м³; k_п - коэффициент пригрузки нижнего несущего слоя весом налегающих пород, зависит от соотношения мощности нижнего несу­щего слоя h₀ и глубины разработки Н, при h_о/H<0.1 k_п =0.7; при 0.1<h_о/H<0.3 k_п =0.4-0.6; при 0.3<h_о/H<0.5 k_п =0.3-0.4; при 0.5<h_о/H<1 k_п=0.2; при h_о/Н=1 k_п =0.

Для горизонтальных и пологих залежей при однородной кровле и от­ношении глубины заложения камеры к ее ширине более двух, коэффици­ента Пуассона m =0.17-0.3, допустимый пролет обнажения можно опре­делить по формуле С.Г.Борисенко:

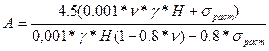, м

где: » 0.2 - 0.4 - коэффициент бокового распора;

s_раст - допустимое напряжение при растяжении для пород кровли, МПа.

Фактический пролет камеры принимают по конструктивным сообра­жениям с учетом применяемой техники и технологии, при этом он не должен превышать рассчитанный допустимый пролет обнажения, т.е. А< А _д.

Для определения допустимых пролетов обнажения при крутом паде­нии залежи рекомендуется использовать зависимости для расчета допус­тимых эквивалентных обнажений в камерных системах разработки (методика НИГРИ). Ус­тойчивость обнажений, рассчитанных по этим зависимостям, обеспечи­вается в течении 6 месяцев.

Для наклонных обнажений эквивалентный пролет определяется по формуле:

, м,

где: б_сж - предел прочности материала обнажения при сжатии, МПа; g - объемный вес налегающих пород, кН/м³; H - глубина заложе­ния камер от поверхности, м; n - коэффициент запаса прочности.

Для вертикальных обнажений:

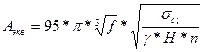, м,

где: f - коэффициент крепости.

Для перехода от величин эквивалентных пролетов к реальным раз­мерам камер можно воспользоваться формулой В.Д.Слесарева для выра­боток с прямоугольным опорным контуром:

A_экв = 2*S/P,

где: S - площадь обнажения, м²; P - периметр обнажения, м.