Определение деформаций балок переменного сечения.
При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид
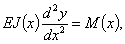
где J(x) — переменный момент инерции сечений балки.
До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует 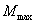 ; после этого вычисления производятся так же, как и.для балок постоянного сечения.
; после этого вычисления производятся так же, как и.для балок постоянного сечения.
Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.
Тогда
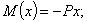
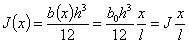

Дифференциальное уравнение принимает вид:
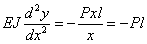
Интегрируем два раза:
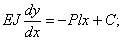
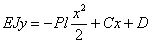
Для определения постоянных интегрирования имеем условия: точке А при 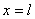 прогиб
прогиб 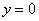 и угол поворота
и угол поворота 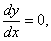 или
или
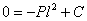 и
и 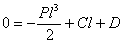
отсюда
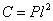 и
и 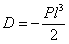
Выражения для у и 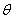 принимают вид;
принимают вид;
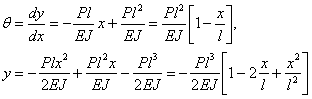
Наибольший прогиб на свободном конце балки В получится при 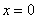 : он равен
: он равен
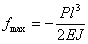
Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы
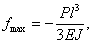
т. е. в 1 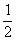 раза меньше.
раза меньше.
Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.
Дата добавления: 2015-10-26; просмотров: 610;
